Free Software Development.
3. Numerical Description of Weak Acid with Weak Base Titration
Lorentz JÄNTSCHI*, Horea Iustin NAŞCU
Technical University Cluj-Napoca
*http://lori.academicdirect.ro
Abstract
The analytical methods of qualitative and quantitative determination of ions in solutions are very flexible to automation.
The present work is focus on modeling the process of titration and presents a numerical simulation of acid-base titration.
A PHP program to compute all iterations in titration process that solves a 3th rank equation to find value of pH for was built and is available through http internet protocol at the address:
http://vl.academicdirect.org/molecular_dynamics/ab_titrations/v1.1/
The method allows expressing the value of pH in any point of titration process and permits to observe the equivalence point of titration.
Keywords
Titration, Acid-base reactions, Simulation, Mathematical modeling of chemical processes, Server side processing.
1. Introduction
The process of titration is a recurrent process that can be watched by permanent measurement of a simple property such as mass, current intensity, tension, volume [1]-[3] or a complex property such as adsorption, heat of reaction [4]-[6], which need a complex evaluation.
Currently, is sent over the two milliards of probes to laboratories of medical clinics and this number growing. Most of these tests include the determination of glucose, urea, proteins, sodium, calcium, HCO3-/H2CO3, uric acid and pH [7]-[9].
The science of environment are focused on chemical, physical and biological changes through contaminating or modifying natural parameters of air, water, soil, alimentary products and residues [10]-[12].
The analysis of these can give the measure of human provoked modifications and can indicate the conditions that make them possible. Thus, the applying of science and technology can control and ameliorate the quality of environment.
2. Analytical Measurements
Any simple or complex the measurements can be, the assurance, utility, precision, interpretation and achievement of them depend of the analyst, that must be preoccupied -by making analysis and in same time by the how - why and where are the finally results of analysis used.
The analyst has the obligation to make determination based on sure, reproducible and verified procedures.
The first step in design of an analytical process is to establish the objective to follow.
Only by clear identification of proposed scope it can imagined a logic way that lead to correct solving of the problem [13],[14].
A big responsibility for the analyst is to choose an analytical method that is leading to best solving of followed scope [15].
There exist cases when freedom of choosing is limited. The analysis of water or pharmaceuticals must make through legal standard approved procedures [16].
If more than one similarly probe exists, such as quality control, the automation becomes possible [17].
3. Neutralization
An easy way to make an analytical method for quantitative determinations is trespassing from an acid solution to a basic one, known as neutralization.
In this case, evolution of reaction can be watched through pH measurements, continuously, when a known volume of titrating solution is added.
Usually, a strong acid or a strong base is solution added, but in biochemical processes, most of the acids and bases are weak. This is the reason for chousing a weak acid and a weak base for titration modeling.
The plot of the pH as function of added standardized solution is the titration curve. Many data result from a titration curve.
Most important for the quantitative determinations is volume of titrating solution necessary for neutralization (pH = pOH = 7 at 25°C) [18].
4. Reaction Modeling
A weak acid titration with a weak base can be expressed by the equation:
HA + BOH ![]() AB + H2O (1)
AB + H2O (1)
If the titration is made in water, must be considered also the dissociation of water:
HOH ![]() HO- + H+ (2)
HO- + H+ (2)
The processes of acid and base dissociation are:
HA ![]() H+ + A- (3)
H+ + A- (3)
BOH ![]() B+ + HO- (4)
B+ + HO- (4)
Also, salt are in equilibrium with his ions:
AB ![]() A- + B+ (5)
A- + B+ (5)
The titration starts with adding of a small quantity of base in acid. In solution are present the species H+, HO-, HA and A-. From acid dissociation (equation 3) it result:
[H+]∙[A-] = Ka∙[HA] (6)
and from water dissociation (equation 2):
[H+]∙[HO-] = Kw (7)
where [∙] is the molar concentration operator ([H+] is the molar concentration), Ka is acidity constant and Kw is water constant of dissociation. If are applied the mass balance for the acid (see equations 3-5), it results:
Ca = [HA] + [H+] – [HO-] (8)
where Ca is analytical concentration of the acid.
If are applied the mass balance for the salt, it results:
Cs = [A-] – [H+] + [HO-] (9)
where Cs is analytical concentration of the salt.
With proper substitutions a 3th rank equation of pH are obtained (Brönsted equation):
x3 + (Ka+Cs)*x2 - (Kw+Cx*Ka)*x - Kw*Ka = 0 (10)
where x = [H+].
The equation (10) has a unique solution in (0,1) interval and note that:
Cs = Cb*Vx/(Va+Vx) (11)
Cx = (Ca*Va-Cb*Vx)/(Va+Vx) (12)
where Cb is analytical concentration of the base, Vx is added volume of base, Cx is analytical concentration of acid after adding of Vx volume of base and Va is initial volume of acid.
The equation (10) with substitutions (11) and (12) can be solved numerically.
At equivalence point, all (1-4) equations must be considered. With an small hydrolysis Cs = [B+] = [A-] and:
x = 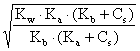 (13)
(13)
With a similar deduction, the equation of [H+] is given by:
x3+(Kw/Kb+Cx)*x2-(Kw+Cs*Kw/Kb)*x-Kw2/Kb = 0 (14)
where the expressions of Cx (base excess) and Cs are:
Cx = (Cb*Vx-Ca*Va)/(Va+Vx) (15)
Cs = Ca*Va/(Va+Vx) (16)
For obtaining a concrete model of titration, let consider the case of NH3 (kb = 1.79∙10-5) solution titrate with CH3COOH (ka = 1.76∙10-5). Remark that NH3 is a typically weak base and CH3COOH is a typically weak acid.
5. Program Projecting
Once you have an operating system installed, the next step is to choose a proper programming language for software developing.
In terms of programming, portability of resulted program can be a problem. As example, if we are chose to implement the algorithm in Visual Basic, the execution of the program is restricted to Windows machines. If Perl is our choice, a Unix-based machine is necessary to run program. If we chouse to implement the program in C language, we will have serious difficulties to compile the programs on machines running with different operating systems. The complexity of program building is also a serious reason in language chousing. Is known that C based languages is poor in simplicity and necessity more time to expend for application building than other languages.
Other question require an answer: We want a server-based application or client based application, a server side application or a client side application.
As example, a client side application can have disadvantage of execution on client, and dependence of processing speed by power of client machine. If we prefer this variant, a java script or visual basic script is our programming language.
A server side application requires a web server installed. The area of web servers is also a large set, but few have multiplatform capability. If we want a full featured web server, Apache is our solution [19].
Under Apache, we have the possibility to execute programs already compiled in C, Fortran and Java, under Unix machines we can directly execute Perl programs, and, most important, under all operating system platforms we can execute PHP programs if we previously install php language and module binaries [20].
The advantage of PHP programs consist in his portability under most of operating system platforms and internal compilation feature that do not necessity the compilation “by hand” from the user. The disadvantage can be same internal compilation that consumes supplementary time in execution. But, this disadvantage can be partially eliminated through installing a PHP proxy, that store compiled programs and next execution of the unmodified program use this compiled binary. In terms of program developing PHP is easy to use, the language borrow syntax from C, Pascal, Basic and Perl, but do not borrow the complex declaration syntax from them. The pointer mechanism is absolute. Thus, a variable used as a string, can be exploited as an integer or real if the value represent a number such that. Class constructing is also available and PHP posses a strong library of database connectivity. Modular programming, recursivity and graphics are at home! Module loading of compiled programs in other languages and execution of binary programs is also available. System services such as mail service are easy to exploit in PHP scripts. A very easy mechanism to link PHP scripts to HTML scripts make PHP language to be one of the best. Shell executing commands make PHP a useful platform for system administration (PhpSysInfo, WebAdmin, PhpMyAdmin, PhpPgAdmin) [21]. As a conclusion, PHP is our choice!
6. Program Implementation
An html form interface for chousing acid, base, adding quantity, volumes, and concentrations allow user to select a weak acid and a weak base (fig. 1).
The user select desired options and press submit button (Make) to send data through a post method to titration.php located in same directory. For substances, values that are sending are constants of equilibrium.
The titration.php program computes iteratively for every added quantity of base the coefficients for equation (10) until the equilibrium is reached and then calculates pH through relation (13) and after that computes iteratively the coefficients for equation (14). For every case of coefficients determination (equations 10 and 13) the third rank equation is solved searching the solution by halving the current interval starting with [0, 1] interval (that correspond to a real value of pH) until the difference are analytically insignificant (four digits) [22].
|
Acid: |
|
Quantity:
|
|
Concentration: |
|
|
Base: |
|
Quantity: |
|
Concentration: |
|
|
Adding quantity: |
|
|
|
||
Fig. 1. index.php program
The resulted values of pH for every added quantity of base are tabulated and send to the client (user). The values can now be exported to any table-based program to make graphics.
7. Applications
The index.php and titration.php programs are consecutively runs for different acids and bases, and the results are plotted in following figures for the values Ca=Cb=0.01 M; Vb=2∙Va=20 ml; Vx=x∙0.1 ml; x=0..200 it result:
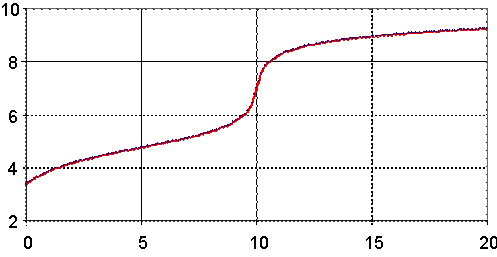
Fig. 2. pH = pH(Vx) for Ka = 1.76∙10-5 (HAc), Kb = 1.79∙10-5 (NH3)
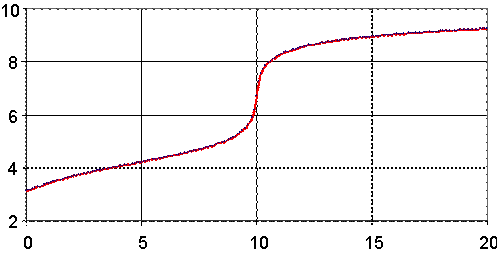
Fig. 3. pH = pH(Vx) for Ka = 6.3∙10-5 (ArCOOH), Kb = 1.79∙10-5 (NH3)
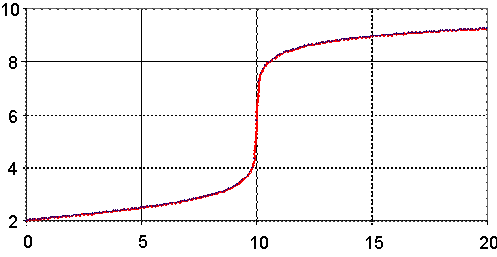
Fig. 4. pH = pH(Vx) for Ka = 4.2∙10-1 (Picric acid), Kb = 1.79∙10-5 (NH3)
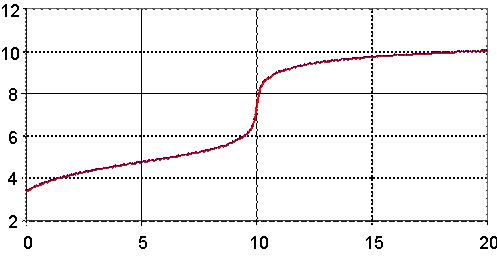
Fig. 5. pH = pH(Vx) for Ka = 1.76∙10-5 (AcCOOH), Kb = 1.1∙10-4 (AgOH)
5. Conclusions and Remarks
Looking at the figures (fig. 2, as example), we can observe the variation of dependency through process.
First, variation is faster, because does not exist enough salt formed to create salt-acid tampon solution.
Second, the variation of the pH is higher until the equivalence point than after the equivalence point, because before equivalence point, forming of salt is continuous and formation of salt increase tampon strength (see fig. 6).
The titration process is simple in appearance but shows to be complex in details. Even the simple case of titration of monobasic base ammonia with a mono-protic acid, such as acetic acid, we must manipulate complex equations (like 10 and 13).
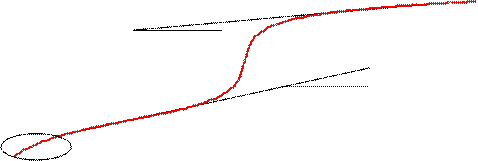
Fig. 6. Analysis of a titration curve
The method allows investigating more complex processes such as reaction of poly-acids with poly-bases. If no approximation will be made, equations that are more complex will be necessary and superior rank equations will appear to be solved [23].
Anyway, the advantages of the method are higher than disadvantages resulted from complexity of calculus. Lack of approximations permits to express pH in all domain points with maximum accuracy.
References