Data Mining. 1.
Glycine Content Estimation from Activity Coefficients Measurement
Lorentz JÄNTSCHIa, Mircea V. DIUDEAb
a Technical University of Cluj-Napoca, RO, http://lori.academicdirect.ro
b "Babeş-Bolyai" University of Cluj-Napoca, RO, http://j.academicdirect.ro/~diudea
Abstract
The paper presents a method to estimate the glycine content from salt aqueous solutions based on standard adding of salt repeated activity coefficients measurement. An original program for data mining is presented. The program execution shows that the glycine content can be predicted from mean ionic activity coefficients in the presence of glycine at room chamber temperature.
The original program was build up on PHP technology and can run via HTTP service at the address:
http://academicdirect.ro/virtual_library/molecular_topology/data_mining/
Keywords
Data mining, PHP programming, QSPR/QSAR studies
Introduction
The software market provides a varied offer for data mining and analysis. Beginning with office software like Microsoft Excel [1] and ending with professional data mining software like StatSoft Statistica [2] a large list of choices and modalities to mining data are available. Even if the software pool is sometimes endless, it does not offer a complete answer on data dependency. In a previous paper [3], it was discussed a program capable to consider all possible dependencies in a data set and to generate a complete list of data predictors. The program was adapted now to store results into a database; by querying the database is now possible to obtain the best predictor of selected variable.
Note that the actual program does not replace the old one in tasks. First, located at the address
http://vl.academicdirect.ro/applied_statistics/linear_regression/multiple/v1.5/
it makes all recursively combinations to find dependencies. The present one considers only a user selection subset of the data set, the results being used for prediction, validation and comparison.
Program Interface and Architecture
The program has two interfaces: the first one (figure 1) is for query statistics and allows user to enounce a SQL query for `statistics` table interrogation.
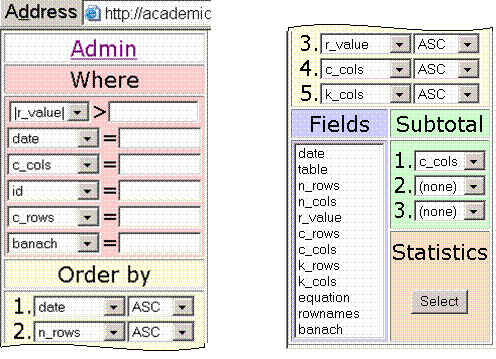
Fig. 1. Query statistics menu of data_mining program
First, the user selects his fields and the order (by clauses) of subtotal statistics, by pressing the Select button; the query is thus made.
The second menu interface is available from Admin link and leads to (figure 2):
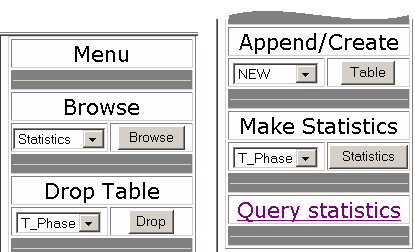
Fig. 2. Operations menu of the data mining program
Note that the access to the operations menu is password restricted, by data security reasons. First step of data analysis is data submitting to server, via append/create option (figure 3):
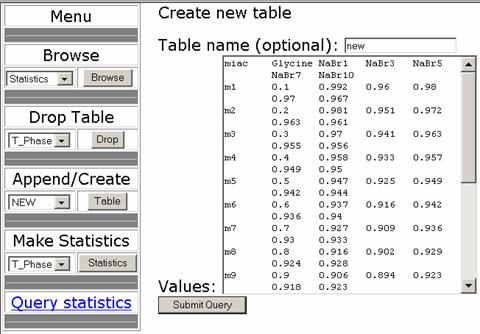
Fig. 3. Data uploading (data_mining program)
The data must be in table format, with columns, rows and captions included. The submitted data are stored into a MySQL table with the same names as gives by the user.
After uploading, the table will appear in table’s lists. The user can browse or drop the table and, most important, can make statistics on it.
First step in statistics making is to select a subset of data (figure 4).
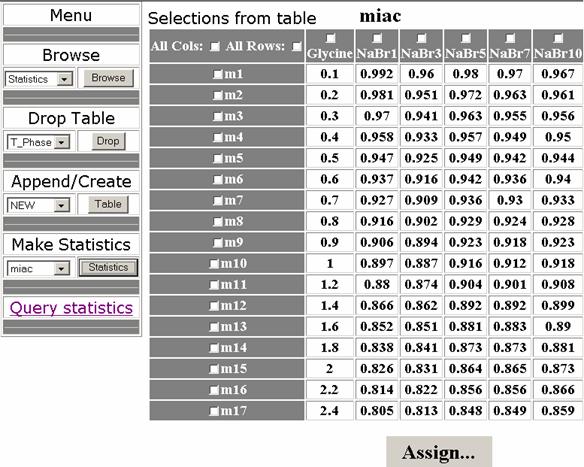
Fig. 4. Data selecting (data_mining program)
Based on user selection, the program displays selected values (figure 5) and allows user to select the dependent and independent variables (X for independent, Y for dependent ones). Further, Rnd check box enables, for the selected variable(s), a test of significance or validation, by permuting values into a column.
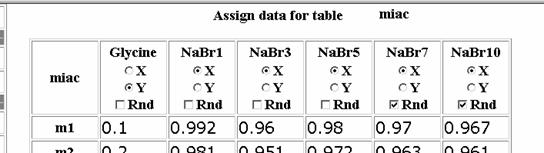
Fig. 5. Data assigning (data_mining program)
In the same window (figure 6), after the data assignment, the user must select the required threshold for the correlation coefficient r. If the user wants to convert the data to a Banach Space [4], he submits them to the partial least squares coefficients determination procedure [5].
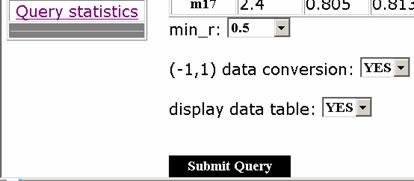
Fig. 6. Limits and conversion features (data_mining program)
All statistics results are written into a `statistics` table with the structure given below.
|
c_cols |
date |
table |
n_rows |
n_cols |
r_value |
c_rows |
k_rows |
k_cols |
equation |
rownames |
banach |
id |
In the above, `c_cols` column stores the name of permuted values column (if any) or "Y" value otherwise and allows to select a specific subset of correlation data, according to the permuted column (Rnd option). The `date` column stores the date in format YY:MM:DD:HH:mm:SS (Y-year, M-month, D-day, H-hour, m-minute, s-second, e.g., 03:10:01:18:13:49). The `table` column stores the name of original table, from which a subset was extracted. The `n_rows` and `n_cols` store the number of data rows and columns (excepting the subtotal records, for which the fields is empty). The `r_value` column stores the correlation coefficient founds. The `c_rows` contain the name of starting row in rows permutation (if any), empty (for subtotals) or null (for non-permuted data). The `k_rows` contain an ordered list of all considered rows, stored by their record numbers. The `k_cols` is the place for selected columns. The `equation` field contains the regression equation as a string (in our case, a value is given in eq. 1. The `rownames` field stores an ordered list of names for selected rows. Finally, the `banach` field can store only two values (0 or 1), depending on user choice, about the converting data to a Banach Space.
Results and discussion
Using the data_mining program it is easy to discover the dependency between measured or calculated parameters. A set of experimental data [6] (Table 1) was considered for testing the program. The collected data represent the ratio of the mean ionic activity coefficients of NaBr, in the presence of glycine, at different NaBr and glycine molalities, at T = 298.15 K. The NaBrX (X=1, 3, 5, 7, 10) columns contain the activity coeffcients of NaBr solved in ratios of 0.1, 0.3, 0.5, 0.7 and 1.0 mol∙kg-1. For glycine, only molality (in I.S. units) is provided.
Table 1. ratios of the mean ionic activity coefficients of NaBr in the presence of glycine [6]
|
miac |
Glycine |
NaBr1 |
NaBr3 |
NaBr5 |
NaBr7 |
NaBr10 |
|
miac |
Glycine |
NaBr1 |
NaBr3 |
NaBr5 |
NaBr7 |
NaBr10 |
|
m1 |
0.1 |
0.992 |
0.96 |
0.98 |
0.97 |
0.967 |
|
m10 |
1 |
0.897 |
0.887 |
0.916 |
0.912 |
0.918 |
|
m2 |
0.2 |
0.981 |
0.951 |
0.972 |
0.963 |
0.961 |
|
m11 |
1.2 |
0.88 |
0.874 |
0.904 |
0.901 |
0.908 |
|
m3 |
0.3 |
0.97 |
0.941 |
0.963 |
0.955 |
0.956 |
|
m12 |
1.4 |
0.866 |
0.862 |
0.892 |
0.892 |
0.899 |
|
m4 |
0.4 |
0.958 |
0.933 |
0.957 |
0.949 |
0.95 |
|
m13 |
1.6 |
0.852 |
0.851 |
0.881 |
0.883 |
0.89 |
|
m5 |
0.5 |
0.947 |
0.925 |
0.949 |
0.942 |
0.944 |
|
m14 |
1.8 |
0.838 |
0.841 |
0.873 |
0.873 |
0.881 |
|
m6 |
0.6 |
0.937 |
0.916 |
0.942 |
0.936 |
0.94 |
|
m15 |
2 |
0.826 |
0.831 |
0.864 |
0.865 |
0.873 |
|
m7 |
0.7 |
0.927 |
0.909 |
0.936 |
0.93 |
0.933 |
|
m16 |
2.2 |
0.814 |
0.822 |
0.856 |
0.856 |
0.866 |
|
m8 |
0.8 |
0.916 |
0.902 |
0.929 |
0.924 |
0.928 |
|
m17 |
2.4 |
0.805 |
0.813 |
0.848 |
0.849 |
0.859 |
|
m9 |
0.9 |
0.906 |
0.894 |
0.923 |
0.918 |
0.923 |
|
|
|
|
|
|
|
|
The query of `statistics` table on all `miac` selected values shows that the glycine concentration is strongly dependent on NaBr ionic activity (if both exists in solution). The equation that proves this truth is:
YGlycine=21.448XNaBr1-0.232XNaBr3-22.943XNaBr5-27.755XNaBr7+7.884XNaBr10+20.808*1
m = 17; r = 0.998 (1)
The program allows the calculation of monovariate regression (i.e., a single independent variable, e.g., NaBr1):
YGlycine=-11.977*XNaBr1+11.853*1
m = 17; r = 0.992 (2)
Supposing that we want to validate the assumption of NaBr1 dependency, all that we have to do is to include a validation test on NaBr1 variable in our program. This task can be done on two ways (figure 7).
 or
or

Fig. 7. Validation test running (Rnd checkbox selection)
The execution of the program in both cases will produce a set of correlations (figure 8, see also figure 7 for correspondences):
|
YGlycine=-11.9774*XNaBr1+11.8528*1 YGlycine=-7.4288*XNaBr1+7.7558*1 YGlycine=-3.5341*XNaBr1+4.2479*1 YGlycine=-0.2988*XNaBr1+1.3338*1 YGlycine=2.2304*XNaBr1-0.9442*1 YGlycine=4.0916*XNaBr1-2.6206*1 YGlycine=5.3249*XNaBr1-3.7314*1 YGlycine=5.9267*XNaBr1-4.2735*1 YGlycine=5.8571*XNaBr1-4.2108*1 |
|
YGlycine=-11.9774*XNaBr1+11.8528*1 YGlycine=-8.5594*XNaBr1+8.7742*1 YGlycine=-5.3571*XNaBr1+5.8899*1 YGlycine=-2.4992*XNaBr1+3.3157*1 YGlycine=0.0126*XNaBr1+1.0534*1 YGlycine=2.0877*XNaBr1-0.8157*1 YGlycine=3.7193*XNaBr1-2.2853*1 YGlycine=4.9022*XNaBr1-3.3507*1 YGlycine=5.5023*XNaBr1-3.8912*1 |
Fig. 8. Output of validation tests
|
YGlycine=5.5023*XNaBr1-3.8912*1 YGlycine=4.9022*XNaBr1-3.3507*1 YGlycine=3.7193*XNaBr1-2.2853*1 YGlycine=2.0877*XNaBr1-0.8157*1 YGlycine=0.0126*XNaBr1+1.0534*1 YGlycine=-2.4992*XNaBr1+3.3157*1 YGlycine=-5.3571*XNaBr1+5.8899*1 YGlycine=-8.5594*XNaBr1+8.7742*1 YGlycine=-11.9774*XNaBr1+11.8528*1 |
|
YGlycine=5.8571*XNaBr1-4.2108*1 YGlycine=5.9267*XNaBr1-4.2735*1 YGlycine=5.3249*XNaBr1-3.7314*1 YGlycine=4.0916*XNaBr1-2.6206*1 YGlycine=2.2304*XNaBr1-0.9442*1 YGlycine=-0.2988*XNaBr1+1.3338*1 YGlycine=-3.5341*XNaBr1+4.2479*1 YGlycine=-7.4288*XNaBr1+7.7558*1 YGlycine=-11.9774*XNaBr1+11.8528*1 |
Fig. 8. Output of validation tests (continuing)
After the regression validation procedure running, the program put automatically the regression results into the database. A query can be applied now to the database (see also fig 1):
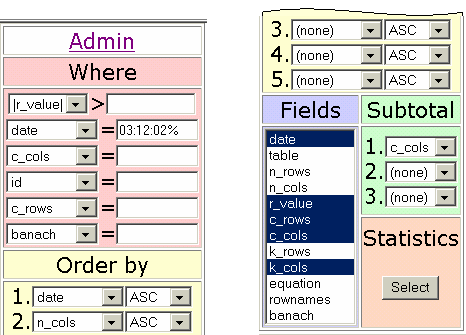
Fig. 9. Query statistics for validation analysis
The query from figure 9 will produce a full analysis of database contents, detailed in figure 10 (a, b and c):
|
c_cols |
date |
r_value |
c_rows |
k_cols |
id |
|
XNaBr1 |
03:12:02:09:12:08 |
0.001 |
m14 |
Glycine.NaBr1 |
79 |
|
XNaBr1 |
03:12:02:09:12:08 |
0.0247 |
m4 |
Glycine.NaBr1 |
69 |
|
XNaBr1 |
03:12:02:09:12:08 |
0.1729 |
m13 |
Glycine.NaBr1 |
78 |
|
XNaBr1 |
03:12:02:09:12:08 |
0.1847 |
m5 |
Glycine.NaBr1 |
70 |
|
XNaBr1 |
03:12:02:09:12:08 |
0.207 |
m15 |
Glycine.NaBr1 |
80 |
|
XNaBr1 |
03:12:02:09:12:08 |
0.2927 |
m3 |
Glycine.NaBr1 |
68 |
|
XNaBr1 |
03:12:02:09:12:08 |
0.308 |
m12 |
Glycine.NaBr1 |
77 |
|
XNaBr1 |
03:12:02:09:12:08 |
0.3389 |
m6 |
Glycine.NaBr1 |
71 |
|
XNaBr1 |
03:12:02:09:12:08 |
0.406 |
m11 |
Glycine.NaBr1 |
76 |
|
XNaBr1 |
03:12:02:09:12:08 |
0.441 |
m7 |
Glycine.NaBr1 |
72 |
|
XNaBr1 |
03:12:02:09:12:08 |
0.4437 |
m16 |
Glycine.NaBr1 |
81 |
|
XNaBr1 |
03:12:02:09:12:08 |
0.4557 |
m10 |
Glycine.NaBr1 |
75 |
|
XNaBr1 |
03:12:02:09:12:08 |
0.4851 |
m9 |
Glycine.NaBr1 |
74 |
|
XNaBr1 |
03:12:02:09:12:08 |
0.4909 |
m8 |
Glycine.NaBr1 |
73 |
|
XNaBr1 |
03:12:02:09:12:08 |
0.6153 |
m2 |
Glycine.NaBr1 |
67 |
|
XNaBr1 |
03:12:02:09:12:08 |
0.709 |
m17 |
Glycine.NaBr1 |
82 |
|
XNaBr1 |
03:12:02:09:12:08 |
0.9921 |
m1 |
Glycine.NaBr1 |
83 |
|
XNaBr1 |
- |
0.3864 |
- |
- |
T(17) |
Fig. 10. (a) Validation statistics for X randomizing (see fig. 7)
|
Y |
03:12:02:09:10:51 |
0.9921 |
0 |
Glycine.NaBr1 |
48 |
|
Y |
03:12:02:09:12:08 |
0.9921 |
0 |
Glycine.NaBr1 |
66 |
|
Y |
- |
0.9921 |
- |
- |
T(2) |
Fig. 10. (b) Validation statistics without randomizing (continuing from figure 10a)
|
YGlycine |
03:12:02:09:10:51 |
0.001 |
m5 |
Glycine.NaBr1 |
52 |
|
YGlycine |
03:12:02:09:10:51 |
0.0247 |
m15 |
Glycine.NaBr1 |
62 |
|
YGlycine |
03:12:02:09:10:51 |
0.1729 |
m6 |
Glycine.NaBr1 |
53 |
|
YGlycine |
03:12:02:09:10:51 |
0.1847 |
m14 |
Glycine.NaBr1 |
61 |
|
YGlycine |
03:12:02:09:10:51 |
0.207 |
m4 |
Glycine.NaBr1 |
51 |
|
YGlycine |
03:12:02:09:10:51 |
0.2927 |
m16 |
Glycine.NaBr1 |
63 |
|
YGlycine |
03:12:02:09:10:51 |
0.308 |
m7 |
Glycine.NaBr1 |
54 |
|
YGlycine |
03:12:02:09:10:51 |
0.3389 |
m13 |
Glycine.NaBr1 |
60 |
|
YGlycine |
03:12:02:09:10:51 |
0.406 |
m8 |
Glycine.NaBr1 |
55 |
|
YGlycine |
03:12:02:09:10:51 |
0.441 |
m12 |
Glycine.NaBr1 |
59 |
|
YGlycine |
03:12:02:09:10:51 |
0.4437 |
m3 |
Glycine.NaBr1 |
50 |
|
YGlycine |
03:12:02:09:10:51 |
0.4557 |
m9 |
Glycine.NaBr1 |
56 |
|
YGlycine |
03:12:02:09:10:51 |
0.4851 |
m10 |
Glycine.NaBr1 |
57 |
|
YGlycine |
03:12:02:09:10:51 |
0.4909 |
m11 |
Glycine.NaBr1 |
58 |
|
YGlycine |
03:12:02:09:10:51 |
0.6153 |
m17 |
Glycine.NaBr1 |
64 |
|
YGlycine |
03:12:02:09:10:51 |
0.709 |
m2 |
Glycine.NaBr1 |
49 |
|
YGlycine |
03:12:02:09:10:51 |
0.9921 |
m1 |
Glycine.NaBr1 |
65 |
|
YGlycine |
- |
0.3864 |
- |
- |
T(17) |
Fig. 10 (c) Validation statistics for Y randomizing (see fig. 7, continuing from figure 10b)
Starting from ionic activity determinations in an unknown glycine concentration solution, a simple regression analysis provides a QSPR (quantitative structure- property relationship) model (eqs 1 or 2). the glycine concentration was determined with two decimals precision in NaBr+Glycine solutions.
The linear dependency between ionic activity and glycine concentration, given by eq 2, can be extended to solutions with unknown concentration of a significant component (say, aminoacid). The experimental part for ionic determination, according to [6], was performed on a Jenway ion analyzer, Model 3045.
Conclusions
The program allows an efficient management of data submitted to a correlation study, with re-viewing and differently selecting subsets.
The multiple subsets selection from inputted data let us to establish more than one QSPR/QSAR relations between data sets, depending on theoretical and/or experimental requests. The friendly interface of data analysis shorts significant the analysis time.
The results storage and data conversion features show the versatility and efficiency of the proposed data mining procedure.
References
The program: