Analytical Study of Oxalates Coprecipitation

Liana MARTA^a, Ossi HOROVITZ^b, Maria ZAHARESCU^c

^a Technical University of Cluj-Napoca, RO

^{b “}Babeş-Bolyai” University, Cluj-Napoca, RO

^c Physical Chemistry Institute of Romanian Academy, Bucharest, RO

Abstract

     The paper deals with the establishing of the oxalates coprecipitation conditions in view of the synthesis of superconducting systems. A systematic analytical study of the oxalates precipitation conditions has been performed, for obtaining superconducting materials, in the Bi Sr-Ca-Cu-O system. For this purpose, the formulae of the precipitates solubility as a function of pH and oxalate excess were established.

The possible formation of hydroxo-complexes and soluble oxalato-complexes was taken into account. A BASIC program was used for tracing the precipitation curves. The curves of the solubility versus pH for different oxalate excess have plotted for the four oxalates, using a logaritmic scale. The optimal conditions for the quantitative oxalate coprecipitation have been deduced from the diagrams. The theoretical curves were confirmed by experimental results. From the precursors obtained by this method, the BSCCO superconducting phases were obtained by an appropriate thermal treatment. The formation of the superconducting phases was identified by X-ray diffraction analysis.

Keywords

Oxalate, Coprecipitation, Solubility, Superconductors

Introduction

After the report of high T_c superconducting ceramics by Bednorz and Muller [1] it followed the discovery of the systems Y-Ba-Cu-O (T_c > 90K) [2] and Bi-Sr-Ca-Cu-O (T_c  105 K) [3]. The later system is technically attractive, but its value is diminished by the difficulty of obtaining single phase materials.

Superconducting oxide materials are commonly obtained by conventional solid-state reactions from metal carbonates and oxides. Wet chemical methods (unconventional) have been increasingly used in the production of high T_c ceramic superconductors [4-7]. The oxalate coprecipitation has been frequently employed for preparing various superconducting systems such as La-(Ba,Sr)-Cu-O and Y-Ba-Cu-O [5-7]. Reports about the preparation of Bi-based superconducting compounds from oxalate precursors are sparse in literature [4, 8].

The pH values reported in the literature for the coprecipitation of these oxalates are contradictory. Some questions have been raised about the oxalate method, because of the relative solubility of the Ba, Ca, Sr and Cu oxalates. This fact creates some difficulties in controlling the compound stoichiometry. In this paper we report a systematic analytical study of the coprecipitation conditions for the oxalates used as precursors for superconducting materials in the BSCCO system.

Theoretical Considerations on the Solubility of Oxalates

Our first objective was to establish the optimal coprecipitation conditions of metal oxalates, the formulas describing the solubility of oxalate precipitates as a function of pH and oxalic acid excess.

The solubility of the salt B_mA_n of a weak acid H_mA is a function of the pH via the ionization equilibriums of the acid, described by its acidity constants K_a:

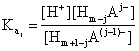, , j = 1, …, m   (1)

such as the total concentration of the different species that include A except the precipitate, is:

[A]_t = [A^m-]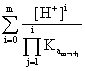                                                                                 (2)

On the other hand, species giving complexes with the cation Bⁿ⁺ will increase the solubility via the complexing equilibriums, described by the stability constants (for the sake of simplicity, charges of the species were not be given):

BL_j-1 + L  BL_j, , j = 1, …, p                                           (3)

where p is coordinating number (different from cation charge, n), or by the cumulative constants:

, i = 0, …, p                                                               (4)

The total concentration of the species that contain B, except the precipitate, if only one complexation agent (ligand) were present, will therefore be:

                        [B]_t = [Bⁿ⁺]                                                                         (5)

The solubility product of the salt B_mA_n will be given by the equation:

                        P_s = [Bⁿ⁺]^m[A^m-]ⁿ = 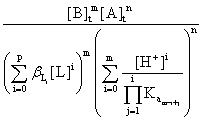                                       (6)

If the species that contain B and A result exclusively from the partial dissolution of the precipitate B_mA_n and its solubility, in the given conditions is S/(mol∙l^-1), then [B]_t = mS; [A]_t = nS and:

                        P_s = 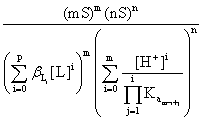                                                              (7)

The solubility is thus given by:

                        S = 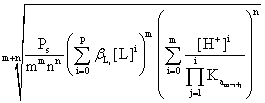                                               (8)

If there are more possible ligands (LX): L1, L2, ..., then the first sum must contain terms for all of them:

                        S = 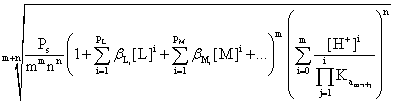               (9)

For an excess c_A of the precipitating anion A^m-, the amount resulted from the partial dissolution of the precipitate is negligible: nS  c_A+  and [A]_t  c_A; the Bⁿ⁺ concentration from the solubility product will then be:

                        [Bⁿ⁺] =                                                                                             (10)

and the total amount of B outside the precipitate, [B]_t will be given, from (5) and (2), by:

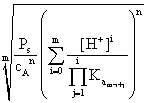
                        [B]_t =  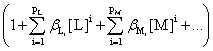                   (11)

Now, in the particular case of oxalates precipitation we must consider the two ionization constants of oxalic acid, K₁ and K₂, and in the absence of other complexing agents in the solution (like NH₃), the possible ligands are the OH^- ions, certainly present in aqueous solutions, and the C₂O₄^2- ions itself. Since the chosen pH-domain was rather acid (0 to 6), the formation of higher hydroxo-complexes can be neglected, and we considered only the [B(OH)]⁽ⁿ⁺¹⁾⁺. The OH^- concentration is given by:

[OH]^- = 10^-14[H⁺]^-1 = 10^pH-14

On the other hand, the concentration of the complexing C₂O₄^2- ions will be determined by the pH; if c₀ /(mol∙l^-1) is the excess of oxalate, the relation is:

                        [C₂O₄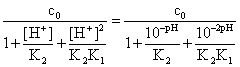^2-] =                                            (12)

The oxalate ion gives complex ions [B(C₂O₄)_j]^(n-2j)+ with many cations; it is worth noting that some cations give also neutral complexes, e.g. [CuC₂O₄], with a certain solubility. Therefore, the concentration of the metal B not included in the oxalate precipitate, i.e. present in the solution as simple Bⁿ⁺ ion, as hydroxo-complex [B(OH)]^(n-1)+ and as complex oxalates [B(C₂O₄)_j]^(n-2j)+ will be:

                        [B]_t = 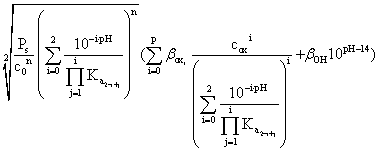               (13)

The solubility will therefore be a complicated function of the pH and the excess oxalate concentration [4,9]. A major difficulty in this field is the great dispersion of the reported values for the formation constants of the complex compounds, their solubility products, as well as the dependence of these constants on the solution ionic strength [10-13]. The selected parameters are P_s - solubility product, β_i,OH =[B(OH ^-)_i^(n-i)+]/([Bⁿ⁺][OH^-]ⁱ) – formation constants for the hydroxocomplexes, =[B(C₂O₄^2-)_i^(n-2i)+]/[Bⁿ⁺][C₂O₄^2-]ⁱ) - formation constants for the oxalate-complexes, and pK₁ = 1.23, pK₂ = 4.2 and calculated values are given in Table 1.

Table 1. Selected parameters for oxalate precipitation

Cation		Cu^2+	Ca^2+	Sr^2+	Ba^2+	Bi^3+	Y^3+	Pb^2+
-log Ps		7.54	8.64	7.25	6.9	22.3*	26.5	10.5
log βi,OH		6.7	1.5	0.8	0.9	-	8.5	6.9
log	i=1	6.23	1.66	1.25	0.6	6.10	6.5	4.91
	i=2	10.27	2.69	1.9	2.2	8.38	10.9	6.76
	i=3					8.15	11.4

* for Bi(OH)C₂O₄

An original computer program written in Basic was applied for plotting the oxalate solubility curves as a function of pH and oxalic acid excess [14,15]. A logarithmic scale was used for representing the solubility curves of various cations, which makes possible the plot of all curves on the same diagram. The total concentration of the soluble species of each metal cation as a function of pH was plotted, for different values of oxalic acid excess.

The input values are the limits of the studied pH-domain (pH_min and pH_max), the oxalate excess (mol∙l^-1), and the divisions of the pH-scale (pH units per division). The scale for the ordinate can be settled in advance (y_min, y_max). The curves can be plotted for a certain cation or, successively, for all the selected cations (Cu²⁺, Ca²⁺, Sr²⁺, Ba²⁺, Bi³⁺, Y³⁺, and Pb²⁺), on the same diagram.

Experimental

The steps of the experimental approach are given in fig. 1.

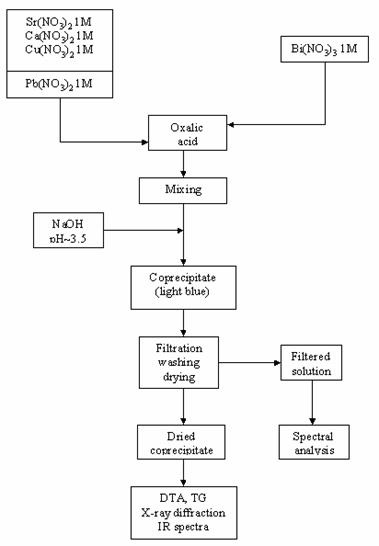
Fig. 1. Flow chart of the coprecipitation process

The coprecipitation was carried out as follows [16,17]: solutions of Sr(II), Ca(II) and Cu(II) 1M were prepared by dissolving the respective nitrate salts. In order to avoid the precipitation of basic Bi nitrate, a 1M Bi(III) solution was prepared by dissolving bismuth nitrate with nitric acid. The nominal composition was Bi:Sr:Ca:Cu = 2:2:2:3. Stock solutions of Sr, Ca and Cu nitrates were mixed. The obtained mixture and the corresponding volume of Bi nitrate were poured simultaneously into a 0.5 M solution of oxalic acid in excess, under stirring. A solution of 1 M NaOH was added under stirring to achieve a pH value of 3-3.5. The optimal pH value was determined from the theoretical solubility curves. The light blue coprecipitate was filtered, washed with water (until free of Na⁺) and dried.

The experimental determination of the coprecipitation degree of the Bi³⁺, Sr²⁺, Ca²⁺ and Cu²⁺ was performed by spectral analysis of the solution obtained after precipitates filtration. This coprecipitate was subjected to DTA, TG and X-ray powder diffraction analysis (see fig. 1).

Results and Discussion

Figures 2-5 present the calculated solubility curves for a value range of the pH from 0 to 6, and for oxalic acid excess concentrations of 0.05, 0.1, 0.2 and 1 mol∙l^-1.

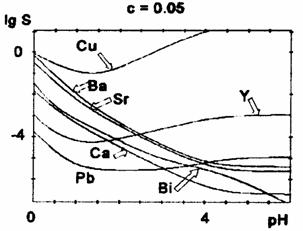
Fig. 2 Oxalate solubility curves for oxalic acid concentration c = 0.05 M

            All curves (except for Bi³⁺) present a minimum of the solubility which can be assigned to the action of two opposite factors: the protonation of oxalate ions in a strongly acidic medium and the formation of complex oxalates at higher pH-values, when the available oxalate concentration is rising.

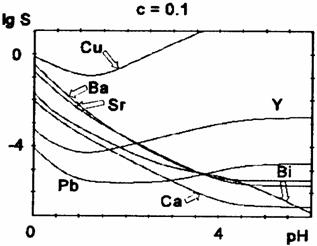
Fig. 3 Oxalate solubility curves for oxalic acid concentration c = 0.1 M

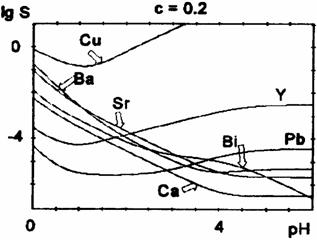
Fig. 4 Oxalate solubility curves for oxalic acid concentration c = 0.2 M

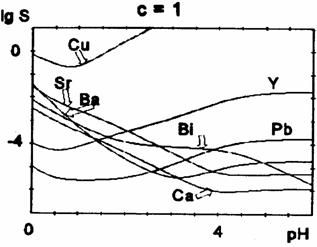
Fig. 5 Oxalate solubility curves for oxalic acid concentration c = 1 M

The position of the minimum (i.e. the optimum pH-value for the precipitation) and its depth depends also on the initial concentration of oxalic acid (table 2).

Table 2. Optimum pH-values for the oxalates precipitation

C(H2C2O4) mol∙l^-1	0.05	0.1	0.2	1.0
Cu^2+	1.2-1.6	2.1-2.3	0.8-1.3	0.7-0.8
Ca^2+	>4.9	>4.8	>4.4	4.1-4.3
Sr^2+	>5.1	>5.7	4.7-5.2	4.2-4.9
Ba^2+	>4.7	>4.5	3.7-4.5	2.8-3.3
Pb^2+	1.5-3.0	1.5-2.3	1.3-2.2	0.8-1.5
Y^3+	1.0-1.5	0.9-1.4	0.7-1.2	0.4-0.8

For higher oxalic acid concentrations, the minimum is shifted towards lower pH-values and becomes less pronounced. We notice a decrease of the solubility at lower pH-values (before the minimum) and a slight increase at the minimum and beyond it for higher oxalic acid concentrations. For Cu²⁺,Y³⁺, and Pb²⁺, there is a marked solubility increase at higher pH-values (after the minimum), because of the rather high stability of the polyoxalate complexes, while for Ca²⁺, Sr²⁺, Ba²⁺ there is only a little rise of solubility, for high oxalate concentrations. For Bi(III) the precipitate is assumed to be Bi(OH)C₂O₄.

The most difficult is the control of copper oxalate precipitation, which displays the highest solubility, because copper ions are rapidly complexed by increasing the pH. The theoretical solubility curves show that at pH between 3 and 4, the copper oxalate is almost completely dissolved. The minimum of the solubility curves of copper, lead and yttrium oxalates are at pH between 1 and 2; for calcium, strontium and barium at pH between 4 and 5. The solubility of calcium, strontium, barium and bismuth precipitate increase at more acidic pH, right in the domain where the copper solubility reaches a minimum. Obviously, it is quite difficult to choose the optimum pH value to ensure the quantitative oxalate coprecipitation in the Bi-Ca-Sr-Cu system. The experimental results proved that at pH lower than 3, the Ca and Sr oxalates are not quantitatively precipitated. On the other hand, by the simultaneous coprecipitation of the four cations at pH about 3 - 3.5 units, the solubility of Cu oxalate is negligible (lower than for Cu oxalate separately precipitated). It can be assumed that the presence of other cations in solutions displaces the solubility equilibrium of Cu oxalate. Therefore, the optimum pH value for the quantitative precipitation of oxalates in the Bi-Sr-Ca-Cu system is about 3-3.5 units, in 0.1 M oxalic acid solution. The increase of oxalic acid concentration shifts the solubility minimum towards lower pH values. It should be mentioned that the optimal pH values reported in the literature for the coprecipitation of oxalate are contradictory. Our data may help in the selection of right condition. These diagrams can be also used to establish the oxalate coprecipitation conditions for the Y-Ba-Cu-O system.

Conclusions

The oxalate coprecipitation is an appropriate method for the synthesis of precursors for superconducting materials. There are some difficulties to control the quantitative coprecipitation in the Bi-Sr-Ca-Cu oxalate system. The oxalate solubility study shows that Cu-oxalate displays the highest solubility, because Cu²⁺ is rapidly complexed by increasing pH. The precipitation of Ca²⁺, Sr²⁺ and Ba²⁺ ions is not quantitative at the lower pH (pH < 3). The presence of other cations in solution displaces the solubility equilibrium of Cu oxalate towards lower solubility.

The optimum pH value for the quantitative oxalate coprecipitation in the Bi-Sr-Ca-Cu- system was established at 3,0 - 3,5, at the optimum oxalic acid concentration of 0,1M. Using this method, the superconducting compounds of the Bi-Sr-Ca-Cu-O type were obtained, with T_c = 85 K.

References

1. J. G. Bednorz and K. A. Miiller, Z. Physik B, 64, 1986, 198.

2. M. K. Wo, J. R. Ashburn, C. J. Torng, P. H. Hor, R. L. Meng, L. Gao, Z. J. Huang, Y. O. Wang and C. W. Chu, Phys. Rev. Lett., 58, 1987, 908.

3. H. Maeda, Y. Tanaka, M. Fukutomi and T. Asano, Jap. J. Appl. Phys. , 27, 1988, L209.

4. Y. Zhang, Z. Fang, M. Muhammed, K. V. Rao, V. Skumlyev, H. Medelius and J. L. Costa, Physica C, 157, 1989, 108.

5. D. J. Jorgensen, H. Schiittler, D. G. Hinks, D. W. Capone, K. Zhang, M. B. Brodsky and D. J. Scalapino, Phys. Rev. Lett., 58, 1987, 1027.

6. Z. Wang, M. Henry, J. Livage and LRosenman, Solid State Commun., 64, 1987, 881.

7. F. G. Karioris and E. R. Vance, Mat. Letters, 6, 1987, 16.

8. G. Marbach, S. Stotz, M. Klee and J. W. C. De Vries, Physica C, 161, 1989, 111.

9. F. Caillaud, A. Smith and J. F. Baumard, L'Industrie Ceramique, 835, 1989, 118.

10. ***, Stability Constants of Metal Ion Complexes, Suppl. l, Special Publ. no. 25, Chem. Soc., London, 1970.

11. G. Martell and RM. Smith, Critical Stability Constants of Metal Ion Complexes, Part B, Organic Ligands, Pergamon Press, 1977.

12. Y. Lurie, Handbook of Analytical Chemistry, Moscow, 1975.

13. IUPAC Chemical Data, Series 22, Stability Constants of Metal Ion Complexes", Part B, Organic Ligands, Pergamon Press, 1979.

14. L. Marta, O. Horovitz, M. Zaharescu, Proceedings “Key Engineering Materials” of 5^th Conference of the European Ceramic Society, Versailles, 132-136, 1997, 1239.

15. Marta, O.  Horovitz, L.  Kekedy and I. Haiduc, Proceedings of National Conference on Chemistry and Chemical Engineering, Bucharest, 1, 1993, 291.

16. L. Marta, M. Zaharescu, L. Ciontea and T. Petrisor, Appl. Supercond., 11, 993, 677.

17. L. Marta, M. Zaharescu, T. Petrisor, D. Crisan, L. Ciontea and I. Haiduc, 3^rd Euro-Ceramics Conference Proceedings, 2, 1993, 623.