MDF – A New QSPR/QSAR Molecular Descriptors Family
Lorentz JÄNTSCHI
Technical University of Cluj-Napoca, Romania
Abstract
Motivation
In the present are many QSAR/QSPR models, based on varied considerations, from mathematical through topological and geometrical to 3D molecular geometry approaches.
Idea
The idea is to create a unitary approach, based on a minimal set of well-known truths, capable to generate an efficient model of property behavior depending on molecular structure.
Method
First step in order to reach the proposed goal is to create a huge family of molecular descriptors starting from molecular structure as a graph, considering the bonds and bond types, atom types and a most probable 3D geometry of the molecule. More, using this family of molecular descriptors, a preliminary selection is done in simple linear regression with the measured property. The resulted set of valid descriptors serves for multivariate regressions in order to reach the best QSAR/QSPR model.
Results
The comparisons of the obtained results with other models shows that the proposed model of Molecular Descriptors Family is superior to most of the all other models.
Advantages
The model is dependent only of the microscopic molecular structure and it can be applies at any macroscopic molecular property.
For a given molecular structure or set of structures, is necessary only one calculation of the descriptors, and can be applies to more than one measured property without changes. In other words, the MDF of a molecular structure is a molecular invariant.
Disadvantages
Because the set of molecular descriptors are huge (787968 computed values), the processing time of the model finding is time consuming.
Conclusion
Considering the obtained results, advantages and disadvantages and also the trend of computing performances, the MDF method promise a great expansion of using.
Keywords
QSAR model, Molecular descriptors, Molecular Descriptors Family
Introduction
In the last period, the structural indices for QSPR/QSAR (quantitative structure-property/activity relationship) are more frequently computed from steric (geometrical) and/or electrostatically (partial charges) regards [[1], [2], [3]] opposing to classical topological regards [[4]].
Are preferred the semi-empirical and quantum calculations with software as: Hondo95, Gaussian94, Gamess, Icon08, Tx90, Polyrate, Unichem/Dgauss, Allinger’s MM3, Mopac93, Mozyme, HyperChem [[5]].
Property/structural index regression analysis uses the classical methods of linear, multiple linear, nonlinear regression, or the expert systems or neural networks for large databases [[6], [7]].
As preliminary of analysis, some authors align the set of molecules [[8]]. More, the CoMFA method [[9]] introduces a six steps algorithm for QSAR/QSPR analysis [[10]]:
1. construct the molecules set with known activity and generate the 3D structure of molecules (eventually with one of following software’s: Mopac, Sybyl [[11],[12]], HyperChem [[13], [14]], Alchemy2000 [11], MolConn [[15]]);
2. chouse a overlapping method (overlapping of fragments choused from molecules [11, [16], [17]] or overlapping of pharmacophore groups [[18]]) and overlap virtually the spatial coordinates;
3. construct a grid which surround the overlapped molecules at (2) in standard form [9] or modified form (curvy [[19]]) and chouse a probe atom for interaction with the points of grid [[20], [21]];
4. use a empirical method (Hint [[22]]), a specific model (pharmacophore overlapping [[23]]), the classical potential energy (Lennard-Jones, Coulomb [9]), the hydrogen bonds energy [[24]], molecular orbital generated fields [[25], [26]] or any other model user defined [20] and calculate the interact values of grid induced field (3) by choused interaction field with the probe atom (3) placed into the grid points;
5. use the calculated values of interaction (4) between the grid points and probe atom to make the QSAR prediction of the known activity;
6. use the obtained QSAR parameters (5) to make the estimation of activity to molecules lending oneself to same overlapping with training set (1);
CoMFA method is a good tool to predict a varied type of biological activities such as cytotoxicity [[27]], inhibition [21,25], forming properties [[28], [29]]. More, the method uses in modeling of compounds with pharmaceutical effect [18,[30]] and HIV inhibitors [[31]].
An important task in QSAR modeling is searching of active substructures into active molecules, which give most of the measured biological response [[32]].
Searching of molecular invariants is particularly useful in case studies. The WHIM (Weighted Holistic Invariant Molecular) method in that direction compute a set of statistical indices derived from steric and electrostatic properties of molecules [[33], [34], [35]]. A variant, called MS-WHIM (from Molecular Surface) serves to molecular surface analysis [[36]]. The MS-WHIM is a collection of 36 statistical indices derived from steric and electrostatic properties and is oriented to parameterization of molecular surface [[37]].
MDF Generation
The most important part of the study is Molecular Descriptors Family (called MDF) creation. To create the MDF are necessary mathematical, physical, chemical, quantum mechanic and computer science specific arguments and instruments.
Starting with molecular structure investigations, the first step is to draw the molecule. For molecular structure representation, we use the HyperChem software (Hypercube, Inc.). The software allows us to draw the molecule (including multiple bonds and heteroatom). More, the HyperChem build-in rules was used to assign standard bond lengths, bond angles, torsion angles, and stereochemistry. The using of semi-empirical Extended Hückel model feature of HyperChem software using the Single Point Approach allow us to calculate the charge distribution on atoms inside the molecule.
The set of drew molecules now have the topology (atoms, bonds, and bond types) and topography (relative atom coordinates and partial charges) defined.
The active site of a molecule is between fragments of molecule. Not all atoms from the molecule is equal responsible of biological activity of the molecule. Therefore, a fragmentation procedure is welcomes. Many known fragmentation routines can be used or simply invented, but few it generate always sets of connected atoms.
The MDF fragmentation procedure use into fragmentation criterions pairs of atoms (i, j) in order to generate always sets of connected atoms. Four fragmentation criteria were implemented: minimal fragments (contains only the atom i), maximal fragments (contains the largest set of connected atoms excluding atom j), Szeged fragments (contain the set of vertices that are closed to i then j - distance-based criterion, distance-based fragments), and Cluj fragments (molecular substructure are generated excluding one path from i to j and then are applied the distance-based criterion - path-based criterion, path-based fragments) [[38]]. Note that the first three criterions it generate always one fragment (a molecule with n atoms it has n2-n fragments), and the last criterion it generate a number of fragments equal with number of paths from i to j which is generally different and is at least equal with n2-n [[39]].
The MDF descriptors calculation procedure use both topological and geometrical distance, six atomic properties, twenty-four interaction descriptors formulas, six overlapping interaction models, four fragmentation criterions, and nineteen fragmental property selector functions. To all 131328 resulted values, six linearization operations are applied, and it result a number of 787968 MDF members for a given molecule.
MDF Symbolism
An example of descriptor name is lmmRDCg (this is one computed descriptor from a total number of 787968). It has seven ordered letters. Let us take the descriptor name as reference for the explanation of its value for a given molecule.
The 7-th letter (g in our example) tells about the distance descriptor used. It can be g or t. The g letter is for geometric distance operator (calculated using Cartesian coordinates) and t is for topological distance operator (calculated using the associated graph of the molecule).
The 6-th letter (C in our example) tells about the atomic property used. It can be one of C (Cardinality, always 1), H (number of directly bonded hydrogen’s), M (atomic relative mass), E (the atomic electronegativity), G (the group electronegativity [[40]]), Q (the partial charge, semi-empirical Extended Hückel model, Single Point approach).
The 5-th letter (D in our example) tells about the interaction descriptor (ID) used. It uses two property values (let be p1 and p2) and a distance value (let be d). It can be one of D (for ID = d), d (for ID = 1/d), O (for ID = p1), o (for ID = 1/p1), P (for ID = p1∙p2), p (for ID = 1/p1/p2), Q (for ID = √p1∙√p2), q (for 1/√p1/√p2), J (for ID = p1∙d), j (for ID = 1/p1/d), K (for ID = p1∙p2∙d), k (for ID = 1/p1/p2/d, L (for ID = √p1∙√p2∙d), l (for ID = 1/√p1/√p2/d), V (for ID = p1/d), E (for ID = p1/d/d), W (for ID = p1∙p1/d), w (for ID = p1∙p2/d), F (for ID = p1∙p1/d/d), f (for ID = p1∙p2/d/d), S (for ID = p1∙p1/d/d/d, s (for ID = p1∙p2/d/d/d), T (for ID = p1∙p1/d/d/d/d), t (for ID = p1∙p2/d/d/d/d).
The 4-th letter (R in our example) is for interaction model. Are used as entry value a given fragment of a given atom i relative to a given atom j. It has six values, for six models. The R and r models consider that the distance is far enough to treat all interaction descriptors as scalars. The R model computes the resultant of the fragment’s atoms descriptors at position of atom j. The r model computes the resultant at origin. The M and m models consider all fragmental property cumulated into the property center of the fragment. The property center coordinates are calculated by a formula similarly with well-known mass center coordinates formula. The fragmental descriptor is calculated using property center coordinates and sum of fragmental property as fragmental property. Similarly, the M model reefer the atom j and m model refer the origin. The D and d models threat the descriptors as vectors with direction identical to distance vector. The axial projections are summed to obtain the projections of fragmental descriptor. The value of fragmental descriptor is calculated from his projections. The D model reefer the j atom and d model refer the origin.
The 3-rd letter (m in our example) denotes the fragment type. Four fragmentation criteria are used (m, M, D and P). The m letter is for minimal fragments, the M letter is for maximal fragments, the D letter is for a distance-based criterion, and the P letter is for a path-based criterion.
Explanation of the second letter of the descriptor name requires a remark. Generally, by applying a fragmentation criterion on a molecule for all pairs of atoms, at least one molecular fragment is obtained. It result a varied number of fragments, depending on number of atoms and selected fragmentation criterion.
The second letter (m in our example) is the code for uses the all values of fragments descriptors for a given model type with a given descriptor type, given distance-type and given property type and using a given fragment type by varying the pair of atoms to give a single value. On this array of fragmental descriptors a set of 19 functions are applied. The functions can be grouped as follows. Conditional group contains four functions: m (smallest fragmental descriptor value from the array), M (highest value), n (smallest absolute value), and N (highest absolute value). Average group contains five functions: S (sum of descriptor values), A (average mean for valid fragments), a (average mean for all fragments), B (average mean by atom), b (average mean by bond). Geometric group contains five descriptors: P (multiplication of descriptor values), G (geometric mean for valid fragments), g (geometric mean for all fragments), F (geometric mean by atom), f (geometric mean by bond). Harmonic group contains five functions: s (harmonic sum of values), H (harmonic mean for valid fragments), h (harmonic mean for all fragments), I (harmonic mean by atom), i (harmonic mean by bond).
The first letter (l in our example) explains how the resulted descriptor value is used in correlations. Because we use linear regression, a set of linearization functions are used. The I letter is for identity function, the i letter is for inverse function 1/x, A letter for absolute function |x|, a letter is for inverse of absolute function 1/|x|, L letter is for natural logarithm of absolute value function loge(|x|), and l letter is for simple natural logarithm function loge(x).
In order to express a general formula of molecular descriptor value, let’s denote used atomic property with AP, distance operator with DO, descriptor formula with DF, interaction model with IM, fragmentation criterion with FC, array-type superposing formula of fragment descriptors values with SF and linearization descriptor with LD. The resulted expression of a molecular descriptor is given by:
LD(SF({IM(AP,DO,DF(AP,DO),f) | f Î FC(Molecule)})) (1)
Note that not all this descriptors can be computed because we use positive defined functions as logarithm or inverse.
On a test set of 10 molecules, only 324388 values are real and distinct values. More, using a significance selector to bias the values, using a significant difference value of 10-9 for mono-varied scores the MDF members are reduced to a number of 103237 significantly different molecular descriptors.
MDF Member Formula Example
Let us consider the AiPdtQt descriptor, the last descriptor computed from our set.
Let be M the molecule and m(M) to be the total number of bonds. In order to define a fragment, a path from atom i to atom j called p or p(i,j) must be defined:
p = p0p1…pk path from i to j Û p0 = i, pk = j, p1, …, pk-1 Î M, k = d(i,j,M) (2)
where d(i,j,M) is the topological distance from atom i to atom j in molecule M.
The P fragments are:
FrP(M) = {f(i,j,p) | i, j Î M, i ≠ j}, f(i,j,p) = {a Î M\p, d(a,i,M\p) < d(a,j,M\p)} (3)
where f(i,j,p) is a P fragment of atom i relative to atom j from molecule M, p a path from i to j, a the resulted structure after the p path elimination from molecule M, and d(a,i,M\p) and d(a,j,M\p) are topological distances in M\p structure.
Note that always i Î f(i,j,p), j Î f(j,i,p), i Ï f(j,i,p) and j Ï f(i,j,p), which means that always a P fragment contain at least one atom.
A P fragmental descriptor value using f(i,j,p) fragment, d interaction model (IM), topological distance t (dt metric), partial charge Q (Q(v) partial charge of atom v) and strong nuclear force t (p1p2/d4 formula) is:
d(Q,dt,
p1p2/d4,f) = ![]() (4)
(4)
By applying the harmonic mean by bond i for all P fragments of M it result a molecular descriptor MD:
i({d(Q,dt,
p1p2/d4,f), f Î P(M)}} =  ∙m(M) (5)
∙m(M) (5)
The last step, applying of absolute (modulus) operator gives us the AiPdtQt descriptor:
AiPdtQt =
| |∙m(M) (6)
|∙m(M) (6)
MDF Database
Storing of MDF values are a database oriented system. The `MDF` database has one management part, which contain two tables: `ready` and `qsar` and more set parts (see figure 1).
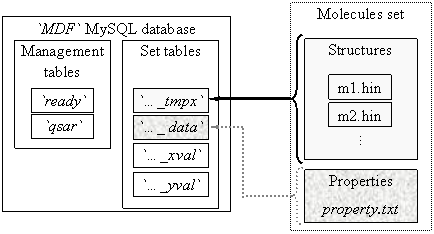
Fig. 1. `MDF` database structure
One set part contains four tables, called automatically by management programs starting with set name, and ending with one of _data, _tmpx, _xval and _yval terminations. The `ready` table tells to any client program which connect to database and want to find a QSAR model which sets of molecules are ready (complete prepared) for QSAR findings. On `ready` table the client grant is only select. The `qsar` table allows select and insert grants from clients and stores the best found QSAR models for all molecules sets from `MDF` database.
A _tmpx set table has as columns the molecules names and as rows the MDF un-linearized members (131328). A _data set table contains the measured activity for the molecules set. A _xval set table has same column names as _tmpx set table and contains at the end of preparation procedure all valid and distinct MDF members. A _yval set table has same row keys as _xval set table and contains statistical parameters of _xval corresponding row (and MDF member) relative to measured data (from _data set table): average of member values, average of member squared values, convolution product, and squared correlation coefficient. Also, a `_yval` table has a column for MDF member’s names.
MDF Generation
It is almost impossible to compute the MDF without efficient computer programs. A set of six programs completes the MDF generation task. The programs uses create table, insert, drop, delete, and select grants on `MDF` database. All programs expect running from a directory with same name as set name.
First program, a_mdf_prepare.php expects to find a subdirectory (of current directory) called hin which must contain the molecules as *.hin files ordered in same order as measured property from property.txt file from data subdirectory. The program uses property.txt file to create the _data set table and *.hin file names to create the structure of _tmpx set table.
Second program, b_mdf_generate.php is a time consuming one, and for all molecules from hin subdirectory computes and stores the MDF values into _tmpx set table. The program allows restarting and the user can delete already prepared files from hin subdirectory.
Third program, c_mdf_linearize.php generates the linearized MDF members and statistical parameters and stores it into _xval and _yval respectively set tables.
Fourth program, d_mdf_bias.php deletes all MDF members with infinite or undefined values in the first phase, and uses a sorting by squared correlation coefficient to delete again in the second phase all records with repeated value of squared correlation coefficient.
Fifth program, e_mdf_order.php recreates _xval and _yval tables by rearrangement of MDF members by squared correlation coefficient values. Finally, writes in the `ready` table a record with set name.
Now a client program can connect to the database, fetch the measured data from _data set table, MDF members values from _xval set table and preprepared statistical parameters from _yval set table and proceed to QSAR/QSPR findings. The QSAR/QSPR model finding is a multitasking one. A MySQL database server store and manage the `MDF` database. Because the findings are very consuming of time (about 5∙109 pairs of MDF members in bi-varied model) the client programs use statically memory allocation management and for multi-varied models (more than two) use heuristic algorithms for QSAR/QSPR findings. Until now seventeen heuristic programs serves us to find QSAR/QSPR models with more than two linearized descriptors.
The i_mdf_query.php program produces complete statistical analysis of QSAR/QSPR models with MDF members for all found QSAR/QSPR models from `qsar` table.
The QSPR Study
A previous studied set of 10 organophosphorus herbicides was taken [[41]] and a MDF model was build. The Y values it represent ICHR measurements. The reported r2 results in [41] for the selected compounds are r2 = 0.881 with a mono-varied regression and r2 = 0.904 with a bi-varied regression.
Table 1. Retention Chromatographic Index ICHR of 10 Organophosphorus Herbicides
|
No. |
Compound |
ICHR |
|
No. |
Compound |
ICHR |
|
1 |
3,5-diclorbenzoic acid |
7.4 |
|
6 |
2,4-D |
11.8 |
|
2 |
Dicamba |
9.8 |
|
7 |
Pentachlorophenol |
12.4 |
|
3 |
Mecoprop |
10.3 |
|
8 |
2,4,5-T |
14.3 |
|
4 |
Dichloroprop |
11.0 |
|
9 |
2,4-DB |
14.6 |
|
5 |
MCPA |
11.5 |
|
10 |
Bentazon |
18.5 |
Our best performance models use also two MDF descriptors. The computed values of descriptors are in table 2:
Table 2. Five Selected Descriptors from MDF and their Calculated Values
|
No |
Compound |
IBPdqHg (·100) |
lSDmwMt (·100) |
iHPDEQg (·100) |
lHMrtCt (·10-1) |
iBPmTEt (·10-3) |
|
1 |
3,5-diclorbenzoic acid |
34.971 |
10.794 |
15.481 |
-19.841 |
27.726 |
|
2 |
Dicamba |
42.017 |
11.192 |
16.383 |
-20.381 |
25.447 |
|
3 |
Mecoprop |
44.858 |
11.059 |
37.580 |
-27.607 |
30.227 |
|
4 |
Dichloroprop |
48.129 |
11.267 |
25.150 |
-27.607 |
29.776 |
|
5 |
MCPA |
43.772 |
10.882 |
78.065 |
-28.171 |
29.578 |
|
6 |
2,4-D |
47.760 |
11.102 |
56.324 |
-28.171 |
29.117 |
|
7 |
Pentachlorophenol |
45.248 |
11.592 |
15.550 |
-16.985 |
20.636 |
|
8 |
2,4,5-T |
56.613 |
11.462 |
60.341 |
-28.269 |
26.646 |
|
9 |
2,4-DB |
58.366 |
11.327 |
83.571 |
-34.910 |
31.084 |
|
10 |
Bentazon |
67.346 |
11.443 |
134.46 |
-21.502 |
17.443 |
The IBPdqHg MDF family member produce the best mono-varied correlation with property data. The QSPR model with this descriptor is:
ICHR = a0 + a1∙IBPdqHg (7)
where a0 = -3.371(t = -2.44, p = 4 %) and a1 = 0.318 (t = 11.44, p = 3∙10-4 %) with following global statistical results:
r = 0.971; r2 = 0.942; r2adj = 0.935; F = 131, p = 3∙10-4 %. (8)
The lHMrtCt and iBPmTEt MDF family members produce one of the best bi-varied correlation with property data. The QSPR model of them is:
ICHR = a0 + a1∙lHMrtCt +a2∙iBPmTEt (9)
where a0 = -20.46 (t = 84, p = 9∙10-11 %), a1 = -6.96 (t = -65, p = 5∙10-9 %) and a2 = -969 (t = -75, p = 2∙10-9 %) with following global statistical results:
r = 0.999; r2 = 0.999; r2adj = 0.998; F = 2924, p = 6∙10-9 %. (10)
The lSDmwMt and iHPDEQg MDF family members produce the best bi-varied correlation with property data. The QSPR model of them is:
ICHR = a0 + a1∙lSDmwMt+a2∙iHPDEQg (11)
where a0 = -62.361 (t = -43, p = 9.6∙10-8 %), a1 = 6.37 (t = 49, p = 4∙10-8 %) and a2 = 0.0587 (t = 68, p = 4∙10-9 %) with following global statistical results:
r = 0.999; r2 = 0.999; r2adj = 0.999; F = 4368, p = 1.5∙10-9 %. (12)
A leave one out cross validation procedure was applied for these three QSPR models. Following results was obtained:
r2cv-loo(ICHR, IBPdqHg) = 0.915;
r2cv-loo(ICHR, (lHMrtCt, iBPmTEt)) = 0.998; (13)
r2cv-loo(ICHR, (lSDmwMt, iHPDEQg)) = 0.999;
The correlations between descriptors of the bi-varied models are expressed by:
r2(lHMrtCt, iBPmTEt) = 0.524;
r2(lSDmwMt, iHPDEQg) = 0.043; (14)
Graphical plots of (7), (9) and (11) QSPR models are in figure 2:



Fig. 2 Plots of Best Three QSPR Models of Retention Chromatographic Index
for 10 Organophosphorus Herbicides with MDF members
Discussions
The QSPR model of IBPdqHg MDF family member give us a probability of wrong model of p = 3∙10-4 % (equation 8) and demonstrates (r2 = 0.94 reported to r2 = 0.8 from [41]) that models which consider also geometrical shape are significant better than strictly topological based models.
The QSPR models with lHMrtCt and iBPmTEt MDF family members, lSDmwMt, and iHPDEQg MDF members give probability of wrong model to p < 10-8 (equations 10 and 12).
Using of comprehensive searching into bi-varied regression (5328887466 pairs of MDF members) demonstrates that always never the best mono-varied descriptor produce also the best bi-varied regression together with another descriptor.
The cross-validation scores of models demonstrate the power of estimating properties with MDF members (r2cv > 0.91 for mono-varied models, r2cv > 0.99 for bi-varied models, equation 15).
The cross correlations from equation 14 (r2(lHMrtCt, iBPmTEt) = 0.524 and r2(lSDmwMt, iHPDEQg) = 0.043) demonstrate that is no link between using of orthogonal descriptors (Principal and/or Dominant Component Analysis) in QSAR/QSPR modeling.
The comparisons of the obtained results with other models show that the proposed methodology of model of Molecular Descriptors Family is superior to most of the all other models.
The model is dependent only of the microscopic molecular structure and it can be applies at any macroscopic molecular property.
For a given molecular structure or set of structures, is necessary only one calculation of the descriptors, and can be applied to more than one measured property without changes. In other words, the MDF of a molecular structure is a molecular invariant.
Because the set of molecular descriptors are huge (787968 computed values), the processing time of the model finding is time consuming.
Conclusions
Considering the obtained results, advantages and disadvantages and also the trend of computing performances, the MDF method promise a great expansion of using.
Using of MDF has doubtless advantages, such as better QSAR model (increasing of r2 score to 0.999 from 0.9 of compared model [41].
The MDF generation is pure based on molecular topological and geometrical considerations, do not depend on molecules environment or state. The huge number of descriptors (131328) allows successfully doing the model reduction and obtaining the best performance models.
One disadvantage of MDF can be the processing time of QSPR/QSAR model for more than bi-varied equations but is counterbalance by the performances of the obtained models.
References