Development of Model and Simulation of a Two-Phase,
Gas-Liquid Horizontal Separator
O. D. ADENIYI
Department of Chemical Engineering, Federal University of Technology, Minna, Nigeria
Abstract
In recent years, the performance requirements for petroleum process plants have become increasingly difficult to satisfy. In order to understand, design and operate the complex systems in the petroleum industries at relatively low cost and with minimum risk, mathematical modelling becomes very useful. Thus, this paper proposes some developed mathematical models for a two-phase gas-liquid horizontal separator, which is valid with an accuracy of about 1.641% based on the liquid temperature values. Simulated temperature values were 300.24 K, 299.69 K and 299.14 K with the corresponding industrial values as 300.22 K, 299.67 K and 299.11 K respectively. Within the boundaries of the limitations stated, the model could be used to predict the operation of the separator at different operating conditions, to optimize the separator products and as a tool for further expansion amongst other uses.
Keywords
Gas-liquid, two phase horizontal separator, process control, model, simulation
Introduction
Crude petroleum oil as found in nature, require pre-treatment to improve the product quality and meet current quantity and specification demanded for transportation fuels and related products. These pre-treatment processes include degassing, dewatering and desalting. Incidentally, these pre-treatment processes are also complex and require sophisticated equipment and instrumentation. As a result, the petroleum producing industries are capital intensive (Meyer, 1992). In order to understand, design and operate these complex systems at relatively low cost and with minimum risk, mathematical modelling becomes very useful. Again, the cost and risk involved in testing real life engineering systems are usually prohibitive. Thus, the preferred alternative is to develop mathematical model of the system and use same for investigating its performance.
Modelling of a chemical engineering system such as a crude petroleum separating unity involves the use of fundamental physical and chemical laws (such as the laws of conservation of mass, energy and momentum) in their general form with time derivatives included to formulate the basic equations. Assumptions, which impose limitations on the model, are also made so that the model would not be too complex and impractical. The solution of the model equations may be carried out analytically or by using computerized numerical programmes. The latter is referred to as computer simulation (Imeh, 2003; Sinnot, 2001; Stephanopoulous, 1995; Luyben, 1990).
This paper describes the development of mathematical models for gas-liquid separation process and to apply the model in simulating the operation of a gas-liquid separation unit (a horizontal two-phase separator in the continuous mode) for the separation of gas from liquid petroleum.
The following limitations were applied to the developed model:
[1] It applies to a two-phase, gas-liquid separator, [2] strictly for a crude oil/natural gas system, [3] it is based on the classification of crude oil into eleven major components, [4] its tests of accuracy is done based on the temperature of the liquid (TL) values, [5] it was generated for a system operating under normal conditions.
Description of the Gas-Liquid Horizontal Separator
A schematic diagram of the two-phase gas-liquid separator is presented in Fig 1.
The separation of a combined gas-liquid stream into separate phases can be described by the following process; the combined liquid-gas stream enters the primary separation section A (Fig. 1) which contains the inlet nozzle (which is usually tangential) or a diverter battle. This section reduces the velocity of the fluid stream and takes advantage of the initial effects of a centrifugal or an abrupt change in direction to separate the major portion of the liquid from the combined stream. The gas then moves to the secondary section B at a lower velocity. In the secondary section B, the force of gravity is used to separate entrained droplets of liquid in the gas stream. The gas moves at relatively low velocity with little turbulence. Then the gas stream moves to the coalescing section C in which the very small droplets of liquid in the gas stream are removed by impingement on a surface where they coalesce. The section utilizes a coalescer or mist extractor, which can consist of as a series of vanes, a knitted wire mesh pad or cyclonic passage. The gas stream leaves the separator with less than 0.1 gallon per million standard cubic feet, while the liquid leaves the liquid collection section D which acts as receiver for all liquid removed from the gas in the primary, secondary and coalescing sections (Richardson and Coulson, 2001; McCabe et-al, 1993).
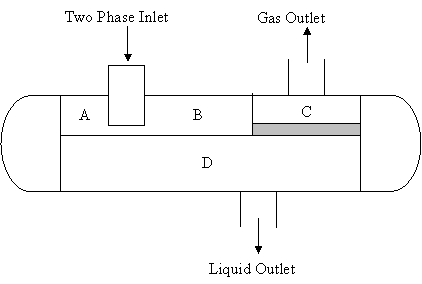
Figure 1. A two Phase gas-liquid horizontal separator
The mechanism of operation of the two-phase horizontal separator is the flash separation, where crude oil enters the separator and additional light hydrocarbon vapour are flashed. Water is separated from the crude/water mixture, the difference in densities and the tangential configuration of the stream path acts to separate the light hydrocarbon vapour and water vapour from the crude oil. Thus chemical separation (flashing) and physical separation (gravity settling, centrifugal) methods occurs simultaneously in the separator (Imeh, 2003; Perry and Green, 1997; Smith et-al, 1996).
Development of Models for the Separator
In the development of the models for the two phase gas-liquid separator, the following assumptions were made: [1] The liquid particles are spherical in size, [2] the dynamics of the vapour phase is ignored because vapour is assumed to always be in equilibrium with the liquid, [3] the mode of settlement of the liquid particles from the gas phase is free settling i.e. the settling of individual particles is not hindered by others, [4] the pressure of the liquid and vapour in the separator are not equal, [5] the liquid density, r, remain constant, i.e the temperature variations are small enough that the temperature dependence of r can be neglected, [6] heat losses are negligible and no temperature gradients exist within the separator. Therefore, the exit temperature is equal to the temperature of the liquid in the tank, [7] variables within the separator do not vary with the length of the separator.
Applying the basic principle of conservation for the separator system under study where the total mass and energy cannot be generated neither do they disappear, so that the mass balance gives (Smith et-al, 1996; Luyben, 1990):
dM/dt = SriFi - SrjFj (1)
where ri, rj are the densities of inlet and outlet streams; Fi,Fj are the volumetric flow rates of inlet and outlet streams. In terms of the total mass flow rate equation (1) becomes:
dM/dt = Wi – Wj (2)
Wi = Wo (3)
Wj = Wv + WL (4)
where Wi, Wj are the total rate of inlet and outlet streams; Wv, WL are the mass flow rates of vapour and liquid outlet streams; Wo is the mass flow rate of mixture in inlet stream. By assumption, neglecting the dynamics of the vapour phase we have:
d(rLAht) / dt = Wo – Wv – WL (5)
where rL is the density of liquid stream; ht the height of liquid in separator; A is the area of separator. Since rL and A do not varies with time, we obtain:
rLAd(ht)/dt = Wo – Wv – WL (6)
d(ht)/dt = 1/rLA[Wo – Wv – WL] (7)
Equation (7) gives the first required model. Now the total energy balance is given by (Imeh, 2003; Luyben, 1990):
dE/dt = d(U+K+P)/dt = SriFihi - SrjFjhj (8)
where E is the total energy content; U is the internal energy; K is the kinetic energy; P is the potential energy; hi, hj are the enthalpies of inlet and outlet streams. Since for liquid system the change in kinetic and potential energies are negligible, that is:
dK/dt=dP/dt = 0 (9)
dU/dt » dH/dt (10)
where H is the total enthalpy of the liquid. Neglecting the vapour phase energy dynamics:
dH/dt = Woho – Wvhv – WLh (11)
where h, hv, ho are the specific enthalpies of the liquid, vapour and mixture streams respectively. Recall that (Smith et-al, 1996; Luyben, 1990):
H = rLAhtCpL (TL – Tref) (12)
ho = Cpo(To – Tref) (13)
hv = Cpv(Tv – Tref ) (14)
h = CpL ( TL – Tref ) (15)
where Cpo,Cpv,CpL are the specific heat capacities of mixture, vapour and liquid; To,Tv,TL are the operating temperatures of then mixture, vapour and liquid; Tref is the reference temperature where the specific enthalpy is assumed to be zero. Substituting equations (12) to (15) into (11):
d(rLAhtCpLTL)/dt = WoCpoTo – WvCpvTv – WLCpLTL (16)
rLACpLd(htTL)/dt = WoCpoTo – WvCpvTv – WLCpLTL (17)
d(htTL)/dt = 1/rLACpL{WoCpoTo – WvCpvTv – WLCpLTL} (18)
Applying the product rule in differentiation (Stroud, 1995a,b; Holman, 1989):
d(htTL)/dt = TL d(ht)/dt + ht d(TL)/dt (19)
Substituting equation (7) into (19):
![]() (20)
(20)
Equating equations (18) and (20):
![]() (21)
(21)
![]() (22)
(22)
Equation (22) gives the second required model. Considering the total mass balance (Imeh, 2003; Luyben, 1996):
dMi / dt = (Woxoi / Moav) – (Wyyi / Mvav) – (Wyxi / MLav) (23)
![]() (24)
(24)
where xoi, xi, yi are the mole fractions of the component i in the mixture, liquid and vapour streams respectively. Moav, MLav,Mvav are the average molar masses of component i in the mixture, liquid and vapour streams. Since rL, A are constants equation (24) becomes:
![]() (25)
(25)
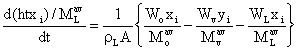 (26)
(26)
Recall from differentiation of product rules (Stroud, 1995; Holman, 1989):
![]() (27)
(27)
Substituting equation (7) into (27):
![]() (28)
(28)
Equating equations (26) and (28) to obtain:
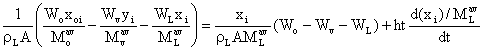 (29)
(29)
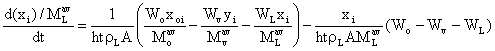 (30)
(30)
Equations (7), (22) and (30) are the developed models for the separator. In order to ensure that the degree of freedom is zero some algebraic equations were also applied (Smith et-al, 1996; Ludwig, 1994):
![]() = SyiMoi
(31)
= SyiMoi
(31)
yi = {xoiki}/{1+v(ki -1)} (32)
Syi =1 (33)
xi = yi/ki (34)
![]() = SxiMoi
(35)
= SxiMoi
(35)
ki =![]() / P (36)
/ P (36)
WL = WLZ + Kc1(hts – ht) (37)
Wv = WvZ + Kc2(Pvs – Pv) (38)
Equations (37) to (38) are the generated control equations, where WL, Wv are the outlet flow rate of liquid and vapour streams; WLZ, WvZ are the flow rates of liquid and vapour when error is zero, hts, ht are the set point and measured heights of liquid. Kc1, Kc2 are the proportional gain of the controller. Pvs, Pv are the set point and measured pressure in the separator all respectively.
Results and Discussion
The industrial and simulated results are presented in Table 1-4 and the comparison of the simulated and industrial results are presented in Table 5.
Table 1. Industrial results for the separator
|
Wo (kgs-1) |
To (K) |
rL (kgm-3) |
Pv (kNm-2) |
Tv (K) |
TL (K) |
|
83.567 83.500 84.835 83.301 83.591 83.801 83.678 83.695 83.647 83.337 85.670 85.572 85.766 85.812 83.889 85.510 |
299.67 299.67 298.56 298.56 299.11 299.11 299.67 299.67 300.22 299.11 299.67 299.67 299.67 299.67 299.67 300.22 |
854.61 854.61 852.05 852.05 852.05 849.49 849.49 854.61 852.05 854.61 849.49 844.36 849.49 852.05 854.61 849.49 |
790.834 790.834 777.044 721.886 777.044 721.886 721.886 721.886 721.886 721.886 777.044 770.149 777.044 756.360 790.834 777.044 |
309.67 309.67 309.67 309.67 310.22 309.67 309.67 310.22 309.67 308.56 309.67 309.67 309.67 309.67 310.22 309.11 |
304.11 304.11 303.00 304.11 304.11 305.22 304.11 304.11 304.11 304.11 305.22 304.67 304.11 304.67 305.22 304.11 |
Table 2. Simulated results for the separator
|
V (moles) |
TL (K) |
htL (m) |
x1/ (kg -1) |
|
0.013 0.013 0.013 0.014 0.013 0.014 0.014 0.014 0.014 0.014 0.013 0.013 0.013 0.014 0.013 0.013 |
299.6889 299.6889 298.5894 298.5835 299.1390 299.1390 299.6885 299.6882 300.2394 299.1362 299.6903 299.6896 299.6905 299.6910 299.6882 300.2407 |
1.4974 1.4999 1.5942 1.4782 1.5002 1.5155 1.5059 1.5076 1.5036 1.4808 1.6581 1.6523 1.6654 1.6680 1.5219 1.6459 |
2.54 2.54 2.53 2.48 2.53 2.48 2.48 2.48 2.48 2.49 2.53 2.53 2.53 2.50 2.53 2.53 |
Table 3. Simulated results for the separator
|
x2/ (kg -1) |
x3/ (kg -1) |
x4/ (kg -1) |
x5/ (kg -1) |
x6/ (kg -1) |
|
9.36 9.36 9.27 8.52 9.21 8.52 8.52 8.46 8.52 8.64 8.52 9.22 9.26 8.74 9.30 9.32 |
1.03 1.03 1.02 1.01 1.02 1.01 1.01 1.01 1.01 1.02 1.02 1.02 1.02 1.02 1.02 1.02 |
2.17 2.17 2.16 2.16 2.17 2.16 2.16 2.16 2.16 2.16 2.17 2.17 2.17 2.16 2.17 2.17 |
9.28 9.28 9.27 9.25 9.27 9.25 9.25 9.24 9.25 9.25 9.27 9.27 9.27 9.25 9.27 9.28 |
2.25 2.25 2.25 2.25 2.25 2.25 2.24 2.24 2.24 2.25 2.25 2.25 2.25 2.25 2.25 2.25 |
Eleven different components were simulated for, using the models developed. The mole fractions of these components are; x1 is carbon dioxide; x2 is methane; x3 is ethane; x4 is propane; x5 is isobutene; x6 is normal butane; x7 is isopentane; x8 is normal pentane; x9 is normal hexane; x10 is the heavy components of crude oil and x11 is water.
Table 4: Simulated results for the separator
|
x7/ (kg -1) |
x8/ (kg -1) |
x9/ (kg -1) |
x10/ (kg -1) |
x11/ (kg -1) |
|
1.64 1.64 1.64 1.65 1.64 1.64 1.64 1.64 1.64 1.64 1.64 1.64 1.64 1.64 1.64 1.64 |
1.74 1.74 1.74 1.74 1.74 1.74 1.74 1.74 1.74 1.74 1.74 1.74 1.74 1.74 1.74 1.74 |
2.15 2.15 2.15 2.15 2.15 2.15 2.15 2.15 2.15 2.15 2.15 2.15 2.15 2.15 2.15 2.15 |
3.83 3.83 3.83 3.83 3.83 3.83 3.83 3.83 3.83 3.83 3.83 3.83 3.83 3.83 3.83 3.83 |
5.04 5.04 5.04 5.04 5.04 5.04 5.04 5.04 5.04 5.04 5.04 5.04 5.04 5.04 5.04 5.04 |
From the tables of results (Tables 1-4) presented, the variables solved for are fairly constant despite the varying values of disturbances like Wo, To etc. The moles of the chemical species (V) had values over a rangeof 0.013 to 0.015, the temperature of liquid TL, has 298.59 to 300.24 K, while the height of liquid in the separator, htL, has 1.4974 to 1.6680 m. This infer that the control laws given by the control equations were effective in keeping output variable stable (Imeh, 2003; Stephanopoulous, 1995). It is also remarkable that the values of the variables obtained are realistic and logical. Values of V obtained in the range of 0.013 to 0.015 shows that the vapour phase of the separator’s discharge is minute.
This corroborates literature findings (Odigure et-al, 2003; Odigure, 1998; Erika et-al, 1988) and further confirmed by industrial data. The values of TL obtained are equally realistic values for crude oil under the given conditions.
A good relationship was observed between the disturbance variables and the output variables. Wo is seen to be directly proportional to the height, ht (Tables 1 and 2). The highest value of Wo of 85.812 kgs-1 has a corresponding highest value of ht, as 1.6680 m and vice versa for the lowest values. To was seen to be directly proportional to TL where a high value of 300.22 K corresponds to an equally high value of TL of 300.24 K and vice versa. In the same vein, V was observed to vary directly with Pv and indirectly with Tv (Luyben, 1990; Seborg, 1989). Table 5 present the deviation calculated between the industrial and simulated, this deviation obtained was 4.996 giving a mean error value of 1.641 % based on TL values.
Table 5: Comparison of Simulated and Industrial temperatures
|
Simulated (K) |
Industrial (K) |
Absolute Deviation (K) |
Error (%) |
|
299.69 299.69 299.56 298.56 299.14 299.14 299.69 299.69 300.24 299.14 299.69 299.69 299.69 299.69 299.69 300.24 |
304.11 204.11 303.00 304.11 304.11 305.22 304.11 304.11 304.11 304.11 305.67 304.69 304.67 304.67 305.22 304.11 |
4.42 4.42 3.41 5.52 4.97 6.08 4.42 4.42 3.87 4.97 5.53 4.42 4.98 4.98 5.53 3.87 |
1.453 1.453 1.125 1.815 1.634 1.992 1.453 1.453 1.273 1.634 1.812 1.435 1.635 1.635 1.812 1.273 |
On one hand, the model proved valid because of the low percentage error generated while on the other hand, the error generated could be traced to some of the assumption made. Parameters such as the controller gain, area of separator, and steady state values could have contributed. The numerical integration method used in solving differential equations could also have introduced truncation errors in the process of iteration (Stroud, 1995).
Conclusion
Modelling is a very important tool used in the oil industries to describe operating systems. This paper proposes some developed mathematical models for a two-phase gas-liquid horizontal separator, which is valid with an accuracy of about 1.641% based on the liquid temperature values. Within the boundaries of the limitations stated, the model could be used to predict the operation of the separator at different operating conditions, to optimize the separator products and as a tool for further expansion amongst other uses.
References
Erika, V.N.; Rasina, M.G. and Rudin, M.G. (1988) “The Chemistry and Technology of Petroleum and Gas” English Ed., Mir Publication, Moscow, pp.22-59.
Holman, P. J. (1989) “Empirical methods for engineers”, 4-th edition, McGraw Hill, Singapore, pp. 76-79.
Imeh, I. E. (2003) “Mathematical modelling and Computer simulation of a two-phase, gas liquid horizontal Separator”, B.Eng. Thesis, Federal University of Technology, Minna, Nigeria, pp. 30-54.
Ludwig, E. (1994) “Applied Process Design for Chemical and Petrochemical Plant”, Gulf Publishing Company, Texas, 3-rd edition, Vol. 1, pp. 224-271.
Luyben, W.L. (1990) “Process modelling, simulation and control for chemical engineers,” 2nd edition, McGraw Hills , Singapore, pp. 15-38.
McCabe, W.L.; Smith, J.C. and Harriot P. (1993) “Unit Operations of Chemical Engineering”, McGraw Hill Inc., New York, 5-th Edition, pp. 521-522.
Meyer, R.A. (1992) “Encyclopaedia of Physical Science and Technology”, 2-nd edition, Academic Press Inc., Vol. 9, London, pp.519-528.
Odigure, J. O. (1998) “Safety, loss and pollution prevention in Chemical Industries”, Jogids and Associates, Minna, Nigeria, pp. 57-58.
Odigure, J.O., Adeniyi, O.D. and Abdulkareem, A.S. (2003) “Mathematical modeling and simulation of a Non-Ideal Continuous Stirred Tank Reactor in a Saponification Pilot Plant” A.M.S.E., Lyon, France, Vol. 64, No. 3, pp. 41-54.
Perry, R. H. and Green, D.W. (1997) “Perry’s Chemical Engineering Handbook”, McGraw Hill, New York, pp. 1-18.
Richardson, J.F. and Coulson, J.M. (2001) “Coulson and Richardson Chemical Engineering”, Butter Worth-Heinemann, Great Britain, 3-rd Ed., Vol. 2, pp. 30-42.
Seborg, D.E.; Edgar, T.F. and Mellichamp, D.A. (1989) “Process Dynamics and Control”, John Wiley and Sons Inc., USA, pp. 3, 10-11.
Sinnot, R.K. (2001) “Coulson and Richardson’s Chemical Engineering”, Butter Worth-Heinemann, Great Britain, 3-rd Ed., Vol. 6, pp. 339-462.
Smith, J.M.; Vanness, H.C. and Abott, M.M. (1996) “Introduction to Chemical Engineering Thermodynamics”, McGraw Hill Company Inc., Singapore, pp. 315-316.
Stephanopoulous, G. (1995) “Chemical process Control- An introduction to theory and practice”, 4-th edition, Prentice Hill Inc., New York, pp. 40-59.
Stroud, K. A. (1995) “Engineering Mathematics”, Macmillan Press Ltd., London, 4-th Ed., p.168.
Stroud, K. A. (1995) “Further Engineering Mathematics”, Macmillan Press Ltd., London, 4-th Ed., p.223.