Water Activated Carbon Organics Adsorption
Structure - Property Relationships
Lorentz JÄNTSCHI
Technical University of Cluj-Napoca, Romania, http://lori.academicdirect.org
Abstract
Investigation (determination) of chemical compounds properties need time and many resources when is performed by classical way, or experimentations. Nowadays a number of quantitative structure-property relationships (QSPRs) were developed in order to shorting the research and analysis time of chemical properties on classes of compounds. The ability of the molecular descriptor family (MDF) was used to produce QSPRs for estimating the adsorption onto activated carbon in water. A number of sixteen organics and theirs adsorption onto activated carbon in water serves for QSPRs obtaining. The MDF methodology include the three-dimensional model of the molecules building using the HyperChem software, MDF members generating using a set of Pre Hypertext Processor (PHP) programs, storing using a MySQL database server, and finally with a set of Delphi Multiple Linear Regression programs structure-property relationships findings. A number of 105319 MDF members enter into multiple linear regressions findings. Five from our best QSPRs are presented, one mono-varied, two bi-varied and two tri-varied models. The MDF QSPR methodology has big potential in finding QSPR models and is proved for adsorption onto activated carbon in water of studied organics.
Keywords:
Organics Adsorption, QSPR, MDF
Introduction
The adsorption experimental data enable to evaluate the adsorptions for the chemicals of interest but if the numbers of chemical are large is most useful to develop quantitative structure-property relationship (QSPR) models in order to estimate the adsorptions of new organics before synthesis. Note that studies of adsorption onto activated carbon in water were previously reported [1]-[4].
Previous reported models use molecular descriptors indices, as proposed by Randic [5], Kier and Hall [6].
Starting from the idea that molecular topology of chemicals influence theirs properties, many QSPRs were developed. Pure topological indices are represented by the Wiener [7], Szeged [8], [9], and Cluj [10], [11]. The MDF differ from them by including also the topographical parameters into the calculation.
The aim of the present paper is to use the ability of molecular descriptor family on adsorption onto activated carbon in water of sixteen compounds for finding the quantitative structure-property relationships.
Materials
The adsorption onto activated carbon in water for the sixteen organics was taken from a previous study (table 1, [12]). Table 1 contains the name of the organics, the organics planar structure and the measured adsorption.
Table 1. The set of organics and their adsorptions into carbon water activated
|
No. |
Molecule |
Planar structure |
Adsorption |
|
1 |
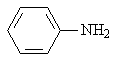
Aniline |
|
1.636 |
|
2 |
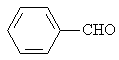
Benzaldehyde |
|
1.916 |
|
3 |
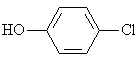
4-Clorophenol |
|
2.089 |
|
4 |
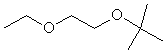
1-Etoxy-2-tertbutoxy ethane |
|
1.663 |
|
5 |
4-Nitrophenol |
|
2.242 |
|
6 |
Phenol |
|
1.702 |
|
7 |
Vanillin |
|
2.119 |
|
8 |
1-Butanol |
|
0.910 |
|
9 |
1-Pentanol |
|
1.408 |
|
10 |
2-Methyl-1-butanol |
|
1.228 |
|
11 |
1-Hexanol |
|
1.770 |
|
12 |
L-tyrosine |
|
1.795 |
|
13 |
L-phenylalanin |
|
1.787 |
|
14 |
L-tryptophan |
|
2.111 |
|
15 |
m-Cresol |
|
1.667 |
|
16 |
Benzoic Acid |
|
1.763 |
The previous reported study [12] use compounds from table 1 to obtain the predicted adsorption by use of multiple linear regression (MLR) analysis and neural networks (NN) and three molecular connectivity indices [13]. The results were:
· MLR QSPR model:
r2 = 0.665; s = 0.206; F = 27.3 (1)
where r2 is the squared of correlation coefficient, s the standard error and F Fischer parameter
· NN QSPR model:
r2 = 0.658; s = 0.208; F = 26.9 (2)
Note that the proposed models does not significantly different one from other (the squared correlation coefficient between predicted values are 0.967).
Method
First step in QSPR modeling using the molecular descriptor family was sketching up the three-dimensional structure of each compound using the HyperChem software [14], software that allows assigning standard bond lengths, bond angles, torsion angles, and stereochemistry.
Using MySQL database server and PHP programming language the molecular descriptor family database was created and gives a total number of 335657 MDF members. After filtration a total number of 105319 distinct members were included into a multiple linear regression QSPRs findings procedure. Each descriptor has a distinct name which collects the ways of his calculation. A MDF member name has seven letters with the following significances: the distance descriptor used (seventh letter), atomic property (sixth), interaction descriptor (fifth), interaction model (fourth), the fragment type (third), molecular superposing of fragmental descriptors method (second), and linearization procedure (first).
More details about MDF are in [15].
The best MDF QSPR models are recorded into the database by the client program which found the model. The MLR procedures was runs for mono-varied (simple linear regression), bi-varied and tri-varied associations of MDF members.
A client-server application provides at the end of findings a report with the statistical analysis of found QSPRs.
Results
The calculated values of MDF members from selected best QSPR models for adsorption onto water activated carbon of sixteen organics are in table 2.
Table 2. The calculated values of MDF members for Organics set
|
No |
Mono |
Bi-varied |
Three-varied |
|||||
|
M |
iSDrDQt |
IiMMWHt |
lPMDVQg |
IsPrVHg |
IiMMWHt (∙101) |
lPMDVQg (∙10-1) |
iFMdFQg (∙105) |
ibPMtQg (∙100) |
|
1 |
7.65 |
-9.29 |
-4.21 |
3.50 |
-9.29 |
-4.21 |
270 |
3.2 |
|
2 |
3.44 |
-3.62 |
-11.3 |
1.61 |
-3.62 |
-11.3 |
1000 |
11 |
|
3 |
-1.23 |
-3.51 |
-5.41 |
1.26 |
-3.51 |
-5.41 |
36 |
0.47 |
|
4 |
4.59 |
-4.50 |
-18.2 |
1.56 |
-4.50 |
-18.2 |
2.9 |
59 |
|
5 |
-7.15 |
-1.49 |
-8.04 |
0.62 |
-1.49 |
-8.04 |
0.023 |
18 |
|
6 |
7.89 |
-7.51 |
-9.09 |
3.01 |
-7.51 |
-9.09 |
10 |
330 |
|
7 |
2.01 |
-2.01 |
-8.45 |
0.77 |
-2.01 |
-8.45 |
6.6 |
19 |
|
8 |
16.8 |
-17.6 |
-4.38 |
6.80 |
-17.6 |
-4.38 |
19 |
-20 |
|
9 |
9.40 |
-11.0 |
-6.61 |
4.22 |
-11.0 |
-6.61 |
5500 |
-18 |
|
10 |
11.1 |
-13.3 |
-7.31 |
4.85 |
-13.3 |
-7.31 |
190 |
6.5 |
|
11 |
5.83 |
-7.56 |
-10.5 |
2.84 |
-7.56 |
-10.5 |
1.9∙106 |
2700 |
|
12 |
1.07 |
-1.25 |
-21.6 |
0.40 |
-1.25 |
-21.6 |
360 |
13 |
|
13 |
1.41 |
-1.56 |
-22.5 |
0.63 |
-1.56 |
-22.5 |
5700 |
19 |
|
14 |
0.80 |
-1.17 |
-13.1 |
0.42 |
-1.17 |
-13.1 |
3.1∙105 |
0.4 |
|
15 |
4.60 |
-6.81 |
-11.9 |
2.31 |
-6.81 |
-11.9 |
170 |
320 |
|
16 |
3.07 |
-2.60 |
-18.5 |
1.22 |
-2.60 |
-18.5 |
26 |
160 |
Table 3 contains the selected QSPRs obtained:
Table 3. Water activated carbon MDF QSPRs organics adsorption models
|
No |
Var |
QSPR |
|
1 |
1 |
1.99-57.99·iSDrDQt |
|
2 |
2 |
2.58+2.97∙10-3∙lPMDVQg-22.59∙IsPrVHg |
|
3 |
2 |
2.58+8.53∙10-1∙IiMMWHt+2.95∙10-3∙lPMDVQg |
|
4 |
3 |
2.57+8.62∙10-1∙IiMMWHt+2.98∙10-3∙lPMDVQg+6.01∙10-5∙ibPMtQg |
|
5 |
3 |
2.57+8.57∙10-1∙IiMMWHt+2.95∙10-3∙lPMDVQg+8.02∙10-13∙iFMdFQg |
The associated statistics with the QSPRs are in table 4 (r correlation coefficient, r2 square of correlation coefficient, s standard error, F Fisher parameter, p p-value, and r2cv leave one out cross-validation squared correlation coefficient).
Table 4. Statistics for MDF QSPRs
No |
r |
r2 |
s |
F |
p% |
r2cv |
|
Mono-varied |
||||||
|
1 |
0.927 |
0.859 |
0.134 |
86 |
2.4∙10-5 |
0.803 |
|
p-value (t Stat) Intercept: 1.16∙10-16(45.85); iSDrDQt: 2.43∙10-7(-9.25) |
||||||
|
Bi-varied |
||||||
|
0.989 |
0.978 |
0.055 |
284 |
1.89∙10-9 |
0.97 |
|
|
r2(lPMDVQg, IsPrVHg) = 0.365; r2(lPMDVQg, Ads) = 0.048; r2(IsPrVHg, Ads) = 0.195 |
||||||
|
p-value (t Stat) Intercept: 3.55∙10-16 (49.35); lPMDVQg: 2.14∙10-7 (9.85); IsPrVHg: 5.69∙10-12 (-23.23) |
||||||
|
3 |
0.99 |
0.981 |
0.051 |
337 |
6.3∙10-10 |
0.975 |
|
r2(IiMMWHt, lPMDVQg) = 0.362; r2(IiMMWHt, Ads) = 0.829; r2(lPMDVQg, Ads) = 0.048 |
||||||
|
p-value (t Stat) Intercept: 1.15∙10-16 (53.85); IiMMWH: 1.89∙10-12 (25.33); lPMDVQg: 8.46∙10-8 (10.67) |
||||||
|
Tri-varied |
||||||
|
4 |
0.997 |
0.995 |
0.027 |
799 |
4.47∙10-12 |
0.981 |
|
r2(IiMMWHt, lPMDVQg) = 0.362; r2(IiMMWHt, ibPMtQg) = 0.0067; r2(ibPMtQg, lPMDVQg) = 0.0002; r2(IiMMWHt, Ads) = 0.829; r2(lPMDVQg, Ads) = 0.048; r2(ibPMtQg, Ads) = 0.175 |
||||||
|
p-value (t Stat) Intercept: 6.21∙10-19 (100.62); IiMMWHt: 4.66∙10-15 (47.75); lPMDVQg: 1.24∙10-10 (20.2); ibPMtQg: 8.56∙10-5 (5.79) |
||||||
|
5 |
0.997 |
0.994 |
0.029 |
718 |
8.45∙10-12 |
0.991 |
|
r2(IiMMWHt, lPMDVQg) = 0.362; r2(IiMMWHt, iFMdFQg) = 0.002 r2(iFMdFQg, lPMDVQg) = 0.0006; r2(IiMMWHt, Ads) = 0.829 r2(lPMDVQg, Ads) = 0.048; r2(iFMdFQg, Ads) = 0.085 |
||||||
|
p-value (t Stat) Intercept: 1.22∙10-18 (95.12); IiMMWHt: 9.08∙10-15 (45.15); lPMDVQg: 2.59∙10-10 (18.97); iFMdFQg: 1.65∙10-4 (5.38) |
||||||
The plots of QSPRs are in figures 2-6.

Figure 2. Adsorption = 1.99-57.99∙iSDrDQt

Figure 3. Adsorption = 2.58+2.97∙10-3∙lPMDVQg-22.59∙IsPrVHg

Figure 4. Adsorption = 2.58+8.53∙10-1∙IiMMWHt+2.95∙10-3∙lPMDVQg

Figure 5. Adsorption = 2.57+8.62∙10-1∙IiMMWHt+2.98∙10-3∙lPMDVQg+6.01∙10-5∙ibPMtQg

Figure 6. Adsorption = 2.57+8.57∙10-1∙IiMMWHt+2.95∙10-3∙lPMDVQg+8.02∙10-13∙iFMdFQg
Discussions
All five presented MDF QSPRs of organics adsorption onto activated carbon in water are statistical significant giving us probabilities of wrong model less than 2.4∙10-5 %.
The mono-varied MDF QSPR is based on a member that uses the topological shape (t), and the partial charge (Q) of the molecules (iSDrDQt). Almost eighty-six percents of the variation in adsorption of organics is explainable by its linear relation with iSDrDQt. This model shows us the importance of topological shape and partial change of compounds in predicting the adsorption in mono-varied models.
First bi-varied MDF QSPR (equation 2, table 3) uses lPMDVQg and IsPrVHg members, while the second bi-varied MDF QSPR (equation 3, table 3) uses IiMMWHt and lPMDVQg members. The last letters from the members name used in both bi-varied models denote the used of topological distance on bounds (t) and the geometrical distance (g) computed using the Cartesian coordinates. The penultimate letters from the members names on both models denoted the importance of the number of directly bonded hydrogen’s (H) and respectively the partial change, semi-empirical Extended Hückel model, Single Point approach (Q). Thus, we have a model in which the adsorption can be explain by the topological distance as well as the geometrical distance and a model that explain the adsorption based on pure geometrical distance descriptors. Ninety-eight percents of the variation in adsorption of organics is explainable by its linear relation with IiMMWHt, and lPMDVQg and ninety-seven percents of the variation is explainable by the linear relation with lPMDVQg, and IsPrVHg. Looking at the square of correlation coefficients between member values used in bi-varied MDF QSPRs of adsorption onto activated carbon in water of the sixteen organics, we can say that is no link between using of orthogonal descriptors (Principal and/or Dominant Component Analysis) in QSPR modeling (r2 ≈ 0.36).
The cross validation score, with leave one out, shows that the second model (no 3, table 4) is the best bi-varied model being the best MDF QSPR in term of estimation.
First tri-varied MDF QSPR uses IiMMWHt, lPMDVQg and ibPMtQg members (equation 4, table 3) and second uses IiMMWHt, lPMDVQg and iFMdFQg members (equation 5, table 3). Both tri-varied models use one member which considers the topological distance operator (t) and two members which consider the geometrical distance (g). The penultimate letters of members names implied in the both tri-varied models shows that one member uses the number of directly bonded hydrogen’s (H) and two uses the partial change from semi-empirical Extended Hückel model, Single Point approach (Q). About ninety-nine percents of the variation in adsorption of organics is explainable by its linear relation with MDF members. The square of correlation coefficients between the used members in both tri-varied MDF QSPRs (0.362, 0.006, 0.0002; 0.362, 0.002, 0.0006) prove that is no link between using of orthogonal descriptors (Principal and/or Dominant Component Analysis) in tri-varied QSPR modeling of organics adsorption onto activated carbon in water. The best tri-varied MDF QSPR is given by the equation 5, table 3, which has the best cross validation score (over 0.99); thus, this model is the best able to estimate the adsorption.
Looking at the previously reported QSPRs of organics adsorption onto activated carbon in water (expressions (1) and (2)) we can say that our results are better even if we look at the mono-, bi- or tri-varied QSPRs. The molecular descriptors family quantitative structure-property relationships are a useful tool in estimation of organics adsorption onto activated carbon in water.
Conclusions
The molecular descriptor family methodology produces QSPRs capable to predict the adsorption of the sixteen compounds being a better method comparing with previous reported MLR and/or NN analysis. More, it enabled a discussion about the nature of the measured property (adsorption). The QSPR finding based on molecular descriptor family methodology has good resources for QSPR modeling even if it is a time consuming method.
The QSPR that has the best ability to predict and estimate the organics adsorption onto activated carbon in water is:
Adsorption = 2.57+8.57∙10-1∙IiMMWHt+2.95∙10-3∙lPMDVQg+8.02∙10-13∙iFMdFQg
Two models involving IiMMWHt, lPMDVQg, and iFMdFQg molecular descriptors, and respectively IiMMWHt, lPMDVQg, and ibPMtQg found to be most relevant, contains two members being implied in both models, which denotes the stability of the models. Adsorption onto water activated carbon of the sixteen organics is strongly dependent on the partial change atomic property and number of directly bonded hydrogen’s and its causality are from both molecular topology and molecular topography nature.
References