A New Harmonics Elimination Method Applied to a
Static VAR Compensator Using a Three Level Inverter
M. BENGHANEM, A. DRAOU
Applied Power Electronics Laboratory, Department of Electrotechnics,
University of Sciences and Technology of Oran, BP 1505 El Mnaouar (31000 Oran), ALGERIA, Tel: +213-41-422377, adraou@yahoo.com
Abstract
In this paper the use of harmonics elimination method applied to a three level inverter is shown. The method that calculates the switching angles is shown. Simulations results using PSspice program are carried out to validate the mathematical model.
Moreover, the proposed harmonics elimination method was used to control the static VAR compensator (ASVC) which uses a three level voltage source inverter.
Keywords
ASVC, PSpice, PWM, Harmonics, Three-level inverter
1. Introduction
The fast growing development of ultra rapid power switching devices and the desire to reduce the harmonics has lead to the increase in use of converters for large-scale reactive power compensation. Such an SVC is made up of two level voltage source inverter and presents a fast response time, reduced harmonic pollution. However, for very high power application and voltages these SVC's are unsuitable. Recently the multilevel pulse width modulation (PWM) [1] converter topology has drawn tremendous interest in the power industry since it can easily provide the high power required for high power applications for such uses as static VAR compensation, active power filters, and so that large motors can also be controlled by high power adjustable frequency drives [2-5].
The most popular structure proposed as a transformer less voltage source inverter is the diode clamped converter based on the neutral point clamped (NPC) converter proposed by Nabae [1]. It has the advantages that the blocking voltage of each switching device is one half of dc link voltage and the harmonics contents output voltage is far less than those of two-level inverter at the same switching frequency.
The multilevel voltage source inverters unique structure allows them to reach high voltages with low harmonics without the use of transformers or series connected synchronized switching devices, a benefit that many contributors have been trying to appropriate for high voltage, high power applications [6-9]. It is well known that for a classical inverter voltages are generated with harmonics of the order (6K 1)f, and the input current at steady state contains frequency components equal to 6K f with f: output fundamental frequency [10-11] and K=1, 2, 3, … One of the solutions applied is the use of multilevel inverter topology. Fig. 1 shows the structure of a three level inverter used as a compensator each leg of the inverter is made up of four pairs of diode - GTO's.
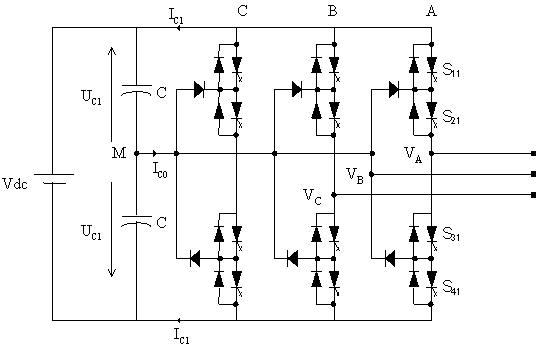
Fig.1. Topology of a three level inverter
Each represents a bi-directional switch and two auxiliary diodes allowing having zero voltage at the output of the inverter. The system obtained is connected to an RL load, the DC side is composed of two capacitors behaving as a voltage divider supplied from a DC source [13].
2. PWM control for harmonics elimination
The switching angles are either fixed by the intersection of a reference wave and a modulating signal, PWM case, or full wave control. A third alternative control method is possible when we use a system controlled by microprocessor for the switching through the pre-calculated sequences and then stored in a memory [14].
The determination of the control angles may then be carried out based on complex criteria, since the angles have already been calculated. The performances of the system depend on the choice of the criteria used for calculating the angles; it is interesting to note that any method used will consist always on eliminating the effect obtained by the presence of harmonics on the output voltage of the inverter.
Fig. 2 shows the control signals of the four switches of one leg of the three phase three level inverter and the phase voltage to the neutral point M. The pulses given in fig. 2a and fig. 2b control the switches S11 and S21. The complementary pulses to S11 and S21 respectively in fig. 2c and fig. 2d control the switches S13 and S14. The voltage between a phase and neutral point M is illustrated by fig. 2e we notice that the voltage VAM is symmetrical with respect to M. Fourier coefficients for such a signal VAM are given by:
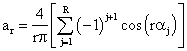 (1)
(1)
with R the harmonics range (1,2…R).
These equations are non linear, and multiple solutions are possible. But all the solutions of equation (1) must satisfy the following constraint:
![]() (2)
(2)
The non-linear equations to eliminate R-1 harmonics non multiple of three such as 5,7,11, etc. are written as follows:
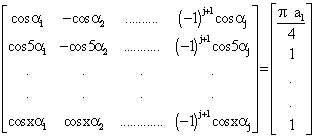 (3)
(3)
with x = 3R-1 for R even, and x = 3R-2 for R odd.
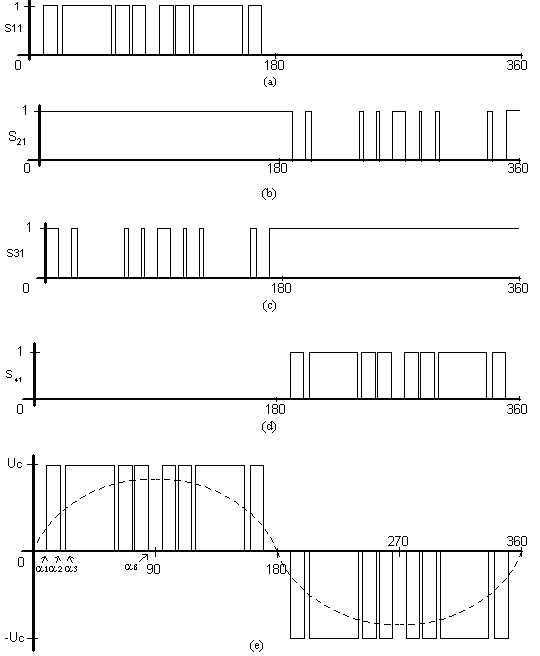
Fig. 2. Voltage between and point M VAM and the pulses for one leg of the inverter for (R=8)
(a) pulses for S11; (b) pulses for S21; (c) pulses for S31; (d) pulses for S41; (e)Voltage VAM
To solve the system of equation (3) we use Newton Raphson method, using a program MATLAB program [2]. Fig. 3 shows the trajectory of the solutions for various values of R, with modulation index "MI" varying in the interval [0 1.1].
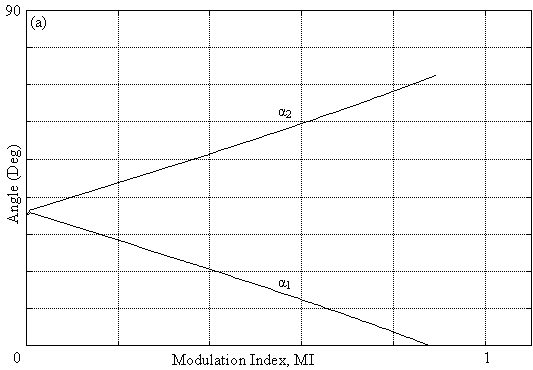
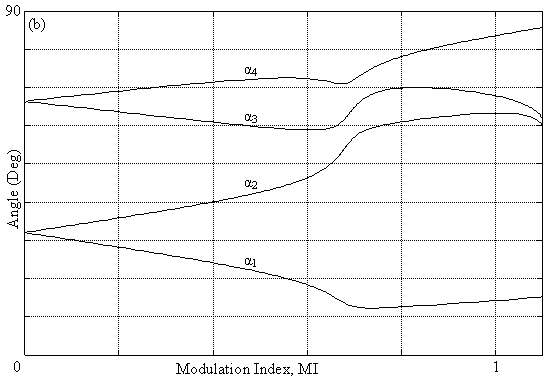
Fig. 3. Trajectories of Solutions for programmed PWM: (a) R = 2, and (b) R = 4
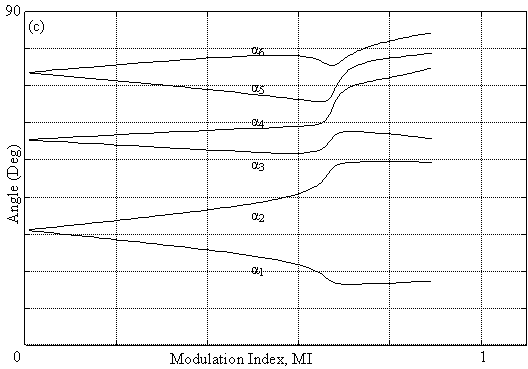

Fig. 3. Trajectories of Solutions for programmed PWM: (c) R = 6, and (d) R=8
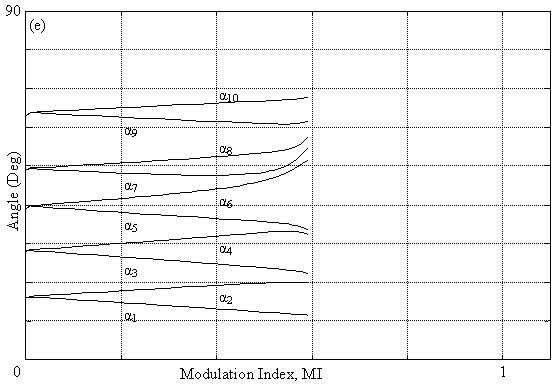
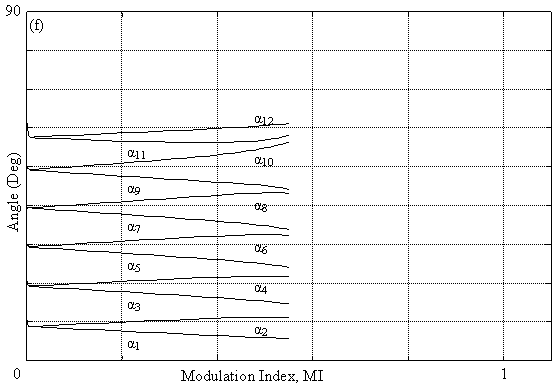
Fig. 3. Trajectories of Solutions for programmed PWM: (e) R = 10, and (f) R = 12
Fig. 3a shows that there is a linear progression of angles α1 and α2 following a negative or positive slope respectively in the interval 0 < MI < 0.6.
This note is also valid for fig. 3b, fig. 3c, and fig. 3d; however in the interval 0.6 < MI < 1.1 these trajectory become non linear, thus a more refinement of the algorithm is carried out to obtain the solutions in this interval. As for fig. 3e and fig. 3f, the system has no solutions beyond MI > 0.6. We conclude from fig. 3 that maximum of the modulation index diminish with the increase of the harmonics number eliminated illustrated. For some values of R, the trajectories of the angles get nearer which implies a decrease in the width of pulses [3].
3. Simulation results using PSpice
In order to check the validity of the calculated results of the angles, the three-phase inverter system connected to a load is modelled using PSpice.
The modelling of the switch is a simple version. It consists of an infinite value of a resistance for the open state and a low value resistance for the close state. Fig.4 represents this principle.
In order to model the inverter system by PSpice, fig. 1 schematic is used with resistive load.
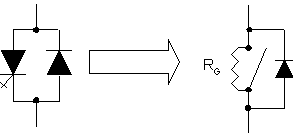
Fig. 4. Simplified model of the switch with its anti-parallel diode by PSpice
On the basis of the Pspice program various simulations have been undertaken. Fig.5 illustrates the results for the case: R = 2 and MI = 0.8, fig. 5a represents the line voltage and fig. 5b its harmonics spectra.
We notice the total elimination of harmonic of order 5.
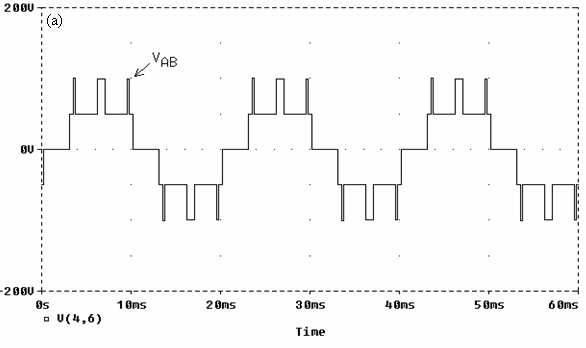
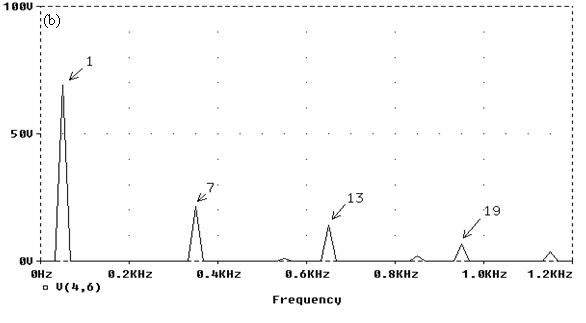
Fig. 5. Simulation results for MI = 0.8 and R = 2
(a) Line voltage, (b) Harmonics spectra; THD =31.36%
4. Application harmonics elimination method
We used the harmonics elimination method described bellow to control the static VAR compensator (ASVC) which uses a three level converter of voltage source type as shown in fig. 6. The operating principles of the system can be explained by considering the per-phase fundamental equivalent circuit of the ASVC system as shown in fig. 7.
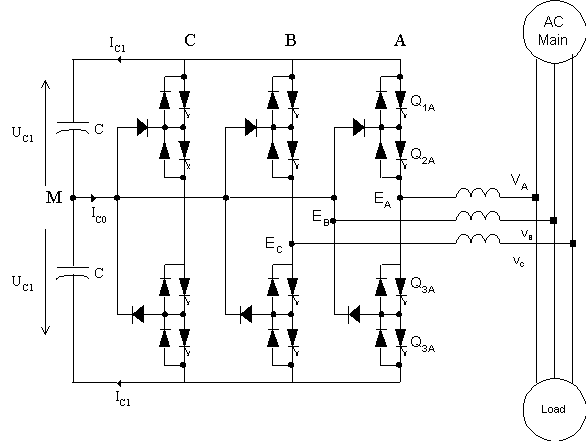
Fig. 6. Power Circuit of the ASVC
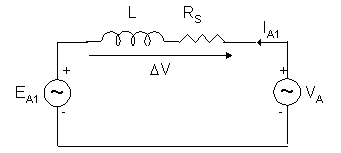
Fig. 7. Per-phase fundamental equivalent circuit
In this figure, EA1 is the ac mains voltage source. IA1 and VA are the fundamental components of the output current and voltage of the inverter supply respectively.
The ASVC is connected to the ac mains through a reactor Ls and a resistor R representing the total loss in the inverter.
Reactive power control method
As shown in fig. 8, by controlling the phase angle 'α' of the inverter output voltage, the DC capacitor voltage UC can be changed. Thus, the amplitude of the fundamental component EA1 can by controlled. In order to synthesize the control strategy of the system, the analysis is carried out using (dq) axis [3]. To achieve fast dynamic response it is required that by controlling the phase angle changes the capacitors Uc1 and Uc2 'α' will change. Small signal equivalent model system is used to calculate the transfer function of the system. The ASVC control scheme is illustrated in the block diagram of fig. 9. The design of the PI controller is described in [14].
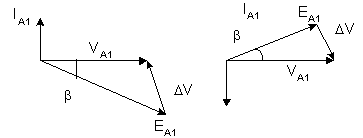
Fig. 8. Phasor Diagram for leading and lagging mode
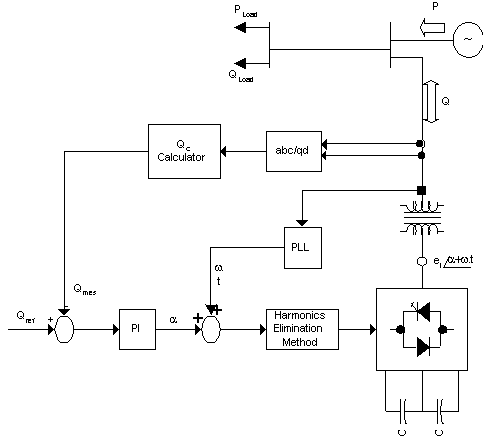
Fig. 9. Main circuit and control block diagram
Simulation results
To check the validity of the model described above a set of simulation tests have been carried out to analyse the system under steady state and transient conditions. Computer simulation is carried out using the system parameters given by: f = 60 [Hz], W = 2pf, Vs = 550 [V], Rs = 0.4 [W], L = 10 [mH], C = 1000 [mF], MI (modulation index) = 1, and R = 4, α1 = 15°, α2 = 64°, α3 = 78°, α4 = 84°.
Based on the linear model described in [13] and using root locus technique the parameters of the controller are found to be:
Kp = 10-5, Ki = 1.8∙10-4.
The amplitude of the reference was adjusted to cause the system to swing from lagging mode to leading mode. Fig. 10 shows the simulated current and voltage waveforms to step reference of reactive power.
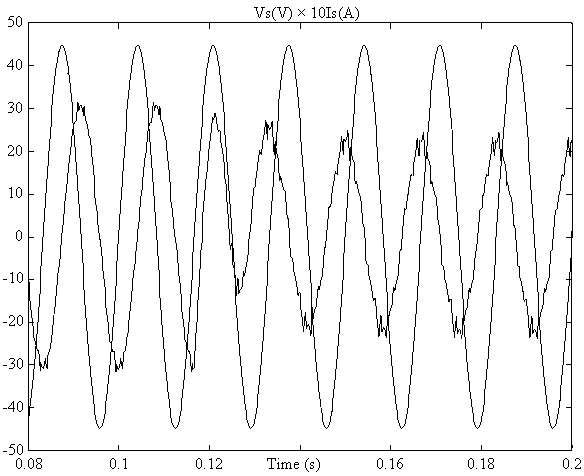
Fig. 10. Simulated current and voltage waveforms
Fig. 11 represents the current in lagging and leading mode and ther harmonics spectra respectively. We notice an increase of the amplitude of harmonics in leading mode with respect to lagging mode. This effect is caused by the DC capacitors voltage fluctuation.
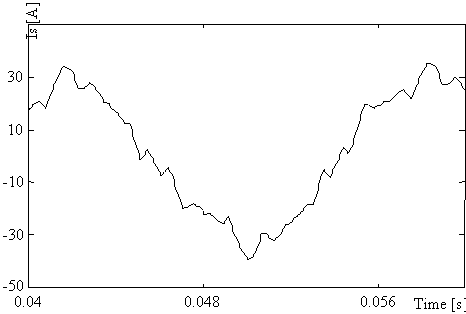
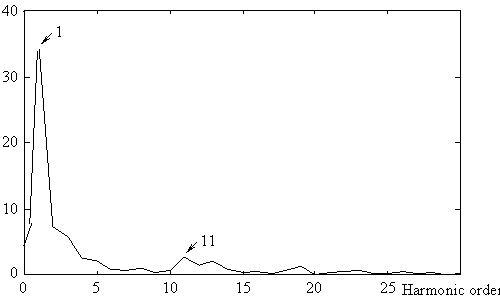
Inductive current, Harmonic spectra THD = 5.25 %
Fig. 11. Currents and harmonic spectrum (a) leading mode
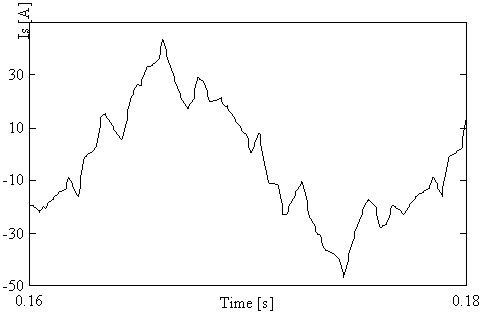
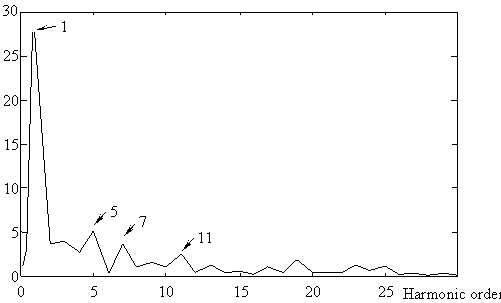
Capacitive current, Harmonic spectra THD =12.40%
Fig. 11. Currents and harmonic spectrum (b) lagging mode
Conclusions
The main conclusion results are summarised below:
· The resolution of the non-linear equations in the case of three level inverter must be carried out with a refinement of the calculation step beyond MI>0.6 so to obtain a finite solution;
· The increase in the harmonics number eliminated has a negative effect on the modulation index since with the increase of R a decrease in MI maximum follows;
· The trajectories getting nearer for MI > 0.6 implies the decrease of the switching pulses of the GTO's which itself allows for the increase in commutation losses;
The use of a three level inverter for the ASVC allows an increase of power use and voltage waveforms quality, certainly but we note that:
· The behaviour of the system depends on the operating mode;
· The DC voltage fluctuations cause apparition of eliminated harmonics.
References
1. Nabae A., Takahashi I., Akagi H., A New Neutral Point Clamped PWM Inverter’, IEEE Trans. On IA., 1981, IA-17(5), p. 509-517.
2. Akagi H., Kanazawa Y., Nabae A., Instantaneous Reactive Power Compensators Comprising Switching Devices Without Energy Storage Components, IEEE Trans On Ind. Appl., 1984, Vol. IA-20, No. 3.
3. Enjeti P.N., Lindsay J.F., Solving Nonlinear Equations of Harmonic Elimination PWM in Power Control, IEEE Trans. Ind. Appl. Electronics Letters, 1987, Vol. 32, No. 12, 4th June.
4. Moran L., Ziogas P.D., Joos G., Analysis and design of a Synchronous Solid-state Var Compensator, IEEE Trans. on Ind. Appl., 1989, Vol. IA-25, No. 4, p. 598-608.
5. Enjeti P.N., Ziogas P.D., Lindsay J.F., Programmed PWM Techniques to Eliminate Harmonics: A Critical Evaluaton, IEEE Trans. Ind. Appl., 1990, Vol. 26, No. 2.
6. Joos G., Moran L., Ziogas P.D., Performance Analysis of a PWM Inverter VAR Compensator, IEEE Trans. on Power Electronics, 1991, Vol. 6, No. 3, p. 380-391.
7. Enjiti P.N., Jakkli R., Optimal Power Control Strategies for Neutral Point Clamped (NPC) Inverter Topology, IEEE, Tran. Industry Application, 1992, Vol. 28, No.3, p. 558-566.
8. Gyugi L., Unified Power-Flow Control Concept for Flexible AC Transmission Systems, IEE. Proced. C, 1992, Vol. 139, No.4.
9. Holtz J., Pulse Width Modulation - A Survey, IEEE Trans. On IE., 1992, Vol. 39, No. 5, p. 410-420.
10. Cho G.C., Choi N.S., Rim C.T., Cho G.H., Modeling, analysing and control of static var compensator using three-level inverter, IEEE ind.Soc.Annu.Meet., 1992, p. 837-843.
11. Liu H.L., Cho G., Park S.S., Optimal PWM Design for High Power Three-level Inverter through Comparative Studies, IEEE Transaction on Power Electronics, 1995, Vol.10, No. 1.
12. Cho G.C., Jung G.H., Choi N.S., Cho G.H., Analysis and Controller Design of Static Var Compensator Using Three-Level GTO Inverter, IEEE Trans. Power Electron, 1996, Vol. 11, No. 1.
13. Draou A., Benghanem M., Tahri A., Performance Analysis of Advanced Static VAR Compensator using Three-Level IGBT Inverter, IEEE/ IECON, San Jose, California, USA November 29-December 3, 1999, p. 1440-1444
14. Benghanem M., Draou A., Tahri A., A New Technique of Harmonics Elimination Method Applied to an N.P.C Topolgy Three Level Inverter, International Conference on Communication, Computer & Power (ICCCP’01) Muscat Sultanate of Oman, February 12-14, 2001.