A Comparative Modelling Study of PWM Control Techniques for Multilevel Cascaded Inverter
A. TAHRI, A. DRAOU
Applied Power Electronics Laboratory, Department of Electrotechnics, University of Sciences and Technology of Oran, BP 1505 El Mnaouar (31000 Oran), Algeria, Fax: +21341421581
Dr. Azeddine DRAOU, Senior member IEEE, adraou@yahoo.com
Abstract
The emergence of multilevel converters has been in increase since the last decade. These new types of converters are suitable for high voltage and high power application due to their ability to synthesize waveforms with better harmonic spectrum. Numerous topologies have been introduced and widely studied for utility and drive applications. Amongst these topologies, the multilevel cascaded inverter was introduced in Static Var compensation and drive systems.
This paper investigates several control techniques applied to the Multilevel Cascaded Inverter in order to ensure an efficient voltage utilization and better harmonic spectrum. A modelling and control strategy of a single phase Multilevel Cascaded Inverter is also investigated. Computer simulation results using Matlab program are reported and discussed together with a comparative study of the different control techniques of multilevel cascaded inverter.
Moreover, experimental results are carried out on a scaled down prototype to prove the effectiveness of the proposed analysis.
Keywords
PWM, Multilevel inverter, Cascaded, NPC, Harmonics
Introduction
Recently the multilevel pulse width modulation (PWM) converter topology has drawn tremendous interest in the power industry since it can easily provide the high power required for high power applications for such uses as static VAR compensation, active power filters, and so that large motors can also be controlled by high power adjustable frequency drives Ref. [1,2].
The multilevel voltage source inverters unique structure allows them to reach high voltages with low harmonics without the use of transformers or series connected synchronized switching devices, a benefit that many contributors have been trying to appropriate for high voltage, high power applications.
The general structure of the multilevel converter which has a multiple of the usual six switches found in a three-phase inverter is to synthesize a sinusoidal voltage from several levels of voltages, typically obtained from capacitor voltage sources Ref. [3]. The main motivation for such converters is that current is shared among these multiple switches, allowing a high converter power rating than the individual switch VA rating would otherwise allow with low harmonics. As the number of levels increases, the synthesized output waveform, a staircase wave like, approaches a desired waveform with decreasing harmonic distortion, approaching zero as the number of levels increases Ref. [4,6].
There are roughly three main types of transform less multilevel inverter topologies, which have been studied and received considerable interest from high power inverter system manufacturers: the flying capacitor inverter, the diode clamped inverter and the cascaded H-bridge inverter in Ref. [5,9]. The detailed overview and comparison of characteristics, and their implementation issues are given in our chapter in Ref. [10]. All share the same property, which is that the output filter can be dramatically reduced, and the usual bandwidth limit induced by the switching frequency can be reconsidered.
Among these inverter topologies, the flying capacitor inverter is difficult to be realized because each capacitor must be charged with different voltages as the voltage level increases Ref. [7].
Moreover, the clamped inverter, also known as a neutral clamped converter in Ref. [1] is difficult to be expanded to multilevel because of the natural problem of the DC link voltage unbalancing. It consists of two capacitor voltages in series and uses the centre tap as the neutral. Each phase leg of the three level converters has two pairs of switching devices in series. The centre of each device pair is clamped to the neutral through clamping diodes. The waveform obtained from the three level converters is a quasi-square wave output.
Though the cascaded has the disadvantage to need separate dc sources, the modularised circuit layout and package are possible and the problem of the dc link voltage unbalancing does not occur, thus easily expanded to multilevel. Due to these advantages, the cascaded inverter bridge has been widely applied to such applications as HVDC, SVC, stabilizer, high power motor drive and so on. This topology of inverter is suitable for high voltage and high power inversion because to its ability to synthesize waveforms with better harmonic spectrum and low switching frequency Ref. [9].
This paper will investigate several control techniques applied to the multilevel cascaded inverter in order to ensure an efficient voltage utilization and better harmonic spectrum [8]. Computer simulation results with MatLab will be presented and discussed together with a comparative study of the different control techniques Ref. [11].
Moreover, the mathematical model of a 7 level single phase multilevel cascaded inverter is carried out using the well know mathematical model of the single phase full bridge inverter. A laboratory experimental prototype of 3 kW has been designed and constructed and tested. Some experimental results are also included in this paper for completeness.
Modelling of the Multilevel Cascaded Inverter
Figure 1 represents the structure of a three phase cascaded type converter with separate DC sources, it shows an example of an 11 level cascaded inverter composed of five full bridge inverters connected in series on each phase.. This type of converter does not need any transformer nor clamping diodes nor flying capacitors, each bridge converter generate three levels of voltages: E, 0, and E, for a three phase configuration the cascaded converters can be connected in star or delta.
It has the advantages of using fewer components and having a simple control since the converters present the same structure.
And just for completeness Fig. 2 is added which shows the power circuit of a 7 level cascaded inverter composed of three full bridge inverters connected in series on each phase.
For each full bridge inverter the output voltage is given by [5] :
![]() (1)
(1)
And the input dc current is:
![]() (2)
(2)
where:
· i =1 5 (number of full bridge inverters employed) for the 11 level cascaded type and
i =1 3 (number of full bridge inverters employed) for the 7 level type.
· Ia is the output current of the cascaded inverter.
· S1i and S2i are the upper switch of each full bridge inverter.
Now the output voltage of each phase of the multilevel cascaded inverter is given by:
![]() (3)
(3)

Figure 1. Power circuit of 11 level cascaded inverter
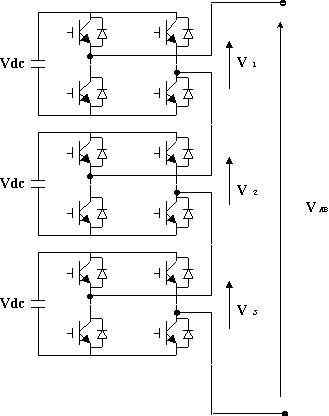
Figure 2. Power circuit of a 7 level single phase cascaded inverter
Control Techniques Used For the Multilevel Cascaded Inverter
Control strategies for the 11-th level inverter topology
Shift PWM technique
This technique uses a number of wave carriers equal to the number of full bridge inverters employed in the cascaded inverter structure shifted by 1/(5.fc), where 1/fc is the period of carrier reference [4].
In this technique the frequency modulation index is always multiple of three to have a symmetry in the output voltages. Fig. 3 shows The SPWM technique for the 11-th level cascaded inverter and the output voltage is depicted in Fig. 4. Fig. 5 shows the output voltage spectrum of the 11-th level cascaded inverter for different frequency modulation index mf.
In three phase system the frequency modulation index is defined as:
![]() , with mf =3, 6, 9,
. (4)
, with mf =3, 6, 9,
. (4)
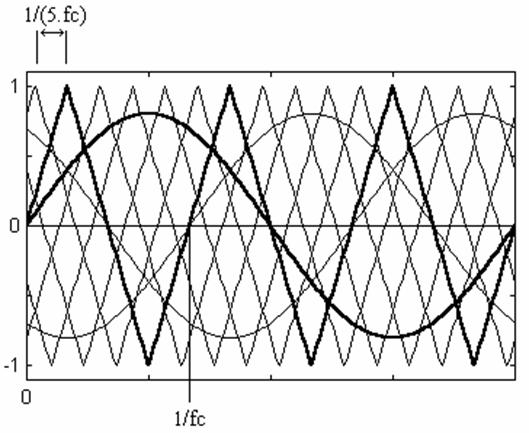
Figure 3. 11 level cascaded inverter shift
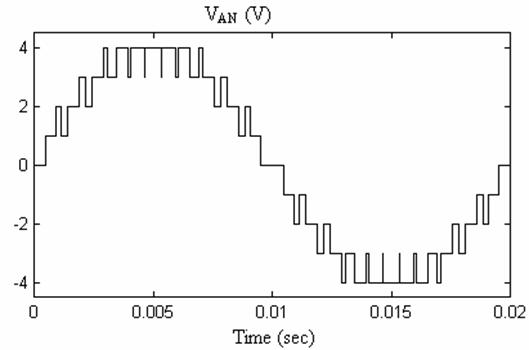
Figure 4. Line to neutral output voltage PWM for mf =3 of 11 level technique cascaded inverter
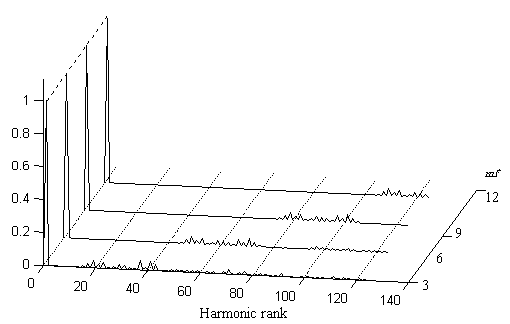
Figure 5. Output voltage spectrum of 11 level cascaded inverter for mf =3, 6, 9, 12
Sinusoidal Natural PWM (SNPWM) technique
Sinusoidal pulse width modulation is one of the primitive technique which was expanded to the multilevel (here 11 level) cascaded inverter as shown in Fig. 6.
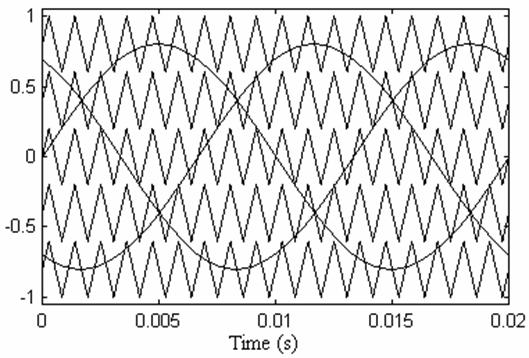
Figure 6. References and carriers
Fig. 7 shows the output voltage with SNPWM technique for mf=3 and n=5 for the same 11 level inverter.
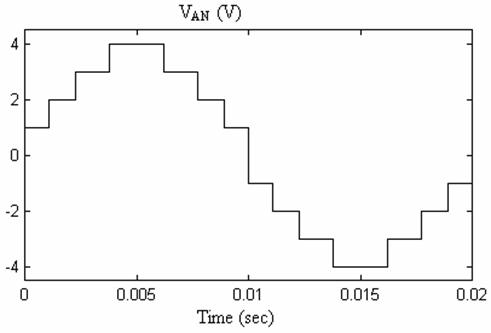
Figure 7. Line to neutral output voltage waveforms
Fig. 8 shows that for the same mf, the output voltage spectrum of SPWM technique is better than that of SNPWM technique. The SNPWM can be used for very high power application which needs low stress on power devices as IGBTs.
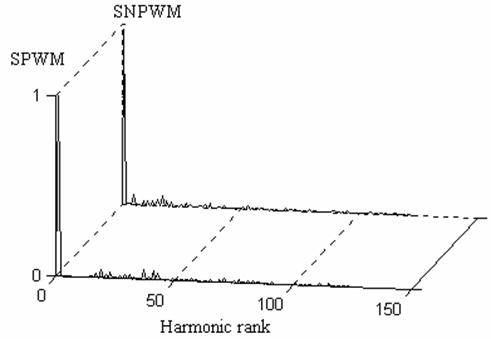
Figure 8. Output voltage spectrum of both PWM technique for mf = 3.
Programmed PWM technique
Programmed PWM technique allows the elimination of selected number of harmonics. This method is used because it optimises a particular objective function such as to obtain minimum losses, reduced torque pulsations, selective elimination harmonics, and therefore is the most effective means of obtaining high performance results.
With the equal amplitude of all dc sources, the expression of the amplitude of the fundamental and all harmonics contents are given by:
![]() , for odd n (5)
, for odd n (5)
![]() , for even n (6)
, for even n (6)
where Vdc is the dc voltage supply, and m is the number of dc source and ak is the optimized harmonic switching angles.
The low-order surplus harmonics must be eliminated; therefore equation (5) shows that m-1 odd harmonics and m-1 non triplen odd harmonics can be eliminated. The parameters of the programmed PWM can be found by the resolution of the set of nonlinear equations given by equations (5) and (6).
Table.1 gives the switching angles of the programmed PWM for different modulation index (MI).
Table 1. Switching angles
|
MI |
α1 |
α2 |
α3 |
Α4 |
α5 |
|
0.5 |
36.68 |
50.19 |
65.39 |
82.69 |
91.25 |
|
0.6 |
35.34 |
46.95 |
58.57 |
72.61 |
87.83 |
|
0.7 |
34.37 |
44.62 |
54.14 |
65.37 |
77.91 |
|
0.8 |
22.34 |
39.27 |
52.68 |
59.31 |
70.96 |
Fig. 9 shows the output voltage with Programmed PWM technique for MI = 0.5, and fig. 10 illustrates the output line to line voltage spectrum for the same MI for the 11 level inverter.
This control technique of multilevel cascaded inverter gives good performances and the output voltage spectrum is better when the number of full bridge inverter used increases.
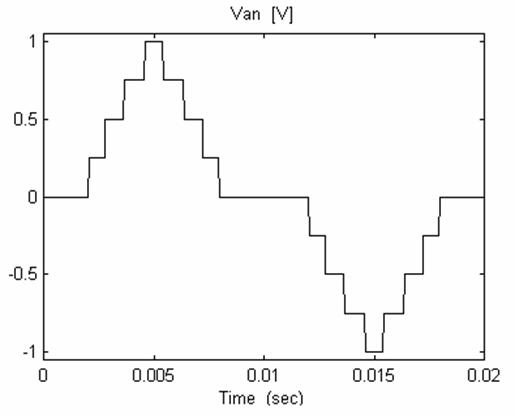
Figure 9. Line to neutral output voltage
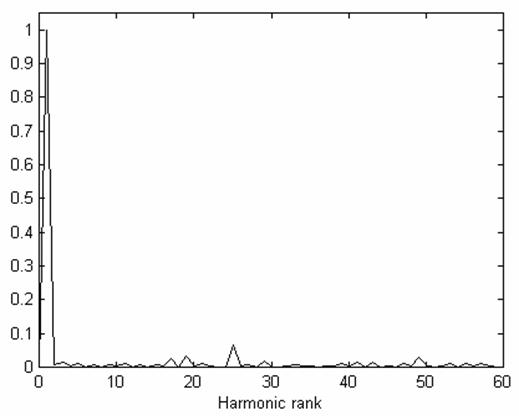
Figure 10. Output voltage spectrum
Control strategy for the7 level inverter topology
The PWM technique which control the single phase cascaded inverter employs a number of wave carriers equal to the number of full bridge inverters used in this cascaded topology structure.
In this PWM technique so-called Shift PWM, the carriers signal are shifted by 1/(3.fc), where 1/fc is the period of carrier reference [4], [5].
The parameters of SPWM technique are defined as amplitude modulation index ma and the frequency ratio mf:
![]() ,
, ![]() (7)
(7)
where Am is the peak to peak amplitude of the reference or modulation waveform and fm is its frequency. fc is the frequency of the carrier signal.
Figure 11 shows the SPWM technique for 7 level cascaded inverter for ma = 0.8 and mf = 2.
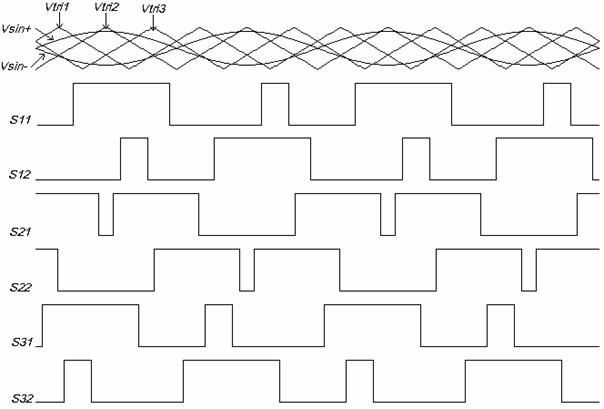
Figure 11. SPWM Technique for a 7 level cascaded inverter
Fig. 12 shows the output voltage of each full bridge inverter and the output voltage of the multilevel inverter for ma = 0.8 and mf = 2.
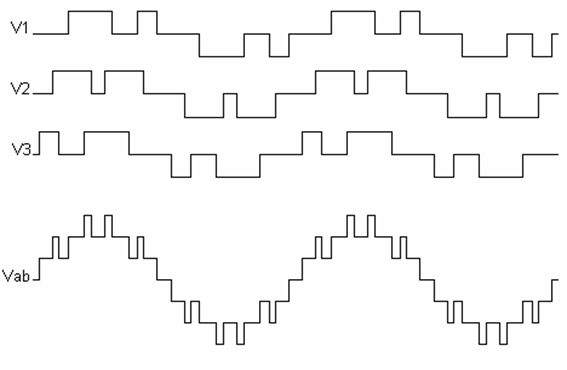
Figure 12. Output voltages of a 7 level single phase cascaded inverter
Simulation and Experimental Results
To verify the modelling and analysis of the control techniques used for the multilevel cascaded inverter, a 3 kW prototype of a 7 level single phase cascaded inverter was built in laboratory as pictured in Fig. 13.
Fig. 14, 15 and 16 show the output voltage of each full bridge inverter of the 7 level single phase multilevel cascaded inverter prototype for ma = 1 and mf = 2. Fig. 17 shows the output voltage of the 7 level single phase multilevel cascaded inverter.
Fig. 18 and 19 show the output voltage of the 7 level multilevel cascaded inverter for ma = 1 and mf = 6 and mf = 12 respectively.

Figure 13. Experimental prototype of a 7 level single phase cascaded inverter
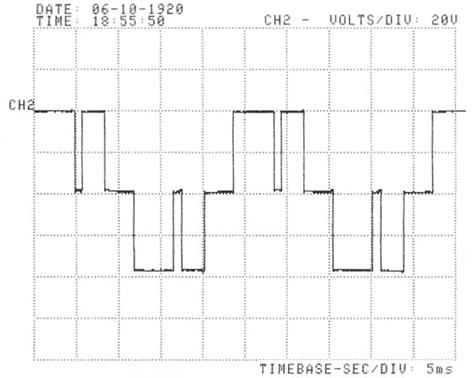
Figure 14. Output voltage of the first full bridge inverter for ma = 1 and mf = 2
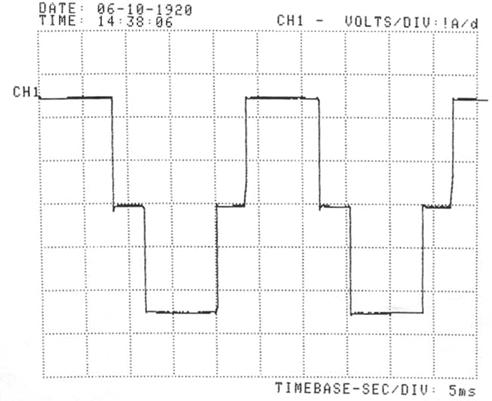
Figure 15. Output voltage of the second full bridge inverter; ma = 1, mf = 2
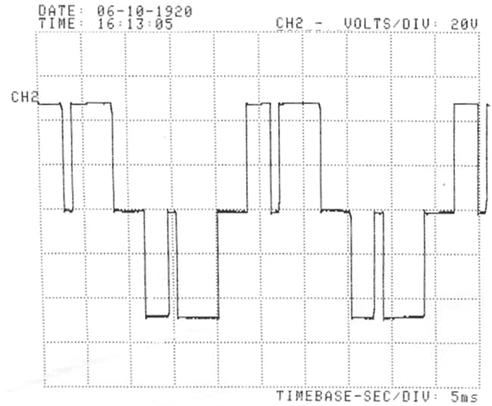
Figure 16. Output voltage of the third full bridge inverter for ma = 1 and mf = 2
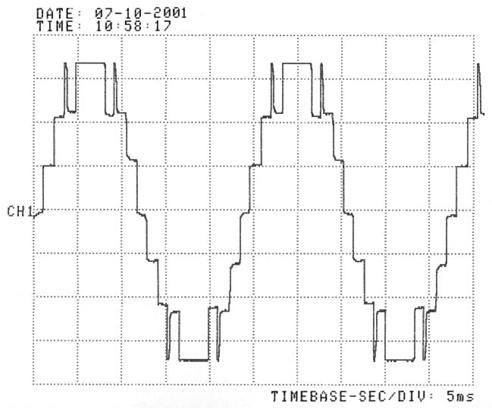
Figure 17. Output voltage of the 7 level single phase cascaded inverter; ma = 1, mf = 2
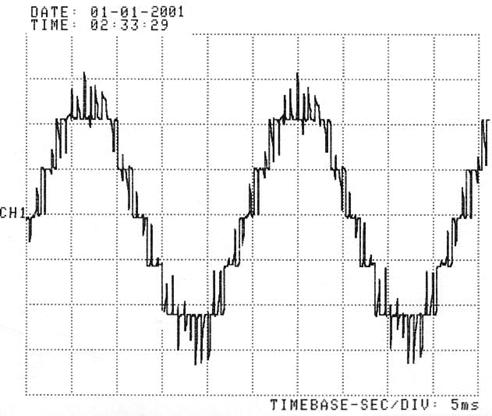
Figure 18. Output voltage of the 7 level single phase cascaded inverter; ma = 1, mf = 6
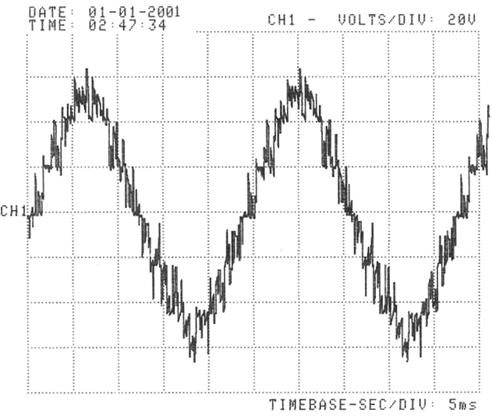
Figure 19. Output voltage of the 7 level single phase cascaded inverter; ma = 1, mf = 12
Conclusions
It has investigated the performance of various techniques in terms of output voltage spectrum. It is possible to obtain a satisfactory spectral performance with relatively low switching frequency. It has been shown that the SNPWM technique gives poor output voltage spectrum than the SPWM technique, but the programmed PWM is the best one for many applications that need high dynamic performance in high power application. Moreover, comparative simulation analysis between the different multilevel cascaded inverter control techniques is provided.
It has also investigated the modelling and control of a 7 level single phase multilevel cascaded inverter. Finally, experimental results on a small prototype are reported to prove the effectiveness of this topology of inverter.
References
1. Nabae A., Takahashi I., Agaki H., A New Neutral-Point-Clamped PWM, Inverter, IEEE Transactions on Industry Applications, Vol. IA-17, No. 5, Sep.-Oct., 1981, p. 518-523.
2. Bhagwat P.M., Stefanovic V.R., Generalized Structure of a Multilevel PWM Inverter, IEEE Transactions on Industry Applications, Vol. IA-19, No. 6, Nov.-Dec., 1983, p. 1057-1069.
3. Enjiti P.N., Jakkli R., Optimal Power Control Strategies for Neutral Point Clamped (NPC) Inverter Topology, IEEE, Tran. Industry Application, vol. 28, no.3, May-June 1992, p. 558-566.
4. Gyugi L., Unified Power-Flow Control Concept for Flexible AC Transmission Systems, IEE. Proced. C, Vol. 139, No. 4, July 1992, p. 323-331.
5. Peng F.Z., Lai J.S., Multilevel Converters - A New Breed of Power Converters, IEEE Transactions on Industry Applications, Vol. 32, No. 3, May-June 1996, p. 509-517.
6. Joos G., Huang X., Ooi B.T., Direct-Coupled Multilevel Cascaded Series VAR Compensators, Proc. of IAS97, 1997, p. 1608-1615.
7. Hochgraf C., Lasseter R., Divan D., Lipo T.A., Comparison of Multilevel Inverters for Static Var Compensation, Proc. of IAS98, 1998, p. 921-928.
8. Toblert L.M., Peng F.Z., Habetler T.G., Multilevel PWM Methods al low Modulation Indices, APEC99, Dallas, Texas, March 14-18, p. 1032-1039.
9. Draou A., Benghanem M., Tahri A., Performance analysis of advanced Static VAR Compensator using three level inverter, Conf. Rec. IEEE/IECON99, USA, Nov. 1999.
10. Teodorescu R., Blaabjerg F., Pedersen J. K., Cengelci E., Sulistijo S.U., B. O. Woo and P. Enjeti, Multilevel Converters A survey, EPE99 Lausane, 1999.
11. Rashid M.H., Power Electronics handbook, Academic Press, Aug. 2001.
12. Tahri A., Draou A., Benghanem M., PWM Control Techniques for Multilevel cascaded Inverter, Second International conference on Electrical and Electronics Engineering, ELECO2001, Bursa, Turkey, 7-11 November 2001.