Mathematical Modeling of a Simulated Fixed Bed for Desalting Operation
MOHAMMED ALHASSAN and M. A. OLUTOYE
Department of Chemical Engineering, Federal University of Technology, Minna, Nigeria
Abstract
Continue survival of the petrochemical industry in the face of advancement in processing technology must change for better performance. In doing so, the pre-treatment stage of crude, which include desalting will go a long way at improving the overall quality of the product obtained. It is in view of this that a mathematical modeling of adsorption of a fixed simulated bed for desalting operation was carried out to determine the variation of the concentration of adsorbate (mol/l) and the amount of adsorbate (mol) of the simulated fixed bed, using a prototype simulated fixed bed, and Silica – Alumina as the adsorbent. A model equation was developed from the prototype .both the model and simulated results showed that the concentration of the effluent stream decreases as the height increases down the column, giving effective absorbate absorption, until the concentration reaches 2.48 mol/l, while the amount of the absorbate increases down the depth of the column to an amount 28.29 mol, The optimum height for the adsorbent bed design obtained was approximately 5.67m, while the graphical analysis of the experimental and the simulated results showed that there is a close agreement between them. The results obtain is suitable for desalting operation and for research and development of the existing plants, and can be used in building of pilot scale to the plant stage.
Keywords
Modeling, Simulation, Fixed bed, Desalting operation, Q-basic programs, Absorbate, Absorption, Silica - alumina.
Introduction
Development enhanced by innovation in technology to man have been rather periodic. From the Stone Age to the Iron Age, to the Bronze Age and now the Computer Age and the Age of Artificial Intelligence. Man had to be swept by changes in technology. Today’s man is engulfed with the considerable excitement from the dividend he derives from oil refining, fuel and lubricating industries. Advances in technology of crude oil processing have prompted new products that are fast replacing the traditional materials for better performance and are creating a lot of new application. Advancement in processing technology worldwide has increased; demanding new and improved tools and process equipment. These have not only improved the standard of living and life expectancy, but have contributed significantly to the success achieved in the various sectors of our national life. With the fuel oil, lubricating industries can now produce a wide range of Petrochemicals, which include the Polyethylene used for making our disposable hand bags, Vinyl resins, solvents, lead tetraethyl used for improving petrol (pms) octane rating and burning characteristic, Refrigerants, synthetics, detergents, just to mention but a few [1].
For the continue survival of the petrochemical industry, in the face of advancement in processing technology, our technology must also change for better performance variant. In doing so, the pre-treatment stage of crude, which include desalting will go a long way at improving the overall quality of the product obtained. It is in the light of this trend, that a mathematical modeling of adsorption of a fixed simulated bed for desalting operation was carried out. The results obtain is suitable for desalting operation and for research and development, can be built from the pilot scale to the plant stage. A combine effort of both the industry and academic for strategic research and development will help to become fully aware of the problem, prospects and get challenged for sustainable development [2].
Adsorptions from the liquid phase have long been used for removal of contaminants present at low concentrations in process streams. In some instances, the objective is removal of specific compounds [3]. In the case of this work, the main objective is the removal of basic salts, which include NaCl, KCl, CaCl2 and organometallic impurities from crude oil. In others, the contaminants are not well defined, and the objective is the improvement of general properties such as colour, taste, and odour and storage stability [4, 5]. The first know commercial acceptance of adsorption over other separation technique is the Sorbet technology. These technology have not, however met the demand for it usage in the case of crude oil pre-treatment before distillation. With continuous research and development the fixed adsorbent bed and simulated for other beds can be fully exploited in usage for crude pre-treatment [6]. The designed simulated adsorbent bed uses Zeolite-alumina adsorbent for the removal of the salts defined. Its advantage includes the fact that adsorption offers a more efficient route to this method of separation of commercial interest than do the desalting method using electro dialysis. This stems in part from the fact that adsorbents are know silica-alumina that are much more selective in their affinity for the materials to be removed, basic salts than are any known solvents (the emulsifier used in the desalting equipment).
Another item of comparable importance in the used of the fixed adsorbent bed and simulated fixed beds is the fact that much higher efficiency is obtained from these beds than in the conventional desalting equipment, using the method of electro dialysis. This is as a result of the use of small particles adsorbent “silica - alumina” to give high interfacial area and from the absence of significant axial mixing of either phases [6]. How ever this is in contrast to the desalting equipment designed to obtain practically complete axial mixing in each physical element.
Aim of the Research Work
The aims of this research work are:
· Mathematical modeling of a fixed simulated bed for desalting operation;
· To determine the optimum depth of an adsorption column needed for a satisfactory adsorption of the adsorbate from the effluent stream;
· Determine the best adsorbent for the operation of fixed simulated bed;
· Derive and alternative and cheap processing method of desalting;
· To encourage the use of mathematical modeling in areas where design data are not sufficient or limited the design and construction of adsorption equipment and laboratory prototypes.
Limitation of existing technology:
· The quality of crude charged to the desalter affects the desalting efficiency;
· Normally, light density (low) crude is relatively easy to desalt than the heavy (high) density crude oils for the following reasons;
o The differential density between the crude and H2O is small;
o Heavier tend to contain more naturally occurring emulsifier than do lighter ones;
o Heavier crude’s often contain more sulphur and hence more iron sulphide. Where iron sulphide is present, it is insoluble in both oil and water and tend to accumulate at the oil / H2O interface;
· The presence of slope oil will typically contain high levels of metal additives from tube oils, sand, silt and a variety of other contaminants. As a result emulsion breaking is often difficult to accomplish. The inclusion of slop naphtha in crude feeds containing asphaltic crude or heavy fuel oil can also give rise to desalting problems, notably dissolved effluent H2O;
· Raw crude quantity. Since the desalting process is largely a physical and dynamic function, their velocity and residence time will affect performance. Though put changes will affect flow character;
· The wash water obtained from the desalter is often of pH 5.7 range. The injection of caustic soda to raise the pH may results to severe desalter problem due to emulsion stabilization [5].
Literature Review
The Rational For Mathematical Modelling
A model is nothing more than mathematical abstraction of a real process. The equation or sets of equations that comprise the model are best an approximation to the true process. Hence, the model cannot incorporate all of the features, both macroscopic and microscopic of the real process. The engineer normally must seek a compromise involving the cost of obtaining the model, that is, the time and effort required to obtain and verify it. These considerations are related to the level of physical and chemical details in the model and the expected benefits to be derived from its use. The model accuracy necessary is intertwined in this compromise and the ultimate use of model influences how accurate it needs to be. The importance of mathematical modelling of a process is from:
· To improve understanding of the process. Process model can be analysed or used in a computer simulation of the process to investigate process behaviour without the expense and perhaps, without the unexpected hazard of operating the real process. This approach is necessary when it is not feasible to perform dynamic experiments in the plant or before the plant is actually constructed.
· To train plant-operating personnel. Plant operator can be trained to operate a complex process and to deal with emergency situation by use of process simulator. By interfacing a process simulate to standard process control equipment, a realistic environment can be created for operator training without the cost or exposure to dangerous conditions that might exist in a real plant situation.
· To design the control strategy for a new process. A process model allow alternative control strategies to be evaluated such as, for example, the selection of the variables that are to be measured (controlled) and those that are to be manipulated. With more complicated processes or with new processes for which we have little operating experience, the design of an appropriate control strategy seldom is straightforward.
· To select controller settings. A dynamic model of the process may be used to develop appropriate controller settings, either via computer simulation or by direct analysis of the dynamic model. Prior to start-up of a new process, it is desirable to have reasonable estimates of the controller settings. For some operating processes, it may not be feasible to perform experiments that would lead to better controller settings.
· To design the controller. A Modern control technique often incorporates a process model into the controller. Such techniques are called model – predictive or model-based control.
· To optimise process-operating conditions. In most processing plants there is an incentive to adjust operating conditions periodically so that the plant maximizes profits and minimizes costs. A steady state model of the process and appropriate economic information can be used to determine the most profitable process conditions as in supervisory control [3].
Development of a Process Mathematical Model
Because models account more completely for what is happening in a process, fundamental model based on mass and energy balance offers better accuracy and greater insight than do regression models. Thus they are of greater value in improving process yield or through put or in debottled necking and optimising. Fundamentals models may be in existence for a long time without being used because they involved a lot of calculations and are considered difficult to develop. However, today a calculation can be done quickly and conveniently, at low cost, using an advanced computer having an arithmetic coprocessor and some graphics capability. As for building the model, there is a systematic hand-on approach that will ease the perceived development difficulties.
A model, can be developed by fitting a set of equations to actual plant or pilot plant data, and the range of these data is the range over which the model can be used. For this reason, it is important to have data that covers a fairly wide range of steady state process conditions.
In a pilot plant, such data can be collected by systematic experimentation. The experiment designed should explored high, average and low values for each of the principal process variables. Such a range of data can also be found in plant operating history. Overall, ten to twenty steady state data sets may be required. The kind of data needed to develop a mathematical model are those that define the material and energy balances around the equipment i.e., the pressure, temperature and composition of feed and product streams etc. The three major steps for building models are as follows: the first step is to develop a process flow diagram for the process. Next, is to develop a set of material and energy balance equations for the systems or around the equipment being considered and the third step is to fit the model to the data by adjusting the parameters. For large number of parameters, this step involves a number of iterations and must be done with the help of a computer. If the Mathematical model is accurate and more useful than any single material balance being written, it can be used to predict the behaviour of the process under different conditions. Then it can be used for process optimisation, supervisory control, debottlenecking and dynamic analysis.
Obviously, success in any of these areas can pay for the mathematical model development in a very short time [4].
Primary Mathematical Modeling
Fixed Simulated Bed for the Removal of Salts from Crude Oil
The model is a semi-empirical one. The mathematics of adsorption in beds i.e. the adsorption of solute from liquids on the surface of solids is either diffusion control or kinetic control. There is a fundamental difference in the mathematical analysis, depending upon whether one assumes that equilibrium obtains or whether one assumes a kinetic approach of some sort. In the first case the basic problem is in the first order partial differential equation, Since the definition of linearity for first order equations is somewhat more fearer, that, it is for second order equation from available theorem, the solution to first order term is obtained for general isotherms. This problem has been considered for possible alternatives by various researchers. For the second order case the solution is not as simple and only the solution for special cases can be solved analytically.
In finding a solution to the problem of desalting in simulated fixed bed we start thus: let us assumed we have an adsorbent bed of depth (or height) are measured as Z; then:
· Concentration in moles of a adsorbate (salts) per unit volume of solution in the crude streams be c;
· Amount of adsorbate in moles (salts) per unit volume of solution in the bed be n;
· Volume of the adsorbent bed be v;
· Where be the α fractional void volume of bed;
· Where t is the time taken for the adsorbent bed, in the primary mathematical modeling.
Then upon, considering an elemental thickness of bed Δz, we use the equation:
![]() (1)
(1)
Considering that of the local rate of removal in the bed was governed by:
![]() (2)
(2)
where N0 is the saturation capacity of the bed and k is the velocity constant. Based in the assumption in the model, we require a redistribution of the velocity constant k1 and k2, the equation (2) become:
![]() (3)
(3)
where c = c(z, t) = c0(t) where z = 0 and n = n(z, t) = n0(z) where z ≤ z/v. Changing of variables x = z/v and y = α(t-z/v) conduct to:
![]() (4)
(4)
![]() (5)
(5)
Note that:
c(z, t) = c0(y, 0) = c1(y) when x = 0 (6)
n(z, t) = n0(v, x) = n1(x) when y = 0 (7)
and hence exist a function f = f(x, y) such that:
df(x, y) = ndx - cdy (8)
Thus:
![]() ,
, ![]() (8)
(8)
Utilizing eq. (8), the equation (5), becomes:
![]() (9)
(9)
By changes of variables (re-arrangement of expression starting with known values of k1, k2, n0, c0 we get n1(x) and c1(y). The change of dependent variable:
![]() (10)
(10)
reduces to:
![]() (11)
(11)
If combine the last four equations, we obtain:
![]() (12)
(12)
![]() (13)
(13)
It follows that:
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
Starting with known values of K1, K2, n0, c0 to get n1(x) and c1(y):
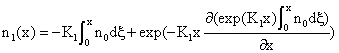 (20)
(20)
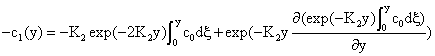 (21)
(21)
Finally:
![]() (22)
(22)
![]() (23)
(23)
Equations (22) and (23) are the model equations.
Methodology
The following materials were used:
· A prototype fixed bed for carrying out the desalting operation, it is made up of an inlet stream, an outlet stream, and a rotary device called multi port stop cock;
· Nigerian crude oil is used as the feed stock for the desalting operation (napthalene base or intermediate base, key quality 31.10 and AP10 =20.33);
· Flow rate meter; for measuring the flow rate of the crude oil, Electric weighing balance; to measure the weight of the adsorbent used and other materials used;
· Measuring cylinder Prototype fixed simulated bed for carrying out the desalting operation, the equipment for measuring the volume of the catalyst, Beakers and bottles as containers for various crude oil samples, Adsorbent made up of Silica – Alumina.
Procedure
The simulated bed was set and the crude oil passed through the bed at a controlled temperature and pressure close to atmospheric condition. From the samples obtained a recorded value of concentration changes with the depth of the bed is plotted.
Results
The result of various experiment carried out to text the model are in figures 1 to 3.
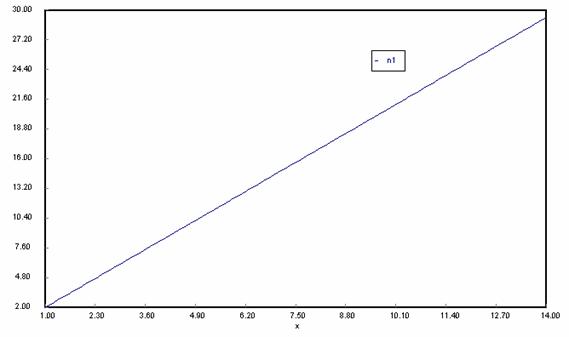
Legend: y axis – amount of adsorbate (mol); x axis – bed depth (m)
Fig. 1. Amount of Adsorbate with Depth
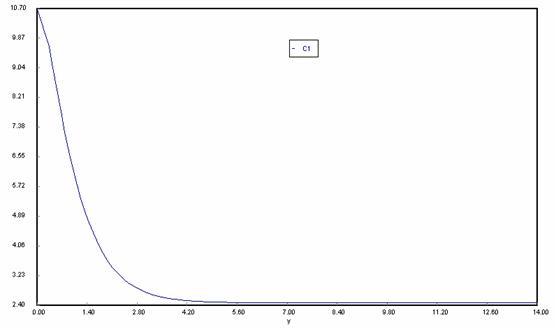
Legend: y axis – concentration of adsorbate (mol/l); x axis – bed depth (m)
Fig. 2. Concentration of Adsorbate with Depth
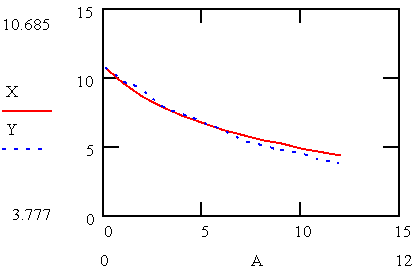
Legend: X - experimental result; Y - simulated result; A - bed depth
Fig. 3. Comparison of Simulated and Experimental Result
Discussion of Results
Mathematical modeling of a simulated fixed bed for desalting operation was carried out and the models equations developed were used in the simulation of the experimental results for desalting operation and the results obtained were discussed bellow.
Fig 1 showed that the amount of adsorbate in the bed increases as the depths of adsorption increases to a maximum value of about 29.38kmol/m3. While the concentration of adsorbate in the fluid stream decreases until it reaches a minimum value of 2.48kmol/m3 as shown in figure 2.
Fig 3 shows that the concentration of the adsorbate in the fluid stream remains practically constant at a height of approximately 14m. The mount of adsorbate in the bed increases with increase in bed depth while the concentration of adsorbate in the effluent stream decrease with depth until a minimum value of 2.4848kmol/m3 where it remain fairly constant The depth of the bed was optimum at 5.60m. And comparison between the experimental and simulated results showed that the model is acceptable within the experimental limitation.
Conclusion
A model was developed for the simulated fixed bed operation, and based on the experimental and the simulated result obtained it can be conclude that the model is fairly satisfactory since the simulated results obtained agreed with the experimental result, and that the model was can be used to determine the amount of adsorbate present in the bed and the concentration of adsorbate at any given time.
Appendix
V = volume of the adsorbate bed (dm3)
a = fractional adsorbate void volume of bed
n = adsorbate amount in moles (salts)
C = concentration (moles) of adsorbate (salt) per volume (dm3) of solution in the crude stream
Co= initial value of C
n0 = initial value of n
k1= velocity constant
t = time taken in (sec)
n1(x) = changes of n with depth
-c1(y) = changes of c wit depth
References
[1] Ahmed A. S., Modern Materials and Industrial Development of Nigeria, 27-th Annual Conference of the Nigerian Society of Chemical Engineers, Nov. 13-15, Ahmadu Bello University, Zaria, 1997.
[2] Kirk-Othmer Encyclopedia of Chemical Technology, John Willey & Sons, New York, p. 563, 1978.
[3] Breck D. W. W., Zeolite Molecular Sieves, John Willey & Sons, New York, 1974.
[4] Thomas T. L., Clark E. L., Proceedings of the 46th Annual Convention of The Natural Gas Processing Association, 1976.
[5] Crude Distillation Unit (1) Process Description Manual (Desalter), Nnpc/Krpc, Kaduna, 1978.