Control Operator for the Two-Dimensional Energized Wave Equation

 

Victor Onomza WAZIRI*, Sunday Augustus REJU

 

Mathematics/Computer Science Department, Federal University of Technology, Minna 920003, Niger State, Nigeria; *corresponding author

National Open University of Nigeria, Victoria Island, Lagos, Nigeria

dronomzawaziri@yahoo.com, sreju@nou.edu.ng

 

 

Abstract

This paper studies the analytical model for the construction of the two-dimensional Energized wave equation. The control operator is given in term of space and time t independent variables. The integral quadratic objective cost functional is subject to the constraint of two-dimensional Energized diffusion, Heat and a source. The operator that shall be obtained extends the Conjugate Gradient method (ECGM) as developed by Hestenes et al (1952, [1]). The new operator enables the computation of the penalty cost, optimal controls and state trajectories of the two-dimensional energized wave equation when apply to the Conjugate Gradient methods in (Waziri & Reju, LEJPT & LJS, Issues 9, 2006, [2-4]) to appear in this series.

Keywords

Conjugate Gradient method (CGM), Extended Conjugate Gradient Method (ECGM), Convolution integral, Control operator, Hilbert space, Integral quadratic objective function

 

 

Introduction

The energized wave equation is a euphemism of wave with diffusion and source effects. The constraint equation is generally a combination of wave and heat (energy) with a source. It has the understated physical configuration:

                           (1)

where c2 and d are defined as the speed of propagation and diffusivity in a recognized medium. Henceforth, to simplify computational burden, the two defined terms assume unity. Thus, the wave part of equation (1) is

                                                                       (2)

while the energy or diffusion effect configuration is:

                                                                         (3)

The term u(x,y,t) is the source (negative source), which controls some inflows at some control demand; say into the medium of propagation.

This research is geared towards obtaining the operator that would enable complete the stability, controllability and observability of the dynamical system of equation (1).

In this work, results retain their partial differential forms and we intent to get them solved analytically in their time and space variables. In other words, the control operator retains three independent variables (time t and the two space variables x and y).

 

 

Modelling the Problem

 

Problem P1

Our optimization problem P1 is modelled in according with the formulation of Waziri [5].  The model of the two-dimensional energized wave equation is:

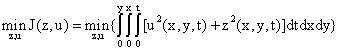                                               (4)

subject to the dynamical constraint:

                                                           (5)

with initial and boundary conditions:

                                                         

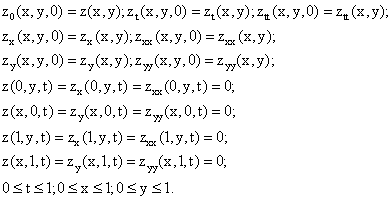
These initial conditions shall for usefulness in the construction of the inverse Laplace transform in the derivation of the ECGM control operator.

 

Problem P2

To optimize the integral quadratic problem P1, we have to construct an unconstrained equation by penalizing the dynamical constraint equation (4) with a cost functional μ(x,y,t) ≥ 0. The unconstraint equation is defined hereunder as:

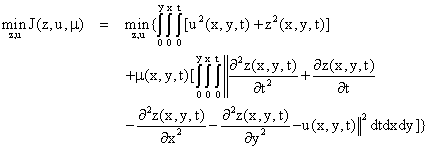                        (6)

Equation (6) in bilinear Hermitian form yields:

 

Problem P3

                                                                            (7)

where w = (w1, w2) and equation (7) denotes an inner product space expressible as:

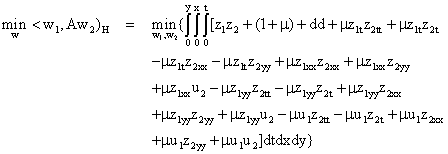                    (8)

It is important to note that the control operator associated with the penalized functional (8) is equivalent to that associated with its Bilinear Hermitian form (7); and equivalence is preserved under the following equivalent laws:

z1 = z2 = z; z1t = z2t = zt; z1tt = z2tt = ztt; z1xx = z2xx = zxx; z1yy = z2yy = zy; u1 = u2 = u

The Bilinear Hermitian form (7) is conveniently written compactly as:

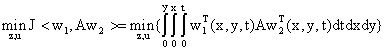                                    (9)

The H appearing in equation (9) symbolizes a Hilbert space which is defined as: H = w22[0,1][0,1]*l22[0,1][0,1], where “*” is a multiplicative operator. The term w22[0,1][0,1] is a Sobolev space of absolutely continuous functions X(∙,∙,t) squared integrable over the surface space [a,b][c,d], while l22[0,1][0,1] is the Hilbert space of equivalence classes of real valued functions on the surface [a,b][c,d].

The operator A in equation (9) is associated with equation (8) which is a squared symmetric positive definite, linear inner product operator defined equivalently:

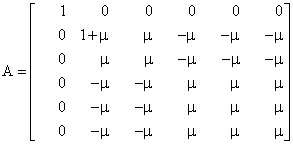
In the computational processes, the control operator A is not fixable for our integral quadratic objective functional posed by problem P1. We need a new operator that would be compatible to our problem. Hence, we must redesign the new control operator in line of the development from [6]. Let the new control operator be recognized as B which has the same Hilbert space property as defined on the control operator A and satisfies the Bilinear Hermitian form.

 

 

Derivation of the ECGM Fundamental First Fourth Order PDE

 

In constructing the new control operator (otherwise known as the ECGM operator that would replace the old operator A), we replace A with B in equation (8) such that:

 

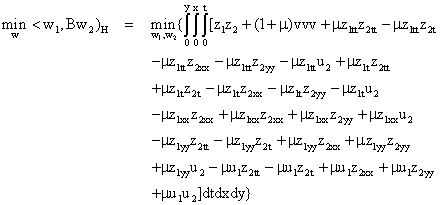                      (10)

In a more compact format, equation (10) can be rewritten as:

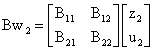                                                                                              (11)

We obtain B11 and B21 by setting u2 = 0; in the same vein, set z2 = 0 to obtain B12 and B22. Now by setting u2 = 0, equation (11) reads:

Thus with u2 = 0, equation (10) reads:

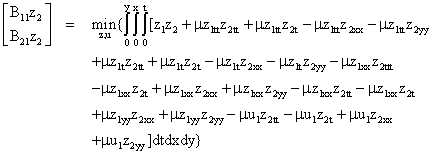                                    (12)

Upon simplifying, equation (12), we have:

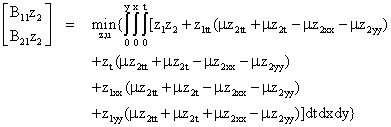                                  (13)

On the strength of Gelfand and Fomin Lemma ([7], which we reproduce here in term of our dimensional case), equation (13) can be solved.

 

Lemma (Gelfand-Fomin)

If φ(x,y,t) and ψ(x,y,t) are continuous functions in closed region [a,b][c,d]:

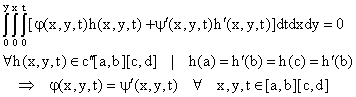                                           (14)

In view of Lemma, reconsider equation (14) such that:

γ = z2; α = μz2tt + μz2t - μz2xx - μz2yy; β = -α

We rewrite equation (14) and with the boundary assumption [x,y,t] = [1,1,1] as inherited from the posed problem P1:

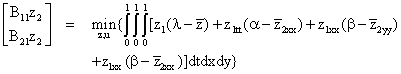                                (15)

From equation (14), set:

                                                                                              (16)

Invoking the Gelfand-Fomin (Lemma, ibid [7]), we must therefore have that the two embedded  factors in equation (15); (α-), (β-), and (β-) are continuous functions on the interval [0,x][0,y] and are continuously differentiable on the interval [0,1][0,1]; also they are  equipped with a normed space such that:

where y(n) is the n-th differential of  y = y(ζ) = [x,y,t] Î [0,1][0,1]

Thus (α-), (β-), and (β-) are continuously partial differentiable functions such that:

                                                                             (17)

Hence (17):

                                                                                                                        (18)

Equation (18) resolves into the form:

                                                                                                                      (19)

But α = - β by symmetric definition; therefore equation (19) is rewritten as:

                                                                                                                                       (20)

which is expressible uniquely as:

                                                            (21)

Thus, it is not difficult to see that equation (21) yields:

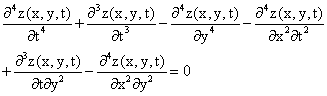                                                                          (22)

 

The derivation of the ECGM fundamental second fourth order PDE

The second ECGM fourth order partial differential equation is obtained by setting z2 = 0 in equation (13) such that:

                                                                                                            (23)

By putting z2 = 0, equation (10) becomes:

                                 (24)

Let α - μu2tt(x,y,t) and β - μu2yy(x,y,t) be continuous and continuously differentiable over the space region [0,1][0,1]. Therefore invoking the Gelfand-Fomin algorithm and after some due analytical simplification processes as in previous section, we obtained the second fourth order partial differential equation:

                                                    (25)

From equation (23), we deduced the element operator B12:

                        B12 = (1+μ)u2(x,y,t)                                                                                                      (26)

We will in the next section solve equations (22) and (26) using the initial and boundary conditions as inherited from problem P1.

 

Solving the first and second fourth order PDE

We now solve the fourth order partial differential equation (22). By taking the Laplace transform of equation (22) with respect to t-variable and considering the initial conditions as stipulated from the original problem P1, we have the transformation:

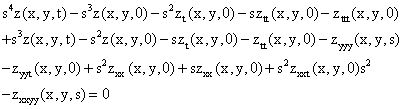                               (27)

Taking the Laplace transform further with respect to y and x variables, equation (27) becomes:

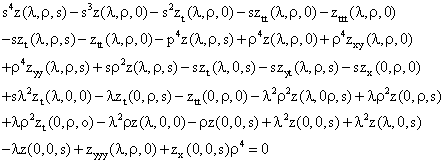                     (28)

Considering the initial and boundary conditions, equation (5.2) is expressible as:

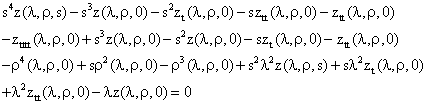                        (29)

Dividing all terms in equation (29) by λ2ρ4s4 yields:

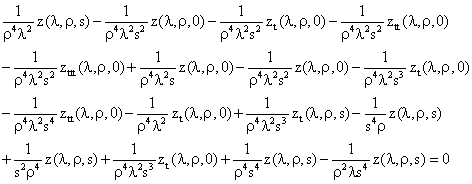                                      (30)

The inverse Laplace transforms with respect to each of the energized wave independent space variables and time t are considered. Nonetheless, worthy to consider are some vital propositions credited to (Reju, 1995 [8]); shall form useful tools in the derivation of the inverse Laplace transform of equation (30).

The prepositions:

·        Preposition 1

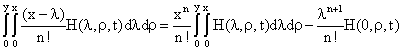
·        Preposition 2

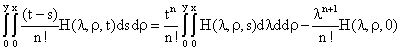
·        Preposition 3

·        Preposition 4

Using the four stated preposition appropriately, the inverse Laplace transform to equation (30), and then differentiating equation with respect to t-variable and simplifying results, we obtain the element control operator B11 defined hereunder (B11(x,y,t) = z(x,y,t)):

                                    (31)

 

                                    (31)

 

 

Solution of the Second Fourth Order PDE

 

Reconsider equation (25) and taking the Laplace transform of each independent variables x, y and t of equation (25) and differentiating the result with respect to t, yields:

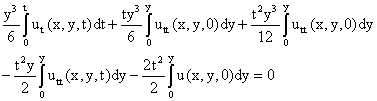                                                              (32)

By re-arranging equation (32) component-wise for the control operator B22, we obtained:

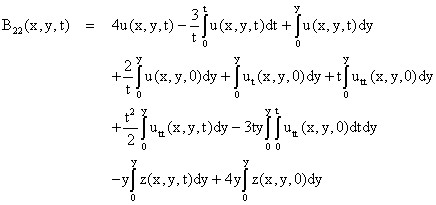                       (33)

 

 

Summary for the Control Operator

 

We give summary of the analytical control operator hereunder:

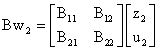                                                                                                                    (34)

wherein w2 = (z2, u2).  

The summary of the control operator components are obtainable by referring to the following listed equations. Equations (16), (26), (31) and (33) constitute the control operator when substituted into equation (34). The substituted components completely define the control operator that would replace the analytical operator A in the implementation of the ECGM algorithm. In fact, the control operator B differs remarkably from the operator A obtained in section Modelling the Problem in that while the former is completely expressed in matrix term of state variables and time, the latter is a matrix constant.

 

 

Conclusion

 

The control operator has been derived for the two-dimensional energized wave equation. The operator shall form the framework in the derivation of the optimal control and state trajectories numerical values using the conjugate gradient algorithm as formulated.

References

 

[1]        Hestenes M. R., Stiefel E, Method of conjugate Gradient Method for solving linear systems, J. Res. Nat. Bureau Standards, 49, p. 409-36, 1952.

[2]        Waziri V. O., Reju S. A., Implementation of the Extended Conjugate Gradient Method for the Two-Dimensional Energized Wave equation, Leonardo Electronic Journal of Practices and Technologies, Romania; ISSN 1583-1078, Issue 9, July-December, p. 33-42, 2006.

[3]        Waziri V. O., Reju S. A, The Analysis of the Two-dimensional Diffusion Equation With a Source, Leonardo Electronic Journal of Practices and Technologies, Romania,  ISSN 1583-1078. Issue 9, July-December, p.43-54, 2006.

[4]        Waziri V. O., Reju S. A., The Penalty Cost Functional for the Two-dimensional Energized Wave Equation. Leonardo Journal of Science, Romania,  ISSN 1583-0233, Issue 9, July-December, p. 45-52, 2006.

[5]        Waziri, V. O., Optimal Control of Energized Wave equations using the Extended Conjugate Gradient Method (ECGM), Ph.D. Thesis, Federal Univ. of Technology, Minna, Nigeria, 2004.

[6]        Ibiejugba M. A., Onumanyi P., On control operator and some of its applications, J. Math. Analy. Applic., 103, p. 31-7, 1984.

[7]        Gelfand I. M., Fomin S. F., Calculus of Variations, Prentice Hall Inc., Eaglewood Cliffs, New Jersey, 1963.

[8]        Reju S. A., Computational Optimization in Mathematical Physics, Ph.D. Thesis, Univ. of Ilorin, Ilorin, Nigeria, 1995.