The Penalty Cost Functional for the Two-Dimensional
Energized Wave Equation
Victor Onomza WAZIRI1, Sunday Augustus REJU2
1Mathematics/Computer Science department, Federal university of Technology, Minna 920003, Niger State, Nigeria; 2National Open University of Nigeria, Victoria Island, Lagos, Nigeria; dronomzawaziri@yahoo.com, sreju@nou.edu.ng
Abstract
This paper constructs the penalty cost functional for optimizing the two-dimensional control operator of the energized wave equation. In some multiplier methods such as the Lagrange multipliers and Pontrygean maximum principle, the cost of merging the constraint equation to the integral quadratic objective functional to obtain an unconstraint equation is normally guessed or obtained from the first partial derivatives of the unconstrained equation. The Extended Conjugate Gradient Method (ECGM) necessitates that the penalty cost be sequentially obtained algebraically. The ECGM problem contains a functional which is completely given in terms of state and time spatial dependent variables.
Keywords
Penalty functional, energized waves, Control operator, Optimal control, optimal control and ECGM
Introduction
We now define the statement of the two-dimensional problem in a characteristic dexterity as in [[1]]: Problem (P1):
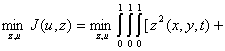
![]() 1.1
1.1
subject to the energized wave equation:
![]() 1.2
1.2
with initial and boundary conditions:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The unconstraint problem of the two-dimensional energized wave equation is defined as: Problem (P2)
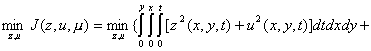
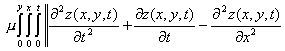
![]() 1.3
1.3
In solving equation (1.1), we will need the numerical value of the
penalty cost constant![]() . To achieve this, we must derive a
penalty functional in state variables such that
. To achieve this, we must derive a
penalty functional in state variables such that![]() . Thereafter, we shall obtain
the program codes for some optimal numerical values at different state profile
strata. The control
. Thereafter, we shall obtain
the program codes for some optimal numerical values at different state profile
strata. The control ![]() and state
and state ![]() partial derivatives are
equivalently derived by the Hamiltonian form akin to [1] and [[2]] as follows:
partial derivatives are
equivalently derived by the Hamiltonian form akin to [1] and [[2]] as follows:
![]()
![]()
![]()
![]() 1.4
1.4
In a further development, since the rate of change of the optimal control is the state, then:
![]()
![]()
![]()
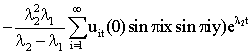 1.5
1.5
Differentiating equation (1.5) further with respect to time t:
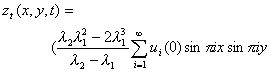
![]()
![]()
![]() 1.6
1.6
Also equation (1.6) further derivative yields:
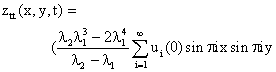
![]()
![]()
![]() 1.7
1.7
Differentiating the state equation with respect to x twice:
![]()
![]()
![]() 1.8
1.8
Also differentiating the state equation with respect to y twice results in:
![]()
![]()
![]() 1.9
1.9
The derived equations (1.3) through to (1.9) are useful tools in the implementation of the ECGM algorithm once the control operator is ready.
The construction of the penalty cost functional
In the follow-up and in light of the derivation in [[3]]
control operator, we construct the penalty cost functional for the
two-dimensional energized wave equation. By definition, we assumed that the
optimal control operator ![]() obtained for the two-dimensional case are
symmetric positive definite; hence comparably equivalence. In the control
operator, we obtained these:
obtained for the two-dimensional case are
symmetric positive definite; hence comparably equivalence. In the control
operator, we obtained these:
![]()
![]() 2.1
2.1
![]() 2.2
2.2
It is not difficult to see that equations (10) and (11) are equivalently expressed as:
![]() 2.3
2.3
Based on Reju [2], the action of the analytical state on the space variables ![]() can be
conveniently be expressed as:
can be
conveniently be expressed as:
![]()
![]() 2.4
2.4
It is easy to express equation (2.4) in this order:
![]() 2.5
2.5
where
![]() 2.6
2.6
From equation (2.6), we observe that the penalized parameter is dependent
on the state ![]() and its partial derivatives which are in
themselves dependent on the spatial variables x and y with time t. It is
obvious that the parameter
and its partial derivatives which are in
themselves dependent on the spatial variables x and y with time t. It is
obvious that the parameter ![]() is a functional and greater than zero.
Thus by definition, the penalty cost is positive definite; hence equation (2.5)
becomes:
is a functional and greater than zero.
Thus by definition, the penalty cost is positive definite; hence equation (2.5)
becomes:
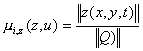 2.7
2.7
Now from (Waziri et al. 2006b), we must have that:
![]()
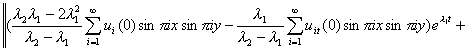
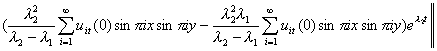 2.8
2.8
Also we have from equation (2.6) that:
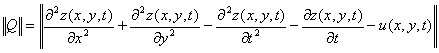 2.9
2.9
From [[4]] (Waziri et al. 2006b), we can derive:
![]()
![]() 2.10
2.10
![]()
![]()
![]()
![]() 2.11
2.11
![]()
![]()
![]()
![]() 2.12
2.12
![]()
![]()
![]()
![]() 2.13
2.13
![]()
![]()
![]()
![]() 2.14
2.14
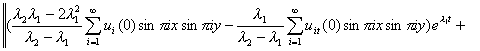
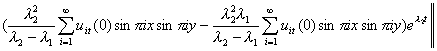
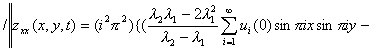
![]()
![]()
![]()
![]()
![]()
![]()
![]()
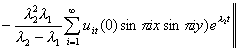 2.15
2.15
Consequently, the substitute of equation (2.9) into equation (2.7) will completely define the action of the state trajectory on the penalty. Programs codes will give us the necessary desired numerical state penalty costs at various space profiles; otherwise, heretofore refer simply as to the nth-plane or n stratum.
The numerical output for the penalized optimal state cost functional
Various penalized strata for the state functional produce the numerical outputs values in table 1 below.
Table 1. Outputs of penalty cost constants
|
s/n |
Nth-dimensional space |
Penalty cost constant |
|
1 |
n=1 |
1.12102360116197·102 |
|
2 |
n=20 |
2.09885332486185 ·104 |
|
3 |
n=30 |
1.12103290033268 ·104 |
|
4 |
n=40 |
1.12102360116197 ·105 |
|
5 |
n=50 |
3.91481868054 ·105 |
|
6 |
n=60 |
2.5982461152606 ·105 |
|
7 |
n=70 |
2.592461152606 ·105 |
|
8 |
n=80 |
2.592403454182 ·105 |
Conclusions
The general analysis from both empiricism and theoretical investigation postulate that for a good constraint satisfaction, the penalty cost constant used in moving the dynamical system constrained problem into the formulation of an unconstrained control problem, must on one hand, be sufficiently large; on the other hand, this parameter must not approach infinity as the convergence rate of most penalty methods deteriorate sharply at this instant, and many optimization techniques, as a result, are subjected to numerical instability because of the derivatives of the penalty functions or penalty functions themselves may increase without bounds in the vicinity of the minimum. This would create a paradox!
An eagle eye observation of the penalty cost constants in the above table (3.1) clearly agrees with the assertions in the paragraph before this. As the nth-stratum space increases, the penalties cost constant numerical values increase positively and maintain consistent numerical stability when the dimensional profile increases between the at all strata. This obviously shows that the convergence is achieved for the penalty cost functional. Hence, the optimal state penalty parameters give excellent convergence rates. This would give an excellent ECGM outputs that would compare favorably with the analytical manually if endurance computational processes will be sustained for quite an elaborate period of time.
References