Intelligent Search Method Based ACO Techniques for a Multistage Decision Problem EDP/LFP
Mohamed TAMALI, Mostefa RAHLI
University Of Bechar (CUB), Bechar
University of the Science and Technology of Oran (USTO) El Mnaouer, Oran, Algeria
mtamali@mail.univ-bechar.dz, rahlim@univ-usto.dz
Abstract
The implementation of a numerical library of calculation based optimization in electrical supply networks area is in the centre of the current research orientations, thus, our project in a form given is centred on the development of platform NMSS1. It's a software environment which will preserve many efforts as regards calculations of charge, smoothing curves, losses calculation and economic planning of the generated powers [23].
The operational research [17] in a hand and the industrial practice in the other, prove that the means and processes of simulation reached a level of very appreciable reliability and mathematical confidence [4, 5, 14]. It is of this expert observation that many processes make confidence to the results of simulation.
The handicaps of this approach or methodology are that it makes base its judgments and handling on simplified assumptions and constraints whose influence was deliberately neglected to be added to the cost to spend [14].
By juxtaposing the methods of simulation with artificial intelligence techniques, gathering set of numerical methods acquires an optimal reliability whose assurance can not leave doubt.
Software environment NMSS [23] can be a in the field of the rallying techniques of simulation and electric network calculation via a graphic interface. In the same software integrate an AI capability via a module expert system.
Our problem is a multistage case where are completely dependant and can't be performed separately.
For a multistage problem [21, 22], the results obtained from a credible (large size problem) calculation, makes the following question: Could choice of numerical methods set make the calculation of a complete problem using more than two treatments levels, a total error which will be the weakest one possible? It is well-known according to algorithmic policy; each treatment can be characterized by a function called mathematical complexity. This complexity is in fact a coast (a weight) overloading the algorithm getting to him a rate preferably more or less justifiable. In operational research, this subject is known under the name of CPO [14] (combinatory problem optimization).
The choice of a numerical method to use for a merged case study and calculation of the LFP/Fitting/EDP what is [7, 8, 9, 10, 18, 19, 20] (in theoretical form of a problem) compensates the final decision to adopt and a strategy of optimal production (which is a practical problem form and the final task most wanted).
Each method is imposed by:
· The algorithm complexity.
· In an application gathering all calculations, the number of uses of method compared to the total number of later issues.
· The maximum number of iterations for a given use.
· The maximum iterations count allowed for this algorithm kind.
· The limitations of the algorithm such as: applicability of a method (algorithm adapted or not to the problem); does the problem constrained or not; problem dimension or order N (N ≤ Nmax); the algorithm stability.
It's well-known that for an approached calculation method, the propagation of errors strongly conditions the need of making its adequate choice and if it can be adopted compared to others for the same area.
More is the number of the elementary operations is large more the final result misses precision and especially if the finality of the study is a responsible decision to make and a satisfaction of constraints and multiple conditions. Our study proposes an inference based solution (AI) with the use of ACO technique (Ant colony Optimization2).
Notes
1 NMSS: Network Modeling and Simulating System - software, subject of the Master Thesis presented in 1995: A software for modeling and simulating lot of tasks on electrical networks
2 Technique introduced for the first time by Marco DORIGO since 1992 [1].
Decision, LFP, EDP, Smoothing curves, Economy, Optimal study, Algorithm complexity, Numerical method, Constraint, ACO, Artificial intelligence
Introduction
NMSS is OOP based software, from where the necessity to describe all software entities in an equivalent diagrams (use of UML diagram). A set of views and dialogs perform a maximum and easy use of the platform. A main and Childs views in NMSS solution are represented with graphical interface hiding in the background mathematical libraries. The mathematical library as for it, gathers all the numerical methods applied to the supply calculation of the electrical networks. An expert engine system manages and solves the ambiguity of choice to be made to combine methods of various levels in order to pass up of all the troubles of numerical calculations good known such truncation, the propagation of error, the algorithm complexity and the choice of regulating parameters.
This study proposes like tries the determination of adaptive heuristics based on ant colony algorithm (ACO) for the qualification of the best alternative of the trio calculation levels problem in power analysis system:
· LFP (Load Flow Problem) Power flow intend calculation of vectors of nodal voltages and nodal powers, the power flows and finally of the transmission losses.
· FF (Fitting Function) Smoothing curves intend the determination of the coefficients of cost function. The major question is to see if this function is of the second or the third order, the parameters depend strongly on the data resulting from experience and the interpolation method.
· EDP (Economic Dispatch Problem) Economic planning of the generated powers; the determination of the production consigns according to a demand of energy.
These three problems are much dependant and the choice of an adequate combination of methods necessarily reducing error propagation and truncation following the use of a core of precise calculation.
The ACO as a heuristics of calculation is adapted much is advised for combinative problems and showed a remarkable effectiveness compared with the other heuristic ones and methods used to optimize the choice of a decision [1, 11, 13, 15].
In the field of energy, much of researchers used this technique [3].
The proposal for such a vision is, according to our comprehension and analyzes literature, taken into account for the first time.
Problem's Equation
To determine a mathematical formulation describing the phenomenon of the choice reserving a great attention with the following facts and assumptions:
Þ If we indicate by:
· O(x): the algorithm complexity
· Nups: Number of ulterior cessions we've use the algorithm.
· Nmiterpu: Number of maximum iterations during the ulterior cessions.
· Kmax: The maximum number of iterations limiting the algorithm.
· (mi): A special function that we adopt as filter function of the algorithm and that is based on:
Þ The following questions:
· The problem is constrained?; question that supports an answer affirming YES or invalidating NO.
· Dimension acceptable of the Nalgo algorithm compared to the problem dimension Pi [(does Algoj support Pi) ? YES, NO]
· Does Algoj algorithm be applied in this case of problem Pi
For a dimension given Np of the problem, the following table enumerates the tendencies of the possible combinations of the previous parameters.
Table 1. Picture of the tendencies of the parameters
|
Parameter |
Default Value |
Constance |
Tendency |
|
O(x) |
- |
Yes |
æ |
|
Nups |
- |
No |
ä |
|
Nmiterpu |
- |
No |
æ |
|
Kmax |
50 |
No |
essentially æ |
|
Dependency (mi) |
- |
No |
1 or 0 |
A first form of expression that the function will have is as follows:
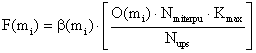 (1)
(1)
The F(mi) function defines the cost value of the path to follow if the method (mi) has just been chosen [6].
Also, a method mi can evolve in its algorithm (new variant), thing that can give him an advantage of next use. Every update, give back to the method mi additional points in more quoting it or devaluing it. This coast is dynamic.
Knowing that the calculation, for the optimization of a problem Pi given is done according to the following stages:
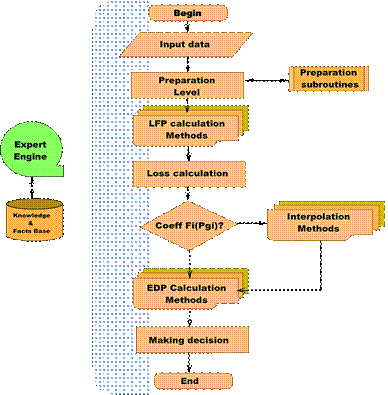
Figure 1. Summary of the calculation network (in steady state)
For a given problem Pi (a network Resi), a lot of handling ways present themselves. Every method follows an algorithm and a number of stages in order to arrive to the solution.
The following diagram illustrates the feasibility of case-study:
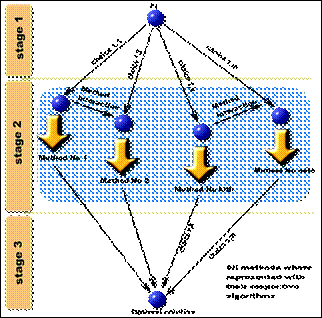
Figure 2. Problem of the choice of methods to solve a problem [14]
The choice of a path can have various forms, whereas the justification of the sensibility of the final result to the propagation of errors can't be forgotten. The intermediate stage of this topology also is composed by a complex netted structure.
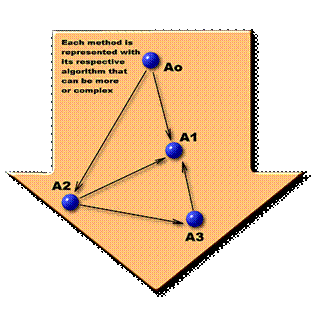
Figure 3. Internal structure of the intermediate node or stage
ACO Solution for Algorithm Choice Problem
Ant Colony Optimization by (ACO) studies the artificial systems that take the inspiration of the behaviour of true antlike colonies. It is used to perform a solution for discreet optimization problem.
Form a class of the meta-heuristic recently proposed for complex problems of optimization (NP-Complex problems and dynamic problems).
In history, the ACO techniques were born following a observation:
· In general on the behaviour of the social insects.
· In particular the colonies of ants.
In 1983 Deneubourg Jean Louis biologist, studies the behaviour of the ants. These last are able to find the shortest way from the nest to a location of food. The great remark is that they could adapt to any change of the environment. The mean of communication was at the origin of a hormone known as Pheromone.
In 1992 Dorigo Marco[1] elaborates a meta-heuristic for optimization of very wide types of problems. The first algorithm of this type has been conceived to solve the TSP Traveler's Salesman Problem.
Used Conventions
- 'Ants': Is an artificial ant that mime the behaviour of real ants.
- Ant behaviour: Use of the communication tool between the individuals.
- The pheromone: On their trip, ants let a variable quantity of pheromone on their path, that is detected by the next ants, and that determines with a big probability to access to the food localization.
- Shape of 'autocatalytic behaviour': More ants follow the path more the path becomes attractive.
Algorithm of ACO technique
1) Let all ants to the places of origin (Entry Points).
2) Initialization of the pheromone on the edges according to the weight of each (to qualify for the first time)
3) Creation of a new colony.
4) Every ant follows the proportional transition rule
While much as every ant didn't visit all nodes: Return to step 4)
5) Deposit of the local trace in relation to the best ant's finished path
6) update the new quantities of pheromone + evaporation of the global traces
7) While much as test of stop-condition not reached: Return to 3)
Figure 4. Algorithm of the ACO method
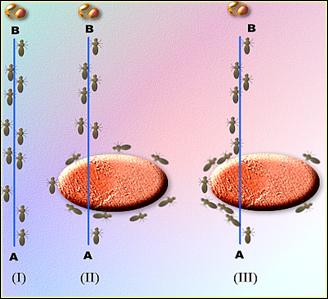
Figure 5. Observation made on real ants behavior

Figure 6. ACO method adapted to our case
This figure (Fig. 5) illustrates the fact that for a set of ants the most optimum path in order to go from the nest (A) to the food in (B) consists to follow the AB way and if by experience an obstacle is deposed on this way obliging the ants to get around it, two ways can be offer; right and left of the obstacle.
By their nature, ants, deposit an enzymatic substance so-called pheromone on their trip. This substance acts as guide for all ants who are going to follow the same path. The intensity (and its evaporation) indicates to the same creatures the information of qualification of the edge to be or not taken.
On this same illustration, the ants deposit variable quantities on their path backward from (B), localization of food and the nest (A). With this last process the other ants learn to identify the optimum path himself that makes result the fact that the least economic path will be abandoned and the whole colony will browse a minimal length leaving from (A) toward (B) or the inverse.
The ants colonies world make us notice that:
· A work of community under the base of a collective intelligence for response to the vital needs for the colony.
· The memorizing of the information which is materialized by the warehouse of a natural substance and thus its condensation or its evaporation would play the part of cooling or the loss of information in memory.
· The collective intelligence can easily be adapted to the more dynamic situations and in a perpetual change.
· The solution of the problem is independent of the number of agent moving (ants) whereas the processing time is.
· The observation of the facts lets notice that objective function to optimize by the agents (ants) equals the most possibly shortest path done.
Numerical method for optimal path search planning problem
In NMSS 4 software, the ACO technique is used in different levels and ways:
a- Adaptation of the content of knowledge base of the inference module [2, 21, 22]
b- Problem of numerical method's planning, topic of the present publication [7, 8, 9, 10].
For our case, a good adaptation of the choice to recommend a trio of combined numerical methods answers exigencies holding more to the fact that these methods are more in stable, algorithmic complexity with P type and realizable [14].
The figure 6 illustrates this principle.
The good solution witch can be obtained according to our case-study requires the search of a most optimal path among others whose cost or time complexity is the favourable.
The problem of this survey is to move from an entry to an exit point trough a multiple stage that makes the adaptation of ACO algorithm to be in agreement with the multistage form and data [5] with satisfaction with problem's conditions and constraints:
· All ants will have the same departure (be(t0) = m; be is the number of ants to the e entry of the representative graph and t0 at the instant 0 of the beginning).
· Every kith ant passes only ones by stage (LFP, Fitting or EDP)
· The optimal value is evaluated by the cost of the list distance covered between the nodes visited by each ant from e to s (s being the exit)
· In every node, only authorized paths are offered.
On this context, the minimum value of number of ants cannot be lower to the number of nodes of problems like graph.
Every edge is quoted with a weight measuring the importance of the algorithm being upstream.
Adaptation of the ACO algorithm in an ACSA[2] problem
(Path search problem)
1) Let all ants to the e entry point of a multistage graph.
2) Initialization of the pheromones on edges according to the weight of each relative algorithm.
3) Formation of 'tabu-list' of every ant (first value for the whole colony is {e})
4) Every ant move to next point in the next stage according to the proportional transition rule
5) Update the local trace of pheromone and calculate the best edge cost obtained.
6) Addition of the new pheromones +evaporation in global traces.
7) If Stop-test non reached: Return in 3).
Figure 7. An Adapted ACO Algorithm
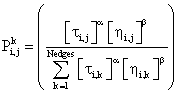 (2)
(2)
Where ti,j is the trace of pheromone on edge (i,j), hi,j is the visibility and a, b (wich are the real constants) are respectively the importance of pheromone and the distance between nodes i and j.
Implementation of the algorithm
The methodology shown above has been implemented and validated under Visual Basic 2005 environment and tested on a Centrino microprocessor of Intel based machine with 2.8 GHz.
The results obtained for a 5 buses standard IEEE electric network that data are illustrated in the following figures and tables:
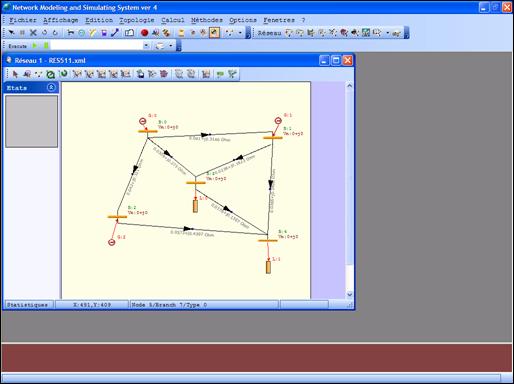
Figure 8. Snapshot of NMSS 4 Main window and client document opened
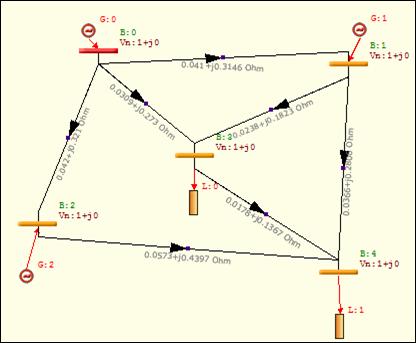
Figure 9. Diagram of the network executed on NMSS 4
Table 2. Data of network (Experience of smoothing curves)
|
Pgi |
Fi(Pgi) |
|
10 |
4730.36 |
|
30 |
9676.26 |
|
50 |
15522.82 |
Table 3. Lines data of the standard network IEEE 5 buses
|
p-q |
Zser |
Ysh |
|
1-2 |
0.0410+j0.3146 |
j0.07 |
|
1-3 |
0.042+j0.321 |
j0.0715 |
|
1-4 |
0.0309+j0.273 |
j0.0528 |
|
2-4 |
0.0238+j0.1823 |
j0.0405 |
|
2-5 |
0.0366+j0.2806 |
j0.0624 |
|
3-5 |
0.0573+j0.4397 |
j0.0978 |
|
4-5 |
0.0178+j0.1367 |
j0.0300 |
Table 4. Table of planning
|
Node |
Type |
P (pu) |
Q (pu) |
V (pu) |
d (°) |
|
1 |
slack |
- |
- |
1.0 |
0 |
|
2 |
Generator |
0.931 |
- |
1.0+j0.0 |
- |
|
3 |
Generator |
0.900 |
- |
1.0+j0.0 |
- |
|
4 |
Load |
-2.202 |
-1.031 |
- |
- |
|
5 |
Load |
-0.911 |
-0.212 |
- |
- |
Table 5. Constrains of the active powers and cost functions
|
PG1min£ PG1£ PG1max |
|
PG2min £ PG2 £PG2max |
|
PG3min £ PG3 £ PG3max |
|
F1(PG1)=3409.235+138.0899*PG1+0.4079592*PG12 |
|
F2(PG2)=3409.235+138.0899*PG2+0.4079592*PG22 |
|
- to be calculated according to the data of the figure 2 |
Results gotten by NMSS 4 (Normal calculus)
Table 6. LFP stage
|
Gauss-Seidel |
Relaxation |
|
1+j0 |
1+j0 |
|
1.009933-j.076137 |
1+j0 |
|
1.021812+j.16699 |
1+j0 |
|
923658+j.100462 |
1.037647-j.06723 |
|
938855+j.073528 |
1.069389-j.137139 |
Table 7. Fitting function stage
|
Coefficients |
The least squares method |
Interpolation Lagrange polynomials |
|
A |
2595.15750000002 |
2595;1575 |
|
B |
202.26199999998 |
202;262 |
|
C |
1.1258250000004 |
1.125825 |
Table 8. EDP stage
|
Pgi |
Simplex Method |
Lagrangian Method |
|
1 |
145.0 |
69.3655 |
|
2 |
111.3 |
105.7950 |
|
3 |
55.0 |
136.1395 |
ACO Search results
For every stage we define the following terms:
Table 9. Methods used
|
Stage |
available Method (implemented |
|
|
1 |
(GSE):Gauss-Seidel |
(REL):Relaxation method |
|
2 |
(LSQ):Least square |
(PLA):Lagrange Polynomials |
|
3 |
(SMP):Simplex Method |
(LAG):Lagrangian Method |
The combinative [6, 14] character of problem gives us the following choices:
(GS)/(LSQ)/(SMP); (GS)/(PLA)/(SMP),
This arborescence becomes more and more complex while the number of method grows. Treatment becomes very hard and so difficult is the making of any choice.
The presented algorithm qualifies a liberty in the diversity of the possible choices. This adaptive tendency is in the centre of the techniques of inference engine implemented in NMSS 4.
Other methods can be proposed to solve the same problem like Dijkstra method, the simulated annealing method, the TABU-SEARCH, Genetic Algorithms method or all other variant of ACO path search techniques.
We must notify that all stages in calculation process are dependant, EDP stage needs transmission Loss value which is gotten in LFP stage, EDP also can't be performed without coefficients of cost-functions of all generator buses.
The diagram that simulate the process of choice is shown in the figure below (Fig 8)
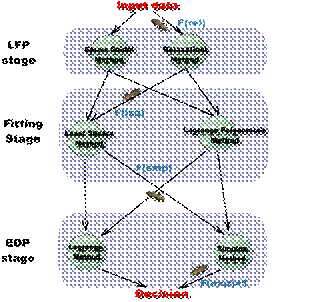
Figure 8. Choice process with ACO method
Where F( ) the objective function evaluated for this transition equivalent to distance of the edge in the TSP problem.
If all edges are denoted with the same weight F(..), the method's choice can be anything but while weights are different, the ACO transition formula must give the optimum move to do according to method parameters (such as algorithm complexity, maximum number of iterations an so on).
The following hypothesis shows the parameters that can be used to perform a decision.
Table 10. Objective function variable value
|
Variable |
Default Value |
|
n |
8 |
|
O(x) |
GSE: n3 = 512 REL: n2 = 64 LSQ: n2 = 64 PLA: n2 = 64 SMP: n! = 40320 LAG: n2 =64 |
|
Nups |
1 |
|
Nmiterpu |
1 |
|
Kmax |
50 |
|
Dependency (mi) |
1 |
The results are reported in a table below.
Table 11. Results of the optimization
|
With N=8 cities a=0.9 b=0.5 r=0.2 Nant = 10 Availability : 2x4x4x2 paths to compare The optimum choice gotten gives : e-REL-PLA-LAG-s |
What means that planning a combined treatment with relaxation method for LFP, a Lagrange polynomials interpolation method for fitting function and Lagrangian Method for EDP should reduce all calculation mistakes and then gives an additional help to make a good decision.
Conclusion
The propagation of the errors and its influence on the final result are major. Thing that lets to judge that the choice of a good combination of numeric methods imposes the decision attended to make a planning of tasks for dispatching consigns according to a total demand of energy.
NMSS 4, intend like tool of validation and help to the decision conceived around a practiced system. The future waited versions of NMSS 4, will reveal for its account others faculties and abilities.
This strategy gives clearly the proofs that the ACO techniques add-in for an expert system is mainly recommended in addition to other intelligent techniques.
The inference methodology based natural-like behaviour (ant agent behaviour).
The pheromone (agent contribution) levels along graph's edges and its distance (real data with a direct influence in the objective function) can have a big importance in a path choice.
Other complexities must be treated in our future works like time complexity or a merged form that combine the algorithmic and time complexities.
Outline for future work
It's also an open-end; a lot of work must be performed using ACO techniques and algorithms. A development of an inference engine requires a great attention. The ACO meta-heuristic like, can be expanded to manage a decision that can be done with this mathematical tool.
The optimal values of control parameters in ACO algorithms (a, b, r) need to be treated in their respective range values. For this issue the genetic algorithms can be proposed such a smoother.
References
[1] Dorigo M., Optimization, learning and natural algorithms, Ph.D. Thesis, Dip Elettronica e Informazione, Politecnico di Milano, Italy, 1992.
[2] Kazarlis S., Petridis V., Fragkou P., Solving University Timetabling Problems Using Advanced Genetic Algorithms, 5th International Conference on Technology and Automation, October 15-16, 2005, Thessaloniki, Greece, Proceedings of the ICTA05, p. 131-136, http://icta05.teithe.gr/.
[3] Sum-im T., Ongsakul W., Ant colony search algorithm for unit commitment, IEEE International Conference on Industrial Technology, Vol. 1, 10-12 Dec. 2003, p. 72-77, 2003.
[4] Dorigo M., Di Caro G., Gambardella L. M., Ant Algorithms for Discrete Optimization, Artificial Life, 5, p. 137-172, 1999.
[5] Birattari M., Di Caro G., Dorigo M., Toward the formal foundation of Ant Programming, Proceedings of Ant Algorithms: Third International Workshop, ANTS 2002, Brussels, Belgium, September 12-14, 2002, in Lecture Notes in Computer Science, Vol. 2463, p. 188-201, 2002.
[6] Semet Y., Jamont Y., Biojout R., Lutton E., Collet P., Artificial Ant Colonies and E-Learning: An Optimisation of Pedagogical Paths, HCII'03: 10th International Conference on Human-Computer Interaction, June 22-27, 2003, Crete, Greece, then Human-Computer Interaction: Theory and Practice (part 2), Vol. 2, Lawrence Erlbaum Associates, 2003.
[7] Sum-im T.; "Economic Dispatch by Ant Colony Search Algorithm"; Proceedings of the 2004 lEEE Conference on Cybernetics and intelligent Systems Singapore, 1-3 December, 2004.
[8] Bakirtzis A., Petridis V., Kazarlis S.; Genetic algorithm solution to the economic dispatch Problem; IEE Proc.-Gener. Transm. Distrib., Vol. 141, No. 4, July 1994.
[9] YaICinoz T., Short M.J.; Large-scale economic dispatch using an improved Hopfield neural network; IEE Proc.-Gener. Transm. Distrib., Vol. 144, No. 2, March 1997.
[10] Yalcinoz T., Altun H., & Hasan U.; Constrained Economic Dispatch With Prohibited Operating Zones : A Hop field Neural Network Approach; 1 0, Mediterranean Electrotechnical Conference, MEleCon 2000, Vol. I1 0-7803-6290-X/02000 IEEE.
[11] Li Y. and Xu Z.; An Ant Colony Optimization Heuristic for Solving Maximum Independent Set Problems; Proceedings of the Fifth International Conference on Computational Intelligence and Multimedia Applications (ICCIMA03) 0-7695-1957-1, 2003 IEEE.
[12] Blum C., Dorigo M.; "The Hyper-Cube Framework for Ant Colony Optimization"; IEEE transaction on system, man, and cybernetics-Part B: CYBERNETICS, VOL. 34, No. 2, APRIL 2004.
[13] Subrata R., Zomaya A.Y.; A Comparison of Three Artificial Life Techniques for Reporting Cell Planning in Mobile Computing; IEEE Transactions on parallel and distributed systems", VOL. 14, NO. 2, February 2003.
[14] Shiba T., Tsuchiya T., Kikuno T.; Using Artificial Life Techniques to Generate Test Cases for Combinatorial Testing, COMSPAC'2004; Proceeding of 28th Annual International, p. 72-77 VOL. 1, September 2004.
[15] Ritchie G., Levine J.; A hybrid ant algorithm for scheduling independent jobs in heterogeneous computing environments;, American Association for Artificial Intelligence, Proceedings of the 23rd Workshop of the UK Planning and Scheduling Special Interest Group (PLANSIG 2004), 2004, (www.aaai.org).
[16] Dorigo M.and Di Caro G.; Ant Algorithms for Discrete Optimization; Arti cial Life, 5(2):137-172, 1999.
[17] Tarasewich P., Swarm Intelligence: Power in Numbers; Communications of the ACM, August 2002, 45(8), p. 62-67
[18] Durairaj S., Kannan P.S.; Multi-Objective VAR Dispatch Using Particle Swarm Optimization; Electric Power Systems; International Journal of Emerging Electric Power Systems Volume 4, Issue 1; 2005; Article 1082
[19] Sheble G.B.; Real-time economic dispatch and reserve allocation using merit order loading and linear programming rules; IEEE Transactions on Power Systems, Vol. 4, No. 4, October 1989.
[20] Liu D., Cai Y.; Taguchi Method for Solving the Economic Dispatch Problem with Nonsmooth Cost Functions; IEEE transaction on power system, VOL. 20, NO. 4, November 2005.
[21] Yu W., Tie-Jun W.; Dynamic Window Search of Ant Colony Optimization for Complex Multi-stage Decision Problems; 0-7803-7952-7/03/Q; 2003; lEEE.
[22] Konar A.; Artificial Intelligence and Soft Computing; CRC Press, 2000; Pg 483-486.
[23] Tamali M.; Conception d'un logiciel de modélisation et simulation des réseaux électriques NMSS; Master thesis equivalent diploma; presented in 1995.
Short CVs
 Mostefa Rahli was born on October 24, 1949 in Mocta-Douz, Mascara, Algeria. He received his B.S. degree in electrical engineering from the
Electrical Engineering Institute in The University of Sciences and Technology
of Oran (USTO) Algeria in 1979, the M.S. degree from the Electrical Engineering
Institute of The University of Sciences and Technology of Oran (USTO) in 1985,
and the Ph.D. degree from the Electrical Engineering Institute of The
University of Sciences and Technology of Oran (USTO) in January 1996. From 1987
to 1991, he was a visiting professor at the University of Liege
(Montefiores Electrical Institute) Liege (Belgium) where he
worked on Power Systems Analysis under Professors Pol Pirotte and Jean Louis
Lilien.
Mostefa Rahli was born on October 24, 1949 in Mocta-Douz, Mascara, Algeria. He received his B.S. degree in electrical engineering from the
Electrical Engineering Institute in The University of Sciences and Technology
of Oran (USTO) Algeria in 1979, the M.S. degree from the Electrical Engineering
Institute of The University of Sciences and Technology of Oran (USTO) in 1985,
and the Ph.D. degree from the Electrical Engineering Institute of The
University of Sciences and Technology of Oran (USTO) in January 1996. From 1987
to 1991, he was a visiting professor at the University of Liege
(Montefiores Electrical Institute) Liege (Belgium) where he
worked on Power Systems Analysis under Professors Pol Pirotte and Jean Louis
Lilien.
He is currently Professor of electrical engineering at The University of Sciences and Technology of Oran (USTO), Oran, Algeria. His research interests include operations, planning and economics of electric energy systems, as well as optimization theory and its applications. He is actually Member IEEE.
Address:
Electrical Department, Faculty of Electrical Engineering, USTO; BP 1505, Oran El Mnaouer, Oran, Algeria.
Tel/Fax: 213 41 42 55 09
E-mail: rahlim@yahoo.fr, rahlim@univ-usto.dz

Mohamed Tamali was born on august 20, 1960 in Bechar, Algeria. He received
his B.S. degree in electrical engineering from the Electrical Engineering
Institute of The University of Sciences and Technology of Oran (USTO) in 1986,
the M.S. degree in Energetically Physics from the Mechanics Institute of
The Bechar University Center (CUB) in 1995. He actually works, From
October 1986, at the same university where he dispenses a credit related
to Simulation and Optimization of Electrical Network. Another credit like
Optimization Theory, Simulation and Applications in the Internet Network are teaches
to students of informatics speciality. He was since 1992, the Internet Network
Administrator for what is received his AUF Certificate (Cession organised by
CERIST Algeria and EEC). In 2000, he was designed at the
POP Bechar Responsible at CERIST Institution.
His research interests include operational research, Algorithmic Methodology
applied to calculation of Electrical planning and economics of electric energy
systems, as well as optimization theory and its applications. The Optimization
heuristics are in the centre of his interest.
Address:
Electrical Institute, CUB; BP 1407, Bechar Route de Kenadsa, Bechar, Algeria.
Tel: +(213)49815581, Fax: +(213)49819024
Email: mtamali@mail.univ-bechar.dz, tamalim@hotmail.com.