Economic Load Dispatch with Security Constraints of the Algerian Power System using Successive Linear Programming Method
Samir SAYAH, Khaled ZEHAR
Department of Electrical Engineering, University of Ferhat Abbas, Setif, ALGERIA
samir_pg04@yahoo.fr, khaledzehar@yahoo.fr
Abstract
This paper presents a solution of the economic load dispatch (ELD) problem with security constraints of power systems, using an iterative technique based on the linear programming method, called “Successive Linear Programming” (SLP). The objective is to minimize the nonlinear function which is the total fuel cost of thermal generating units, while taking into account the security constraints (power generations, voltages and line flows). The proposed approach has been implemented on the Algerian 59-bus system. Simulation results obtained from the proposed method confirm the advantage of computation rapidity and solution accuracy. The comparison results prove the capability of the proposed method in real-time implementation for the economic load dispatch problem.
Keywords
Economic load dispatch, Security constraints, Power system optimization, Algerian power system, Successive linear programming
Introduction
Economic load dispatch (ELD) is an important function in power system planning and operation. ELD solutions are found by solving the conventional load flow equations while at the same time minimizing fuel costs. The resulting optimization problem has nonlinear constraints from the load flow nodal equations and simple bound constraints on the variables from the load bus voltage magnitudes.
In 1962, Carpentier [1] introduced a generalized nonlinear programming formulation of the economic dispatch problem, including voltage and other operating constraints. This formulation was later named the Optimal Power Flow (OPF) problem. In 1968, Dommel and Tinney [2] introduced a reduced gradient steepest descent algorithm to solve the optimization problem. This algorithm has two drawbacks: slow convergence with the steepest descent direction, and ill conditioning resulting from the penalty functions associated with the inequality constraints.
Today any problem that involves the determination of the instantaneous optimal steady state of an electric power system is an OPF problem. Traditionally, different solution approaches have been developed to solve the different classes of the OPF problem. These methods are nonlinear programming techniques with very high accuracy, but their execution time is very long and they can not be applied to real-time power system operations.
Since the introduction of the sequential or successive programming techniques, it has become widely accepted that successive linear programming (SLP) algorithms can be effectively used to solve the ELD problem [3]. In SLP, the original problem is solved by successively approximating the original problem using Taylor series expansion at the current operating point and then moving in an optimal direction until the solution converges.
In this paper, a method based on an efficient successive linear programming technique is presented and tested on the Algerian 59-bus power system. Simulation results obtained from the proposed method confirm the advantage of computation rapidity and solution accuracy. These results show great promise for on-line application of the proposed approach for the ELD problem.
ELD problem formulation
The ELD problem is considered as a general minimization problem with constraints, and can be written in the following form:
|
Minimize f(x) |
(1) |
|
Subject to: g(x) = 0 |
(2) |
|
h(x) ≤ 0 |
(3) |
f(x) is the objective function, g(x) and h(x) are respectively the set of equality and inequality constraints. x is the vector of control and state variables. The control variables are generator active and reactive power outputs, bus voltages, shunt capacitors/reactors and transformers tap-setting. The state variables are voltage and angle of load buses.
Objective function
The objective function for the ELD reflects the costs associated with generating power in the system. The quadratic cost model is used. The objective function for the entire power system can then be written as the sum of the quadratic cost model for each generator:
![]() [$/h] (4)
[$/h] (4)
where ng is the number of thermal units, Pgi is the active power generation at unit i and ai, bi and ci are the cost coefficients of the ith generator.
Equality constraints
The equality constraints g(x) of the ELD problem are represented by the power balance constraint, where the total power generation must cover the total power demand and the power loss. This implies solving the load flow problem, which has equality constraints on active and reactive power at each bus as follows [4]:
 (5)
(5)
where: i=1,2,..., n and θij = θi - θj; Pi, Qi: injected active and reactive power at bus I; Pdi, Qdi: active and reactive power demand at bus i; Vi, θi: bus voltage magnitude and angle at bus i; Gij, Bij: conductance and susceptance of the (i,j) element in the admittance matrix.
Inequality constraints
The inequality constraints h(x) reflect the limits on physical devices in the power system as well as the limits created to ensure system security:
· Upper and lower bounds on the active and reactive generations:
![]() (6)
(6)
· Upper and lower bounds on the tap ratio (t) and phase shifting (α) of variable transformers:
![]() (7)
(7)
· Upper limit on the active power flow (Pij) of line i-j:
![]() (8)
(8)
where [5]:
![]() (9)
(9)
· Upper and lower bounds on the bus voltage magnitude:
![]() (10)
(10)
SLP Based Method for Solving the ELD Problem
Because of the nonlinear nature of the electric power system, ELD problems are nonlinear programming problems. So, its resolution requires a nonlinear optimization technique like Newton's method [6]. Another widely used method is the linear programming (LP) technique [7, 8, 9]. The SLP method linearizes the objective function and constraints around the current operating point to set up and solve the problem using the LP technique. The control vector is updated and a new state is computed that is better than the previous one. The above procedure is successively repeated until the desired objective is achieved [10].
The ELD problem can be restated as [10]:
|
Minimize · f(x,u) Subject to: · gi(x,u) = 0, i=1, ..., n · hj(x,u) ≤ 0, j=1,...,m · xmin ≤ x ≤ xmax · umin ≤ u ≤ umax |
(11) |
Where:
· x and u are respectively the state and the control vector.
· xmin and xmax are respectively the lower and the upper limit on the state vector.
· umin and umax are respectively the lower and the upper limit on the control vector.
The problem (11) is linearized around the current operating point (xo, uo), and formulated as an LP problem:
|
Minimize ·
Subject to: ·
·
|
(12) |
Where:
·
![]() and
and ![]() are the jacobean sub matrix.
are the jacobean sub matrix.
This linearization is only accurate for a small variation (±σ) of the increments Δx and Δu, so:
-σ ≤ Δx ≤ σ, -σ ≤ Δu ≤ σ (13)
However, in any case, the original bounds (xmin, umin) and (xmax, umax) should not be violated by the increments. Hence, we have the following new bounds on Δx and Δu [11]:
|
|
(14) |
The linearized problem given by (12) and (14) is an LP problem.
In order to reduce the size of the LP problem, we can solve the linearized equality constraints (decoupled load flow equations), and express the relation of Δx in term of Δu. The expression of Δx is then substituted in inequality constraints. Hence, the problem is expressed in term of control vector Δu only. The solution of the LP problem gives the increment control vector Δu, and added to the initial control uo provides a new updated vector u given by:
u = uo + Δu (15)
A new operating point (x , u) is calculated using the fast decoupled load flow algorithm [12]. The procedure is successively repeated until the desired objective achieved.
Development of the SLP Based Model
Objective function
The objective function is the cost function linearized around the current operating point (Pg(k), V(k), θ(k)), given by:
Δf(x,u) = [Jf(k)][ΔPg] (16)
where:
· [Jf(k)] is the jacobean line vector of f(x).
· [ΔPg] is the increment column vector of active power generation.
The jacobean elements of [Jf(k)] are given by:
![]() (17)
(17)
Equality constraints
The equality constraints are based on the decoupled load flow equations [12]. The linearization around the control vector [Pg(k)] gives:
![]() (18)
(18)
where:
· [Pd] is the active power demand vector.
· [P(k)] is the net injection power vector.
· [Δθ] is the increment column vector of bus voltage angle.
· [B'] is the susceptance matrix.
From (18) we can write:
![]() (19)
(19)
Inequality constraints
The inequality constraints reflect the limits on physical devices in the power system, to ensure system security.
· Limits of active power generation and voltage magnitude:
![]() (20)
(20)
It should be noted that the constraints on the reactive power at each generator are not included in the problem as stated above. These constraints will be taken care of by treating a generator bus at a Q limit as a load bus, in the load flow algorithm.
· Limits of the line and transformer active power flow:
![]() (21)
(21)
where:
· [PB] is the vector of line active power.
· [PB(k)] is the vector of line active power flow at operating point k.
[Jhθ] and [Jhν] are the jacobean sub matrix.
Considering the physical weak coupling between P and V, and between Q and θ [12], we can approximate the equation (21) by:
![]() (22)
(22)
The jacobean sub matrix [Jhθ] is given by:
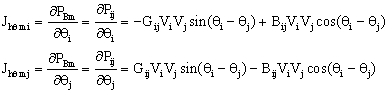 (23)
(23)
The equality constraints can be eliminated by replacing (19) in (22):
![]() (24)
(24)
The equation (24) is expressed in term of the increment [ΔPg] only. The inequality constraints can be written in the following form:
![]() (25)
(25)
![]() (26)
(26)
Summary of the SLP Model
In summary, the SLP based model of ELD problem can be written in the following form:
|
Minimize ·
Subject to: ·
·
·
|
(27) |
In this formulation, the variables are the elements of the control vector ΔPg.
The SLP ELD Algorithm
The basic steps required in the SLP ELD algorithm are summarized as follows [10]:
Step 1. Solve the load flow problem to obtain a feasible solution that satisfies the power balance equality constraint.
Step 2. Linearize the objective function and inequality constraints around the load flow solution and formulate the LP problem (27).
Step 3. Solve the LP problem and obtain optimal incremental control variables ΔPg.
Step 4. Update the control variables: Pg(k+1) = Pg(k) + ΔPg.
Step 5. Obtain the load flow solution with updated control variables.
Step 6. If ΔPg in step 3 are bellow user defined tolerance the solution converges. Otherwise, go to step 2.
Application Example
The SLP ELD algorithm (SLP_ELD) is coded in the MATLAB environment, and run using an AMD Athlon XP 1.8 GHz processor, with 256 MO of RAM. The test is performed on the Algerian 59-bus system [13, 14]. This network consists of 59 buses, 10 generators, 36 loads and 83 branches. Some line flow limits are modified to show the effects of these limits on the results.
Table 1 shows the technical and economic parameters of the ten generators (it is noting that the generator no. 5 at bus no. 13 is not in service).
In first case, the security constraints considered are the voltage magnitudes with active and reactive power of generators. In a second case, the security constraints consisting in the line and transformer active power flow are included.
Table 1. Technical and economic parameters of the Algerian 59-bus system
|
Bus |
Gen. |
Vmin (pu) |
Vmax (pu) |
Pgmin (MW) |
Pgmax (MW) |
Qgmin (Mvar) |
Qgmax (Mvar) |
a ($/h) |
b ($/MWh) |
c ($/MW2h) |
|
1 |
G.1 |
0.9 |
1.1 |
8 |
72 |
-10 |
15 |
0 |
1.50 |
0.0085 |
|
2 |
G.2 |
0.9 |
1.1 |
10 |
70 |
-35 |
45 |
0 |
2.50 |
0.0170 |
|
3 |
G.3 |
0.9 |
1.1 |
30 |
510 |
-35 |
55 |
0 |
1.50 |
0.0085 |
|
4 |
G4 |
0.9 |
1.1 |
20 |
400 |
-60 |
90 |
0 |
1.50 |
0.0085 |
|
13 |
G.5 |
0.9 |
1.1 |
15 |
150 |
-35 |
48 |
0 |
2.50 |
0.0170 |
|
27 |
G.6 |
0.9 |
1.1 |
10 |
100 |
-20 |
35 |
0 |
2.50 |
0.0170 |
|
37 |
G.7 |
0.9 |
1.1 |
10 |
100 |
-20 |
35 |
0 |
2.00 |
0.0030 |
|
41 |
G.8 |
0.9 |
1.1 |
15 |
140 |
-35 |
45 |
0 |
2.00 |
0.0030 |
|
42 |
G.9 |
0.9 |
1.1 |
18 |
175 |
-35 |
55 |
0 |
2.00 |
0.0030 |
|
53 |
G.10 |
0.9 |
1.1 |
30 |
450 |
-100 |
160 |
0 |
1.50 |
0.0085 |
Case 1
The results are shown on Table 2. The optimum active powers and reactive powers are in their secure limits. From Fig. 1 and 2, it can be observed that the security constraints are satisfied for voltage magnitudes. No load bus is under its lower limit of 0.90 pu. The voltage angles are between a minimum value of -13.02° and a maximum value of 7.73°.
Table 2. Results of SLP_ELD without line flow constraints for the Algerian 59-bus system
|
Generator |
Pg (MW) |
Qg (Mvar) |
|
G.1 |
37.801 |
3.859 |
|
G.2 |
38.544 |
9.779 |
|
G.3 |
134.890 |
-3.363 |
|
G4 |
127.160 |
90.000 |
|
G.5 |
0.000 |
-35.000 |
|
G.6 |
27.332 |
28.255 |
|
G.7 |
34.290 |
21.175 |
|
G.8 |
49.850 |
45.000 |
|
G.9 |
117.080 |
21.168 |
|
G.10 |
137.230 |
89.440 |
|
Total power generation |
704.177 |
270.313 |
|
Total power demand |
684.10 |
311.60 |
|
Total loss |
20.077 |
-41.287 |
|
Cost ($/h) |
1777.13 |
|
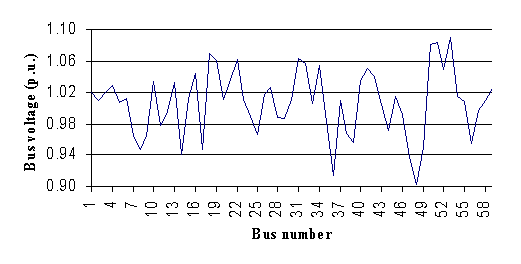
Fig. 1. Voltage profile of the Algerian 59-bus system after optimization (case 1)
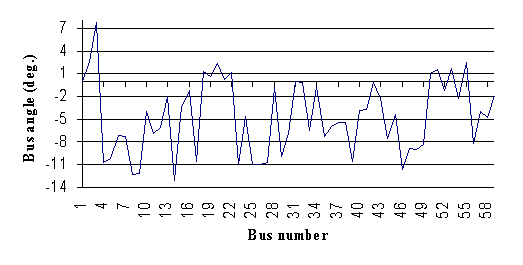
Fig. 2. Voltage angle of the Algerian 59-bus system after optimization (case 1)
The evolution of the fuel cost function during the optimization process is shown in Fig. 3. It can be observed that the production cost starts from the initial value of 1943.70 $/h, and the change of the operating points is performed on optimal steps, adjusted successively by the LP algorithm. The optimal operating point has been obtained after 4.30 seconds and 30 iterations with the optimal cost of 1777.13 $/h.
The results of the proposed approach were compared to those reported using genetic algorithm (GA) [13] and ant colony optimization method (ACO) [14]. The comparison results are given in Table 3. From this table, it can be seen that SLP_ELD method give better results than other methods and the saving in fuel cost is about 337873.20 $/year to 1401337.20 $/year. This demonstrates the potential and effectiveness of the proposed method to solve the nonlinear optimization problems.
It is important to note that the total active losses obtained with SLP_ELD are minimum compared with those obtained with other methods. The reduction of losses is about 32.12 % to 49.80%.
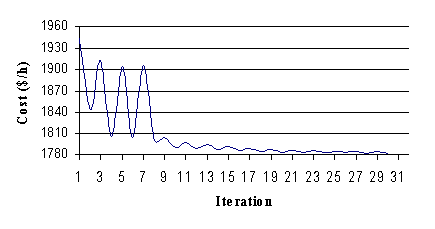
Fig. 3. Evolution of fuel cost of the Algerian 59-bus system
Table 3. Comparison results
|
|
GA [13] |
ACO [14] |
SLP_ELD |
|
Pg1 (MW) |
70.573 |
64.010 |
37.801 |
|
Pg2 (MW) |
56.574 |
22.750 |
38.544 |
|
Pg3 (MW) |
89.275 |
82.370 |
134.890 |
|
Pg4 (MW) |
78.224 |
46.210 |
127.160 |
|
Pg5 (MW) |
0.000 |
0.000 |
0.000 |
|
Pg6 (MW) |
57.930 |
47.050 |
27.332 |
|
Pg7 (MW) |
39.550 |
65.560 |
34.290 |
|
Pg8 (MW) |
46.400 |
39.550 |
49.850 |
|
Pg9 (MW) |
63.580 |
154.230 |
117.080 |
|
Pg10 (MW) |
211.580 |
202.360 |
137.230 |
|
Cost ($/h) |
1937.10 |
1815.70 |
1777.13 |
|
Loss (MW) |
29.58 |
39.98 |
20.077 |
|
Execution time (sec.) |
3.10 |
25.00 |
4.26 |
From the comparison results, it is clear that the SLP_ELD gives global optimum with less computation time than ACO method, and a comparable time to GA method.
Case 2
In this case, the line active power flow constraints are included in the inequality constraints. The active power flow of the lines should not be exceed the limit of 100 MW. The simulation results are shown in Table 4. It can be observed that the fact to limit the line flow of transmission lines, the production cost has increased from 1777.13 $/h to 1788.06 $/h (+0.61%). The line flow profile is shown in Fig. 4. From this figure, it is clear that there is no violation of the security constraints for line flows. It is also seen that the power flow of lines number 15 and 71 are enforced at their maximum limits (100 MW). The enforced line flows are shown in Table 5. This clearly indicates the trade-off between production cost and line flow constraints. The convergence has been achieved after 3.12 seconds with 12 iterations.
Table 4. Results of SLP_ELD with line flow constraints for the Algerian 59-bus system (case 2)
|
Generator |
Pg (MW) |
Qg (Mvar) |
|
G.1 |
27.421 |
3.673 |
|
G.2 |
39.328 |
9.593 |
|
G.3 |
133.770 |
-3.265 |
|
G.4 |
131.130 |
90.000 |
|
G.5 |
0.000 |
-35.000 |
|
G.6 |
26.969 |
27.030 |
|
G.7 |
33.410 |
22.002 |
|
G.8 |
70.063 |
45.000 |
|
G.9 |
100.010 |
20.401 |
|
G.10 |
142.280 |
88.272 |
|
Total power generation |
704.381 |
267.706 |
|
Total power demand |
684.10 |
311.60 |
|
Total loss |
20.278 |
-43.894 |
|
Cost ($/h) |
1788.06 |
|
Table 5. Enforced line flows (case 2)
|
Line number |
Line flow without constraints (MW) |
Line flow with constraints (MW) |
Line flow limit (MW) |
|
15 |
100.73 |
100.00 |
100.00 |
|
71 |
117.13 |
100.00 |
100.00 |
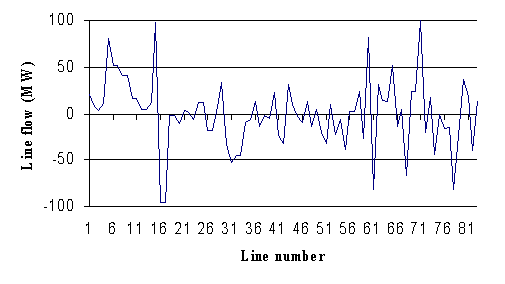
Fig. 3. Line flow profile of the Algerian 59-bus system
Conclusion
In this paper, successive linear programming algorithm was applied to solve the economic load dispatch problem with security constraints. The approach was tested on the Algerian 59-bus 10-generator system. The SLP_ELD results were compared with those obtained from genetic algorithm method and ant colony optimization approach to validate the effectiveness of the proposed algorithm. The main security constraints considered are the generated active and reactive powers as well as the voltage magnitudes. The active power flow limit of transmission lines were incorporated later in the security constraints of the problem, and the overloaded lines were observed. Simulation results show that the consideration of line flow constraints can enforce some line flows at their maximum limits, leading to an increase of the total production cost.
Considering the cases and comparative study presented in this paper, SLP_ELD algorithm appears to be very efficient in particular for its fast convergence to the global optimum and its interesting financial profit. This method is highly appropriate for on-line applications in power systems.
References
[1] Carpentir J., Contribution à l’étude du dispatching économique, Bulletin de la Société Française des Electriciens, vol. 3, August 1962.
[2] Dommel H. W., Tinney W. F., Optimal power flow solutions, IEEE Trans. on Power Apparatus and Systems, vol. PAS-87, October 1968, p. 1866-1876.
[3] Torres G. L., Quintana V. H., Optimal power flow via interior point methods: an educational tool in Matlab, in Proceeding of Canadian Conference on Electrical and Computer Engineering, vol. 2, May 26-29 1996, p. 996-999.
[4] Stevenson W. D., Elements of power system analysis, McGraw Hill International editions, 1982.
[5] Wood A. J., Wollenberg B. F., Power generation operation and control, John Wiley & Sons, 1984.
[6] Weber J. D., Implementation of a Newton-based optimal power flow into a power system simulation environment, Master thesis, University of Illinois at Urbana-Champaign, 1997.
[7] Alsac O., Bright J., Prais M., Sttot B., Further developments in LP-based optimal power flow, IEEE Trans. on Power Systems, 5(3), August 1990, p. 697-711.
[8] Mukherjee S. K., Recio A., Doulegeris C., Optimal power flow by linear programming based optimization, in Proceedings of Southeastcon, IEEE, 2, April 12-15, 1992, p. 527-529.
[9] Sttot B., Marinho J. L., Linear programming for power system network security applications, IEEE Trans. On Power Systems, vol. PAS-98, no. 3, May/June 1979, p. 837-848.
[10] Venkatesh B., Sadasivam G., Fuzzy logic based successive LP method for reactive power optimization, Electric Machines and Power Systems, Taylor & Francis, Inc., vol. 27, 1999, p. 1141-1160.
[11] Palacios-Gomez F., Nonlinear optimization by successive linear programming, Management Science, vol. 28, no. 10, October 1982, USA, p. 1106-1112.
[12] Kundur P., Power system stability and control, McGraw Hill International editions, 1994.
[13] Bouktir T., Slimani L., Optimal power flow of the Algerian network using an ant colony optimization method, Leonardo Journal of Sciences, Issue 6, July-December 2005, p. 43-57.
[14] Bouktir T., Slimani L., Optimal power flow of the Algerian network using genetic algorithms, WSEAS Transactions on Circuit and Systems, 6(3), 2004, p. 1478-1482.
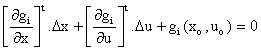 , i=1, ..., n
, i=1, ..., n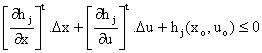 , j=1, ..., m
, j=1, ..., m