Modeling and Simulation of Air Pollutant Dispartion a Case Study of an Industrial Area in Nigeria
Mohammed ALHASSAN, AbdulFatai JIMOH
Department of Chemical Engineering, Federal University of Technology, Minna, Nigeria
mohakusi2003@yahoo.com, abdulfataijimoh@yahoo.com
Abstract
This work was carried out to develop a model equation for predicting air pollutant dispersion. Major air pollutant were identified, their source, how they cause air pollution, effects and control measures were analysed. Chemiluminecent analyser, non dispersive infrared analyzer (NDN), flame ionization detector, charcoal column absorber, and titration techniques were used for the analysis. Great emphasis was laid on the pollutants resulting from united African textile in Lagos State. A predictive model for air pollutant dispersion was developed and simulated using data collected from the industry for the year 2001, 2002 and 2003. Both the model and simulated result shows that pollutants such as NO, CO, and CO2 are dispersed in accordance with the law of the dispersion (which state that there is a trend in the reduction of pollutant concentration with increasing distance), The quantities of air pollutants emitted from the industries were compared with that of FEPA regulated emission limit for each pollutant and it was discover that UNTL Lagos at a certain point in time exceeded the regulated limits. Hence the model could be used in predicting air pollutant dispersion in air pollution control and the safe distance for human habitation from the industrial area.
Introduction
Industrialization is a prerogative for any country that intends to develop its economy. However, the move towards industrialization is not without its attendant problems. The increased industrial activities and increased population across the globe in addition to the rural-urban shift have created a situation whereby most of the people live in 1 percent of the nation’s land. All these factors have resulted in an increase in the stress on the environment as well as an increase in the concentrations of pollutants to a dangerous level, (Chinedu, 1991).
Lagos, a coastal state consists of Agege, Alimosho, Badagry, Epe, Eti-osa, Ibeju-lekki, Ikeja, Ikorodu, Lagos Island, Lagos Mainland, Mushin, Ojo, Oshodi/Isolo, Somolu and Surulere Local Government Areas. It has its capital in Ikeja. Lagos state, according to 1991 census figures has populations of 5,685,781 people, (National Population Census 1990). The yearly growth rate of population is equal with 2.83%. In the year 2000, it was predicted to be about 7,359,796 million people; it has an average population density of 1618 people per square kilometer. Lagos is the commercial as well as industrial nerve centre of Nigeria. This relatively small state is also home to over 50% of the industries in Nigeria. As a result, the state has the greatest problems of pollution, (National Population census 1990).
Air pollution can be defined as the condition that exists when the atmosphere contains a concentration of some substances that produces an objectionable effect, (Warner, 1976). As such, any large increase in concentration of a constituent of the air above its normal level could be considered an instance of air pollution, (Warner, 1976). There are two types of air pollution namely: indoor air pollution and ambient air pollution (Akinlotan, 1994), but this work is limited to ambient air pollution (outdoor air pollution),.
Automobiles, industries and electric power plants are the main sources of ambient air pollutants from man controlled processes. Volcanic actions, forest fibres and dust storm are natural sources of ambient air pollutants, but these contribute very little compared to the man-made source, (Agada, 2000).
The principal sources of emission in Lagos state is transportation (combustion of fuel), refineries, oils and distillates, evaporation during transfer and storage; industrial uses, wood (fuel and forest burning) incinerators and refuse burning and solvent evaporation, (Agada, 2000).
The major pollutants are gases and particulate matters, gases such as oxides of sulphur, nitrogen and carbon, ammonia and hydrocarbons. Other pollutants are particulate matters such as smoke, dust, fog, mist etc., (Agada, 2000).
Ambient air pollution is very hazardous; unfortunately, it is difficult to make definite statement about the precise health effects of ambient air pollution.
Methodology of Modelling
Modelling methodology is a process, which involves a number of clearly identifiable stages. Any model must have a definite purpose that is clearly stated at the start, (Koutitas, 1988).
Simulation
The implementation and validation of a model is the simulation. Simulation represent the application of modeling techniques to real systems, this enables information on the system to be gained without either construction or operating the full-scale system under consideration, (Koutitas, 1988). Simulation can be used to predict the effect of changing conditions to optimized operation quickly and safely and it can be used to provide in-depth knowledge about complete system behaviour, to improve and facilitate cost calculation and planning of operation. Simulation methods comes in two types viz Digital and analogue simulation. Of these two types, digital simulation which involves the use of code and programme are more in use since they can be implemented on modern computer with exceptional speed and accuracy, (Koutitas,1988).
Assumption made on the ambient air pollutant dispersion model
The assumptions made during the course of the development of this model are as stated below:
1. A mole of any gas occupies the same volume, i.e. the stack gases will occupy the same volume in the industrial are.
2. From Dalton’s law of partial pressure that states that for a mixture of gases, the total pressure is equal to the sum of the partial pressure of the constituent gases, in the same vein, it can be deduced that the total concentration of each gaseous pollutant example NO, CO and CO2.
3. It was assumed that the movement of the gas (diffusion) as a result of wind speed is a three dimensional movement i.e. all x, y and z (three dimensional) axes were considered for this model.
In the field, the phenomenon my have a fully three-dimensional nature (example a buoyant plume developing from stack emission), but in the far field, the horizontal motion prevails over the vertical. In the far field, the phenomenon can be two dimensional, in a horizontal sense.
4. The stack gases emitted from the industries to the atmosphere are not reactive i.e. there is no form of reaction between the pollutant.
Development of a mathematical model for air pollutants dispersion
This model is based on the expression for the mathematical model of a pollution transport using the Gaussian Distribution. Its expression was derived by De Moivre, Laplace in the seventeenth and eighteenth centuries. (Milton, 1995).
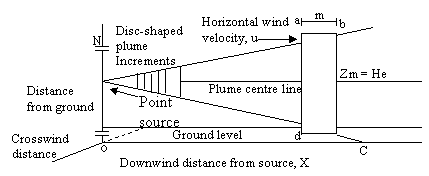
Figure 1. Cross section of a continuous point source of pollutants
Now, considering the population of a large class of objects, each class member possessing have some amount of measurable characteristic. The following definitions of the terminology involved are as follows:
- n1 is the population of a specific subclass
- l is the size of the subclass on the linear scale of the class characteristic
- xi is location of the specific subclass on the linear scale of the class characteristic.
![]() (1)
(1)
where σ = standard deviation
- Xm = the mean or arithmetic average value of the class characteristic amongst the total population
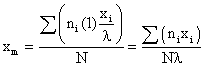
xi - xm = deviation amount of class characteristic between members of a subclass i and the main class m
σ = the standard deviation of the root mean square deviation from xm:
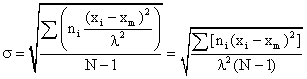
If λ of 1 $ /interval, 111/interval, then we can dispend with the λ term and equation 1 becomes:
![]() (1a)
(1a)
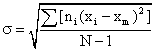
(xi - xm) and σ must both have the same units of dimension so the exponential term in the equation is dimensionless.
However, when dealing with stock gas dispersion, it is more useful to relate the population of a specific subclass (ni) to the total class population. Making (xi - xm) = U and integrating equation (1a) to obtain the area under the curve, which is the total class population N. Since the area is the summation of the rectangles having the height ni and the width Δu.
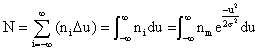
and the integration yields (using MathCAD):
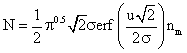
and further solved, with the limits (-¥ to ¥), gives:
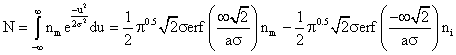
![]() (2)
(2)
Dividing equation (1a) by equation (2) we obtain:
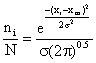 (3)
(3)
Equation (3) is the Gaussian distribution equation with the area under the curve equal to 1.
Finally, equation (3) is arranged to develop stack gas dispersion models based upon the Gaussian distribution.
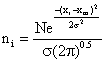 (4)
(4)
Neglecting the cross wind diffusion of the plane in Figure 1 and looking only at the total emissions as seen by viewing the vertical dimension from a far distance and hence the integrated cross wind emissions in the 1m thick increment a-b-c-d regardless of any diffusion in the Y – dimension. Applying the Gaussian distribution equation to eq. (4) we have:
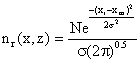
where: N = total grams of emissions in the entire 1 meter thick disc, zr = any receptor location (the small circle in fig) in the z - dimension where we want to determine emission density, zm = location of the mean emission density in the Z – dimension, σ2 = vertical standard deviation of the emission densities in meters (since λ = 1m/interval), In other words, the imaginary plume distribution is added to the actual plume, thus the Gaussian distribution in the vertical or z - dimension including upward reflector from the ground, become:
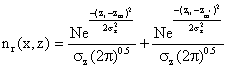 (5)
(5)
N = Q/u
zr - zm = Hr - He
zr - zm = Hr - (-He)
zr - zm = Hr + He
where Hr = height preceptor above ground, m.
Substituting the above parameters in to equation (5) yield:
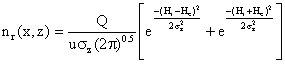 (6)
(6)
Now we can include the cross wind Gaussian distribution of nr (x, z) in the Y-dimension:
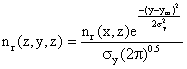 (7)
(7)
Finally, we can make this substitution into equation (6)
- C (concentration) = nr (x, y, z) to conform with convention
- Zr = Hr to conform with convention
- nr (x, z) = the right-hand side of equation (6)
- ym = O for the location of the mean emission density at the plume centreline in the cross wind or Y - dimension.
- y = distance from the receptor to the plume centreline in the cross wind or Y - dimension.
After making the above substitution into equation (7), we obtain the well - known generalized Gaussian Dispersion Equation for a continuous point - source plume of pollutants.
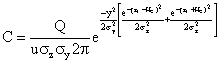 (8)
(8)
Equation (8) is the model equation for the concentration of pollutants at varying distances, where C = concentration of emission g/m3, at any receptor located at x = meters downwind, y = meters across wind from the centre line, zr = meters above ground; Q = Source emission rate g/sec; U = horizontal wind velocity m/sec; He =vertical standard deviation of the emission distribution, m; and σy = horizontal standard deviation of the emission distribution, m.
Experimental procedures
Reagents used were: Ozone, Hydrogen and oxygen or air, Non-absorbing Nitrogen gas contained in the reference cell
Apparatus used were: Chemiluminescent analyzer, Non dispersive infrared analyzer (NDIA), consist of a sample cell, two infrared source and a detector with two compartments, flame ionization detector, charcoal column absorber.
Determination of nitrogen oxides
Ozone was passed into the gaseous oxide this reacts rapidly with NO to form NO2 and oxygen. The emitted radiation from the reaction was received by a photomultiplier tube whose output was amplified and fed to a recorder. The intensity of radiation is proportional to the amount of nitric acid. The thermal converter incorporated into the chemiluminiscent analyzer enables the measurement of the level of NO2 content produced by taking the difference in readings when the gas flows through the converter and when it was passed, (Richardson, 1920).
Determination of carbon monoxide CO
An optical chopper alternatively exposes the reference and sample cells to the infrared sources. The reference cell passes almost all of the infrared energy into one compartment of the detector cell, while a varying amount of infrared energy, inversely proportional to CO concentration in the sample cell, reaches the other detector compartment, the CO contained therein expands causing a pressure differential across the diaphragm which in turn causes the diaphragm to pulse back and forth in phase with the chopper action. (The magnitude of the diaphragm distension is a function of the absorbing CO concentration in the sample cell). The mechanical movement of the diaphragm is concerted into an electrical signal which is amplified and recorded (Richardson, 1920).
Determination of hydrocarbons
Hydrocarbon pollutants can be determined as ‘total hydrocarbons’ or an individual chemical species. The most abundant hydrocarbon; methane is not a hazardous air pollutant and as such total hydrocarbon content is generally reported on a non-methane basis. The total hydrocarbon content is most commonly determined by the flame ionization technique.
The sample of gas containing the hydrocarbon was injected into the flame created by burning hydrogen in either air or oxygen in the flame ionization detector (FID). The presence of hydrocarbons makes the flame to produce a complex ionization in which large number of ions is present. An electric field was set up in the vicinity of the flame by making the burner jet positive with respect to a wire loop. The electric induces ion migration on such a manner that a small ionization current was established between the electrodes and this current is proportional to the concentration of iron in the flame. The current was amplified and displayed on an output meter.
The analysis of the non-methane hydrocarbon present is accomplished by a differential measurement. The sample is passed through a charcoal column which was saturated with methane but it is still capable of retaining other hydrocarbons. This column is then used with the FID as an analyzer for the analysis of methane only. Using the differences between the results obtained the non-methane hydrocarbons are assessed, (Richardson, 1920).
Results
Analysis of experimental and simulated result was carried out and the result are shown in tables 1 to 3.
Table 1. Concentrations of the pollutants in the year 2001
|
Dist (m) |
Experimental concentrations (mg/m3) |
Model concentrations (mg/m3) |
||||
|
NO |
CO |
CO2 |
NO |
CO |
CO2 |
|
|
0 |
2.411 |
5.627 |
4.019 |
2.401 |
5.617 |
4.009 |
|
10 |
0.02003 |
0.047 |
0.033 |
0.02 |
0.0470 |
0.0330 |
|
20 |
0.01021 |
0.024 |
0.017 |
0.01018 |
0.0240 |
0.0170 |
|
30 |
0.00691 |
0.016 |
0.012 |
0.00688 |
0.0160 |
0.0120 |
|
40 |
0.00524 |
0.012 |
0.009 |
0.00521 |
0.0120 |
0.0090 |
|
50 |
0.00423 |
0.01 |
0.007 |
0.0042 |
0.0100 |
0.0070 |
|
60 |
0.00355 |
0.008 |
0.006 |
0.00352 |
0.0080 |
0.0060 |
|
70 |
0.00306 |
0.007 |
0.005 |
0.00303 |
0.0070 |
0.0050 |
|
80 |
0.00269 |
0.006 |
0.004 |
0.00266 |
0.0060 |
0.0040 |
|
90 |
0.0024 |
0.006 |
0.004 |
0.00237 |
0.0060 |
0.0040 |
|
100 |
0.002 |
0.005 |
0.004 |
0.00197 |
0.0050 |
0.0040 |
|
FEPA LIMIT |
0.062 |
11.43 |
1.50 |
0.062 |
11.43 |
1.50 |
Table 2. Concentrations of the pollutants in the year 2002
|
Dist (m) |
Experimental concentrations (mg/m3) |
Model concentrations (mg/m3) |
||||
|
NO |
CO |
CO2 |
NO |
CO |
CO2 |
|
|
0 |
1.563 |
3.647 |
2.605 |
1.553 |
3.637 |
2.595 |
|
10 |
0.00993 |
0.023 |
0.017 |
0.0099 |
0.0230 |
0.0170 |
|
20 |
0.00501 |
0.012 |
0.008 |
0.00498 |
0.0120 |
0.0080 |
|
30 |
0.00337 |
0.008 |
0.006 |
0.00334 |
0.0080 |
0.0060 |
|
40 |
0.00255 |
0.006 |
0.004 |
0.00252 |
0.0060 |
0.0040 |
|
50 |
0.00205 |
0.005 |
0.003 |
0.00202 |
0.0050 |
0.0030 |
|
60 |
0.00172 |
0.004 |
0.003 |
0.00169 |
0.0040 |
0.0030 |
|
70 |
0.00148 |
0.003 |
0.002 |
0.00145 |
0.0030 |
0.0020 |
|
80 |
0.0013 |
0.003 |
0.002 |
0.00127 |
0.0030 |
0.0020 |
|
90 |
0.00116 |
0.003 |
0.002 |
0.00113 |
0.0030 |
0.0020 |
|
100 |
0.001 |
0.002 |
0.002 |
0.00097 |
0.0020 |
0.0020 |
|
FEPA LIMIT |
0.062 |
11.43 |
1.50 |
0.062 |
11.43 |
1.50 |
Table 3. Concentrations of the pollutants in the year 2003
|
|
Experimental concentrations (mg/m3) |
Model concentrations (mg/m3) |
||||
|
Dist (m) |
NO |
CO |
CO2 |
NO |
CO |
CO2 |
|
0 |
1.939 |
4.524 |
3.231 |
1.929 |
4.514 |
3.221 |
|
10 |
0.01398 |
0.033 |
0.023 |
0.01395 |
0.0330 |
0.0230 |
|
20 |
0.00709 |
0.017 |
0.012 |
0.00706 |
0.0170 |
0.0120 |
|
30 |
0.00478 |
0.011 |
0.008 |
0.00475 |
0.0110 |
0.0080 |
|
40 |
0.00362 |
0.008 |
0.006 |
0.00359 |
0.0080 |
0.0060 |
|
50 |
0.00292 |
0.007 |
0.005 |
0.00289 |
0.0070 |
0.0050 |
|
60 |
0.00245 |
0.006 |
0.004 |
0.00242 |
0.0060 |
0.0040 |
|
70 |
0.00211 |
0.005 |
0.004 |
0.00208 |
0.0050 |
0.0040 |
|
80 |
0.00185 |
0.004 |
0.003 |
0.00182 |
0.0040 |
0.0030 |
|
90 |
0.00165 |
0.004 |
0.003 |
0.00162 |
0.0040 |
0.0030 |
|
100 |
0.001 |
0.003 |
0.002 |
0.00097 |
0.0030 |
0.0020 |
|
FEPALIMIT |
0.062 |
11.43 |
1.50 |
0.062 |
11.43 |
1.50 |
Discussion of results
The model equation developed for predicting air pollutant dispersion is given by:
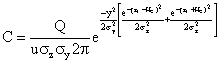
This equation was used in the simulation of result for air pollutant dispersion presented the tables above for three consecutive years.
Analysis of both the tables shows that the concentration of pollutants were beyond the standard limit allowed by FEPA at the point of discharge, except for carbon monoxide, CO, which is still within the FEPA limit. For instance, in table 1, the concentration of NO was 2.401mg/m3, CO was 5.617mg/m3 and CO2 was 4.009mg/m3 from the predicted model while NO was 2.411, CO was 5.627, and CO2 was 4.019mg/m3 respectively from the experimental result.
In table 2, the concentration of NO was 1.563, CO was 3.647, and CO2was 2.605 from the experimental result while for the model equation the concentration were found to be 1.583 for the NO, 3.637 for CO and 2.595 mg/m3 for CO2 respectively.
Table 3 shows that from the experiment, the concentration of pollutant at the point of discharge were 1.937 for NO, 4.524 for CO and 3.231 for CO2 respectively, while for predictive model, the concentration were found to be 1.929 for NO 4.514 for CO and 3.221 for CO2 respectively. How ever these values were beyond FEPA limit of 0.062mg/m3for NO, 11.43mg/m3 for CO and 1.50mg/m3 for CO2 respectively.
Detail investigation of the three tables shows that the concentration of these pollutants decrease with increase in distance traveled from the point of discharge. For instance, table 1 shows that from the model equation the concentration of NO, was 2.401mg/m3 at the point of discharge, but decreased to 0.0042mg/m3 and 0.0019mg/m3 at 50m and 100m away from point of discharge. This shows that the pollutants diffuse gradually with time to any point as long as there is wind. Comparisons between the simulated and experimental result shows that both results are in agreement with each other which prove that air pollutant dispersion can be predicted using the model developed.
However, the level of ambient air pollution in Lagos metropolis can be reduced or controlled by proper monitoring of the industries operating within the area to make sure that they comply with FEPA standard. The mathematical expression developed can, as well, go along way to control the pollution because if the concentration of pollutants at certain region is known, effort can be geared towards preventing further dispersion from point of discharge to the areas yet to be polluted.
Conclusions
From the results of the dispersion model, it is obvious that the aims of this work were to a great extent achieved. The model was developed and was used in the simulation of data obtained from an industrial area, and analysis of the result showed that the model can be used in predicting the amount of air pollutants emitted into the surrounding environment with respect to distances from the point of emission, and the result showed the trend in the reduction of the pollutant concentration with increasing distance, which conform and support the validity and authenticity of the dispersion model Hence the model can effectively be used to determine the safe distance for human habitation from any industrial area with knowledge of tolerant emission limit from the pollution regulation body (FEPA).
References
[1] Adegbe A. D. S., Air Pollution Modelling of an Industrial City (A Case Study of Kaduna Industrial Area), B. Eng, FUT, Minna, Nigeria, pp.39-45 & 60-72, 2000.
[2] Olufunke A. J., A Review of Method of Air Pollution Control, B. Eng, University of Lagos, Lagos Nigeria, pp. 4-45, 1994.
[3] Thompson C. P., An Assessment of Air Pollution in Lagos Metropoly, B. Eng., University of Lagos, Lagos, Nigeria, pp. 22-49, 1991.
[4] Koutitas C. G., Mathematical Models in Coastal Engineering, Wiley Publishers, New Delhi, pp.49, 1988.
[5] Milton R. B., Fundamentals of Gas Dispersion, Irvine, California, pp.21-51, 1995.
[6] Nigeria National 1990 Population Census, Government Press, Lagos 1993.
[7] Richardson L. F., Experiments on the Diffusion of Smoke Emitted from a Fixed Point, Phil. Trans. A, Britain, 1920, 221, p. 1.