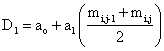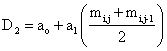Numerical Simulation of Moisture Transfer in Wood Drying in Open-Wall Timber Shades
Vincent Obiajulu OGWUAGWU
Mechanical Engineering Department, Federal University of Technology, Minna, Nigeria
Abstract
A numerical simulation of moisture transfer in wood drying in open-wall timber shades in Nigeria is presented. Results show that wood dried under this condition usually dry at a very slow rate, hence requiring a very long period of drying time. The results also explain why there are high incidence of warping in rafters, purlins and facing boards commonly used in roof construction throughout the country.
Keywords
Moisture transfer, Rafters, Purlin, Wooden Board, Warp
Introduction
The role of wood in the construction of houses in both developed and developing nations cannot be overemphasized. When lumber is fell down and sawn into thick or thin sections (such as rafters, purlins and boards), they are usually allowed to dry before they are used in the construction of roofs or walls. The drying process can take place under controlled conditions or in open air or under shade, such as open-wall houses used in local “timber shades”. In both cases, as is the practice in most developing countries, the drying rate is not usually controlled.
They are usually arranged in heaps, in-between supporting sticks driven into the soil to prevent them from falling off the heap. Wood drying under this uncontrolled rate may lead to some drying defects. Most at times the ones completely enclosed in the heap usually have high moisture content even at the time of sales. Some of the wood that are well exposed may dry at a faster rate and often develop such defects as checks, splits and wraps.; which may be as a result of drying stresses developed from moisture gradients or restrained shrinkage within the wood.
According to Rice (1988) improving drying time and quality depends on the understanding and controlling of moisture movements in wood during drying. Different techniques are available for determining moisture movement in wood during drying. Many researches have been carried out on the difference of diffusion coefficient, water conductivity and shrinkage between the radial and tangential directions (Clouties and Fortin, 1993; Li and Plumb, 1994; Wu and Milota, 1995, and Shupe et al., 1995). Also, Williams (1992), studied moisture content of 13 eastern red cedar heartwood samples using both the distillation and oven-drying methods and concluded that the distillation method gave more accurate results. In the present work, a numerical study of moisture movement in pile of wooden boards (commonly used as facing boards in buildings) dried in an open-wall timber shade is presented.
Theory of Wood Drying
The principles of moisture movement in wood and the major factors affecting the movement were given by Hart (1964). According to him, moisture movement for the unsteady state can be divided into two parts: firstly, moisture gradient advanced from the surface to the center of the specimen with no attendant moisture change occurring at the center and secondly, the moisture gradient reached at the center approaching equilibrium. He gave the expression for calculating moisture gradient during the second part as:
|
|
(1) |
where Mx = moisture content at depth x; Ma = moisture content at the center, a; and Mo = equilibrium moisture content on the surface of wood.
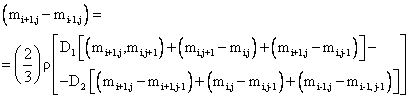
Chen et al. (1996) later developed a numerical analysis technique to evaluate the moisture dependent diffusion coefficient using drying curves. This method gave an accurate prediction of moisture movement throughout the entire drying process. They used the three-level finite difference given in equation (2) to obtain the moisture profile in wood during drying.
|
|
(2) |
with:
|
|
(3) |
|
|
(4) |
|
|
(5) |
where m is the fractional moisture based on the over-drying weight, t is the drying time and x is taken in a direction along the thickness of the sample; i,j refer to the location of m along the t and x coordinates.
Commers and Mclain (1988) carried out a study on modeling moisture gradient effects on bending properties of wood. They modified the common one-dimensional parabolic model for moisture distribution in drying wood to a two-dimensional model given as:
|
MC = 2.25(MC - EMC)(1.0-k1x2)(1.0k2y2) + EMC |
(6) |
where: MC = percentage moisture content at coordinates x,y; MC = average moisture content; EMC = percentage equilibrium moisture content; x = horizontal distance from the centroid; y = vertical distance from the centroid; k1 = 1.0/(w/2); k2 = 1.0/(d/2) with w = width of the cross-section, and d = depth of the cross section.
In the present study, a numerical simulation of moisture distribution in a pile of wooden boards as illustrate in Figure 1 was carried out using the following conservation of mass equation:
|
|
(7) |
where Pv = vapour pressure; μ = permeability; Pl = capillary pressure; k = hydraulic conductivity; γ = moisture content; y = distance, and t = time.
Figure 1. Pile of wooden boards being dried in open wall timber shade
Results and discussion
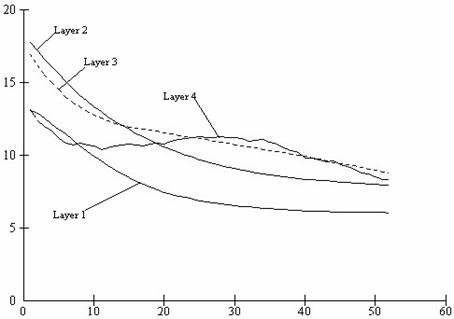
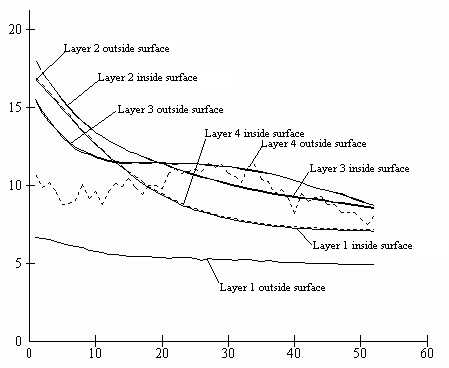
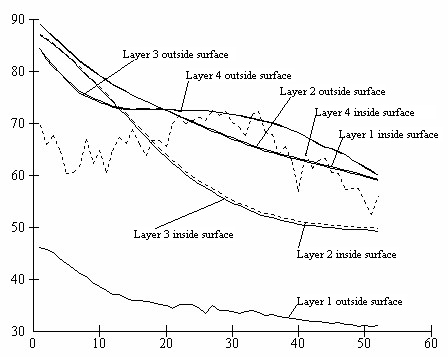
Figures 2 to 7 shows the results obtained from the numerical simulation. Figure 2 show the instantaneous layer moisture distribution during the drying period while figure 3 show the instantaneous surface moisture distribution during the drying process.
|
Instantaneous layer moisture condition |
|
|
|
Weeks |
Figure 2. Instantaneous layer moisture condition
|
Instantaneous surface moisture condition |
|
|
|
Weeks |
Figure 3. Instantaneous surface moisture condition
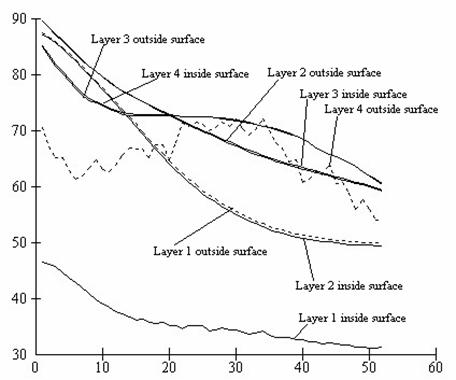
The instantaneous surface relative humidity is as shown in figure 4 while the time-average relative humidity is as shown in figure 5.
|
Instantaneous relative humidity |
|
|
|
Weeks |
Figure 4. Instantaneous surface relative humidity
|
Time-average surface relative humidity |
|
|
|
Weeks |
Figure 5. Time-average surface relative humidity
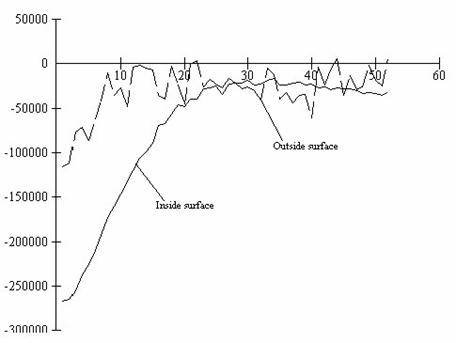
The surface moisture fluxes are shown in figure 6. The temperature distribution at the surfaces of the wooden boards is as shown in figure 7.
|
|
Weeks |
|
Surface moisture fluxes |
|
Figure 6. Surface moisture fluxes
|
Surface temperatures |
|
|
|
Weeks |
Figure 7. Surface temperatures
From the graphs of both moisture and relative humidity distribution during the drying process, it is obvious that these wooden boards are actually subjected to relatively very slow drying rates. This reason explains why some of these wooden boards and purlins normally warp when they are used in roofing houses. This is because enough time has not been allowed for the wood to dry completely. The fast drying rates to which they are subjected when used in roofing normally results in defects.
The temperature distribution shows that during the raining season temperature within the layers are usually relatively low, which would also slow down the drying rate. Hence, the higher incidents of defects in wooden purlins and facing boards when they are acquired from these Timber Shades for roofing during this period of the year.
Conclusions
Although a numerical simulation approach has been used in the present study, the results obtained actually explains the high incident of defects occurring when wooden products are procured from the local Timber shades for roofing houses. Also, based on these results, it is advisable that wooden products obtained from these sources be allowed to dry properly in the open air for some time before using them for roofing applications.
References
1. Chen Y., Choong E. T., Wetzel D. M., A numerical analysis technique to evaluate the moisture-dependent diffusion coefficient on moisture movement during drying, Wood and Fiber Science, 1996, 28(3), p. 338-345.
2. Cloutier A., Fortin Y., A model of moisture movement in wood based on water potential and the determination of the effective water conductivity, Wood Science and Technology, 1993, 27(2), p. 95-114.
3. Conners T. E., McLain T. E., Modeling moisture gradient effects on bending properties, Wood and Fiber Science, 1988, 20(2), p. 226-242.
4. Hart C. A., Principles of moisture movement in wood, Forest Products Journal, 1964, 14(5), p. 207-214.
5. Li G., Plumb O. A., The effect of heterogeneity on wood drying. Part II: Experimental results, Drying Technology, 1994, 12(8), p. 2003-2026.
6. Rice R. W., Mass transfer, creep and stress development during the drying of red oak, Ph.D Dissertation, 153 pages, Virginia Polytechnique Institute and State University, Blacksburg, Virginia, 1988.
7. Shupe T. F., Choong E. T., Gibson M. D., Differences in moisture content and shrinkage between outerwood, middlewood and core wood of two yellow-poplar trees, Forest Prod. J., 1995, 45(9), p. 85-90.
8. William B. S., Determining moisture content in eastern redcedar, Forest Products Journal, 1992, 42(7), 67-69.
9. Wu Q., Milota M. R., Shrinkage and set in drying of 4 by 4 Douglas-fir lumber, Forest Prod. J., 1995, 45(5), p. 59-63.