The Investigation of Furnace Operating Characteristics Using the Long Furnace Model
Shuaibu Ndache MOHAMMED
Department of Mechanical Engineering, Federal University of Technology, Minna, Nigeria
Abstract
This work reports the results of the numerical evaluation of some furnace operating characteristics by use of the ‘long furnace model’. The furnace characteristics considered include the furnace output, efficiency, heat input, stock emissivity and line speed. In this analysis, it is found that the computed wall to stock view factors differ from those obtained by graphical method in the range of 0 - 0.46%. This suggests that computed results could be used with confidence. The effects of stock emissivity on both the furnace efficiency and output increased as the furnace zones increase. Furnace performances are influenced by the heat input to the enclosure with the maximum performance being at a heat input of 700kW. It was found in all analyses that the higher the number of furnace zones, the better will be the furnace performance.
Keywords
Long Furnace Model, Stock Emissivity, Absorbing Medium, Mean Beam Lengths, Efficiency, Output, Heat Input, Number of Zones
Introduction
In high temperature furnaces, that is, above about 800ºC (1073K), radiation can be the dominant mode of heat transfer and a considerable effort has been expended in developing methods of estimating rates of radiative heat exchange in these furnaces. The methods are also valid for lower temperatures but in these cases, combined effects of convective and radiative heat transfer must be taken into account. The calculations enable furnace performance to be predicted rapidly and reliably without using experimental furnaces, thus avoiding inherently large costs of the latter (Gray and Muller, 1974).
In 1986, Tucker observed that in systems with large temperature gradients, subdivision of the furnace into zones may be necessary and the variations of emissivity and/or absorptivity will be required over a range of beam lengths and temperatures.
In 1972, Pantakar and Spalding presented a form of solution for the radiant heat exchange within an enclosure using the zoning method while utilizing the method applied by Hottel and Cohen (1958). Matsunga and Hiraoka (1972) used experimental modeling for the simulation of gas flow patterns in a reheating furnace. They observed that consideration of flow patterns may lead to some design alterations so as to prevent local flame impingement and consequent overheating of the walls and stock. They also concluded that model studies are useful in assessing the degree of uniformity of heating in furnaces.
The processes in a furnace are highly complicated for example, the flow distribution can be turbulent, three dimensional and there is formation and extinction of soot continuously (luminosity). Thus, comprehensive modeling is difficult; however, other less involved models can be used to investigate furnace performance. Useful predictions of overall furnace performance have been obtained with these simple models. These assume that the gas composition is uniform and that the temperatures of the gases and furnaces remain invariant.
Long Furnace Model
In a continuous furnace, stock enters one end at a low temperature and emerges at a high temperature. Thus, there are substantial changes in surface and gas temperatures along the furnace. If the furnace length is large compared to the cross-sectional dimensions, temperature gradients will also occur and the simplest model to use in this case is the ‘plug flow’ model. The gases are assumed to flow along the furnace as a plug with constant transverse temperatures and compositions. The furnace geometry is divided into sections called zones as shown in Figure 1.

Figure 1. A Schematic of the Long Furnace Model
Each surface and the gas volume within each section (zone) is assumed to be isothermal. The length of the individual sections depends upon the closeness with which the temperature gradient in the furnace is to be modeled. The simplest form of calculation considers each section to be thermally isolated, that is, the boundaries between each section and its neighbours are considered to be adiabatic walls across which there is no net heat transfer. This model is usually called the ‘long chamber’ or ‘long furnace model’. If the side walls are totally reflecting refractories, the four walls of the section may be possible to treat the roof in the same way. The analysis then becomes similar to the well-stirred model, a separate calculation being performed for each section (zone). In addition, when there are significant temperature variations throughout an enclosure, it becomes necessary to subdivide (conceptually) the enclosure into large (n) surface zones, each zone being characterized by the near constancy of its temperature and emissivity. For n surfaces, n2 view factors have to be determined.
Heat transfer calculations can be carried out by assuming that:
· Temperature and concentrations vary only along the length of the furnace.
· Gaseous radiation (i.e. non-luminous flame has small beam length) is neglected.
Consequently, each zone may be analyzed as follows (see figure 2):
|
Heat transfer to surface = Heat released + Heat input from previous section - - Heat lost by gases flowing out of section |
|
That is:
|
Heat input - Heat in exiting gases = Heat transfer in zone Qin - n(mCp)(Tg-Ti)/N = hwAw(Tg-Tw) + hsAs(Tg-Ts) |
(1) |
where n is the zone number, that is, n = 1, 2, 3, …, and N is the total number of zones. Qin for the first zone is assumed to be Qin/N and that for subsequent zones being Qin. The initial and final temperatures (Ti & Tf) of the stock are assumed, while the stock temperature in each zone Ts is calculated as follows:
|
Ts(i+1) = T*s(i) - ΔTs, i = 1, 2, 3, …, (N+m-1) |
|
where T*s(i) = {Tf + Ts(i) )/2 and ΔTs = (Tf – Ti)/(N+m)

Figure 2. Long Furnace Zone Heat Balance
There are two unknown temperatures, Tg, gas temperature, and Tw, roof temperature, for each zone.
A heat balance on the adiabatic refractory roof provides a second equation. The roof and stock surfaces may be considered as two parallel planes. Therefore,
|
σAwFws[T4w - T4s] / [1/Єw + 1/ Єs - 1] = hwAw(Tg - Tw) |
(2) |
Heat balance equations are then solved for unknown gas temperatures. Thus, the temperature distribution is approximated by a series of steps. The shorter the steps, the more accurate the solution is. Unequal steps can be used, for example, short steps in regions of high temperature gradients or heat release. Changes in flame length may be allowed for by altering gas composition along furnace length.
If radiation between different sections is ignored, a single marching solution from the initial zone is possible and this is often sufficiently accurate for practical purposes.
Nevertheless, exchange between different sections can be allowed for although the complexity of the problem increases since:
· It is difficult to determine exchange area factors;
· Energy balance in each zone/section contains all the gas temperatures and not just the temperature at the zone under examination. Hence equations must be solved simultaneously.
Equations (1) and (2) were solved for temperature values Tw and Tg using the modified Newton-Raphson method because of the non-linearity of variables in the simultaneous equations.
Furnace Efficiency
This is obtained as the ratio of the total heat transfer to zones to the total heat input to the furnace.
That is
|
ηth = ∑Qz / Qin |
(3) |
and
|
Qz = hwAw(Tg - Tw) + hsAs(Tg - Ts) |
(4) |
for each zone.
Furnace Output
This is the ratio of the total heat transfer to zone to the heat content of stock. Its unit is kilogram per second (kg/s). That is
|
Output = ∑Qz / Qc |
(5) |
where Qc = Cp(Tf – Ti)
Line Speed
It is the ratio of furnace output to the product of stock cross-sectional area and the density.
That is:
|
Speed = output / (Asρs) |
(6) |
Its unit is meter per second (m/s)
It is therefore evident that the correctness of furnace efficiency, output and line speed which are the major parameters governing the furnace performance require that the gas and roof temperatures be accurately determined.
Effect of an Absorbing Medium on the Radiative Heat Transfer within an Enclosure
If an absorbing medium is present in the enclosure described by Mohammed (1988) is still valid but
· Radiation passing from one surface to another is attenuated by the medium; and
· By virtue of its temperature, the medium itself radiates energy to each surface.
The governing equations for this analysis are:
|
Hi = ∑nj=1 WjFijτij + Mi |
(7) |
where τij is the transmissivity of the medium between surfaces i and j and Mi is the flux emitted by the medium which is incident upon surface i. Mi can be written as εmEbm so that equation (7) becomes:
|
Hi = ∑nj=1 WjFijτij + εmEbm |
(8) |
where εm is the emissivity of the medium and Ebm is the black-body emissive power of the medium.
The emissivity of the medium is defined by:
|
εm = 1 - e-(KLms) |
(9) |
where Lms is the mean beam length evaluated by considering the radiation from the medium to the surface.
The transmissivity τij in equation (19b) is defined by:
|
τij = e-(KLij) |
(10) |
where Lij must be determined by considering radiation from surface i which is transmitted to surface j. Dunkle (1964) has computed values of Lij for parallel and perpendicular plate geometries.
The geometrical configurations of greatest interest are those for radiation between two rectangles, either parallel or at right angles (Dunkle, 1964; Bevans & Dunkle, 1960; Oppenheim & Bevans, 1960). For parallel rectangles with equal sides of lengths a and b and spaced a distance c apart (Fig. 3a), the dimensionless mean beam length parameter
|
Lij = (Far)ij / (abc) |
(11) |
in terms of the edge distance ratios X = a/c, Y = b/c is given by
|
Lij = FArij/abc = = 4/πtan-1[XY/√(1 + X2 + Y2) + 1/X ln[(X+ √(1+X2 +Y2 ))/ /((√(1 + X2 )(Y + √(1 + Y2 ))] + 1/Y ln[(X + √(1 + X2 + Y2 ))/ /((√(1 + Y2 )(X + √(1 + X2 ))] + 1/XY [√(1 + X2 ) + √(1 + Y2 ) - -1 - √(1 + X2 + Y2 )] |
(12) |
The equation for the geometric mean beam length parameter Lij for rectangles ab and bc at right angles with a common edge b (Figure 3b) is expressed in terms of the length ratios X = a/b and Y = c/b as follows:
|
Lij = FArij/abc = 1/π Y/X ln [{1+ √(1 + Y2) √(X2 + Y2))/(Y(1 + √(1 + X2 + Y2))] + a/Y ln[{1+ √(1 + X2) √(X2 + Y2))/ (X(1 + √(1 + X2 + Y2))] + + 1/3XY[(1 + Y2)3/2 +(1 + X2)3/2 + (X2 + Y2)3/2 - (1 + X2 + Y2)3/2] + + X/Y[√(1 + X2 + Y2) - √(X2 + Y2) – √(1 + X2)] + Y/X[√(1 + X2 + Y2) - √(X2 + Y2) – √(1 + Y2)] + 3/2[Y2/X2 + X2/Y - 1/2XY] |
(13) |
Figure 3a. Identical, Parallel Rectangular Plates
Figure 3b. Touching Inclined Plates
Computer Program
With the increasing availability of high speed digital computers, attention has turned to the development of computer programs capable of calculating accurately the combustion within furnaces.
The program for the analyses evaluates the gas and wall temperatures of the furnace enclosure, Tg and Tw by calling SUBROUTINE SOLVE. It, therefore, analyses furnace performance while employing zoning technique. In all, the program calls two subroutines, vis-a-viz: SUBROUTINES SHAPEX and SOLVE. The following parameters were varied using this program:
(i) Number of zones, N;
(ii) Total heat input, QQ; and
(iii) Stock emissivity, Es.
Results and Discussion
The Long Furnace Model Analysis
The numerical results obtained using the computed wall to stock view factors and those obtained by graphical method compare favorably well with difference in values ranging from 0 - 0.46%; an indication that the present numerical results can be used with confidence (see Tables 1 and 2, respectively).
Table 1. Numerical Results for the Long Furnace Model Analysis
|
Zone |
Heat Transfer (kW) |
Heat input (kW) |
Roof Temp. (K) |
Gas Temp. (K) |
|
1 2 3 4 5 6 |
113.108 126.460 139.471 152.226 54.424 50.465 |
220.000 326.892 420.432 500.961 348.735 294.311 |
1221.594 1158.015 1100.737 1048.383 843.033 768.136 |
1379.720 1312.283 1245.998 1180.644 1043.210 915.772 |
Table 2. Graphical Results for the Long Furnace Model Analysis
|
Zone |
Heat Transfer (kW) |
Heat input (kW) |
Roof Temp. (K) |
Gas Temp. (K) |
|
1 2 3 4 5 6 |
113.5 126.5 139.3 151.8 54.7 50.7 |
220.0 326.5 420.0 500.7 348.9 294.2 |
1216 1153 1098 1048 841 766 |
1378 1310 1245 1181 1043 915 |
In this analysis, the effects of changes in some of the furnace conditions were considered. These are discussed below:
Stock Emissivity
The effects of stock emissivity on efficiency and output are shown on Figures 4 and 5 respectively, for different number of furnace zones. It is observed from all the figures that an increase in stock emissivity results in a corresponding increase in efficiency and output.
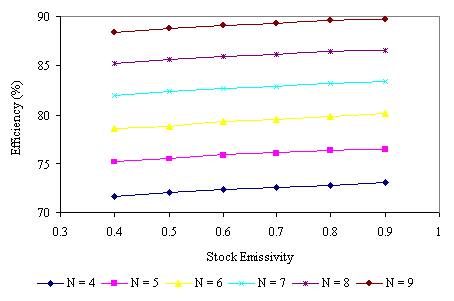
Figure 4. Effect of Stock Emissivity on Furnace Efficiency
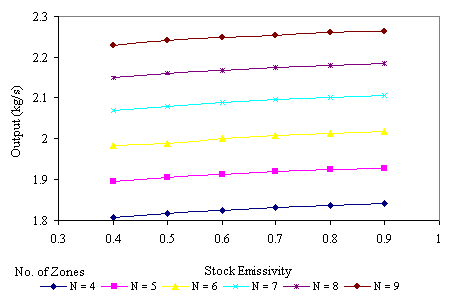
Figure 5. Effect of Stock Emissivity on Furnace Output
Heat Input
Figures 6 and 7 show the effect of heat input on efficiency and output for furnace zones ranging from four to nine respectively. It is evident that an increase in heat input initially produces an increase in the output with sudden sharp reduction on passing the peak value at a heat input value of approximately 700kW. The efficiency, however, decreases with increasing values of the heat input.
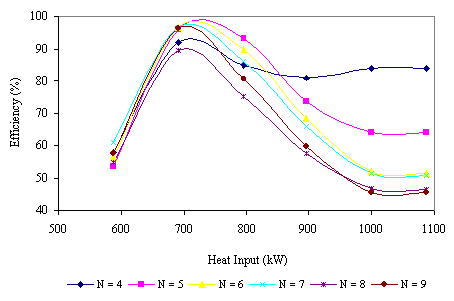
Figure 6. Effect of Heat Input on Furnace Efficiency
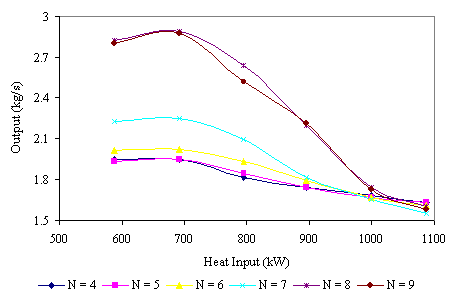
Figure 7. Effect of Heat Input on Furnace Output
Number of Zones
The effects of number of zones on furnace performance are presented in Figure 8.
It can be observed that an increase in furnace number of zones is accompanied by a simultaneous increase in furnace efficiency and output. Hence, the more the number of zone divisions, the better the furnace efficiency and hence performance. However, for practical purposes the number of zones cannot be increased indefinitely. Also, the computer (and hence the cost) increases with the number of zones. Thus, it is essential to predetermine (or stipulate) the maximum number of zones for any furnace system.
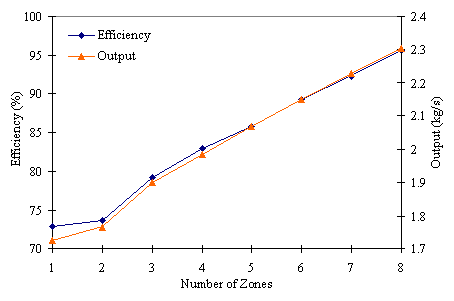
Figure 8. Effect of Number of Zones on Furnace Performance
Mean Beam Lengths
In evaluating the heat transfer for the absorbing medium, it was necessary to determine the mean beam lengths for the surfaces. This was carried out and the results are as presented in Table 3. It can be observed that the results are symmetrical about the diagonal so that Lij = Lji.
Table 3. Computed Surface to Surface Mean Beam Lengths
|
L |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
3.400 |
2.623 |
1.120 |
1.120 |
1.120 |
1.120 |
|
2 |
2.623 |
3.400 |
1.120 |
1.120 |
1.120 |
1.120 |
|
3 |
1.120 |
1.120 |
6.800 |
2.503 |
0.961 |
0.961 |
|
4 |
1.120 |
1.120 |
2.503 |
6.800 |
0.961 |
0.961 |
|
5 |
1.120 |
1.120 |
0.961 |
0.961 |
5.100 |
2.412 |
|
6 |
1.120 |
1.120 |
0.961 |
0.961 |
2.412 |
5.100 |
Conclusions
This work is based on the application of the ‘long furnace model’ which incorporates computed view factors and means beam lengths that were used in the evaluation of radiation exchange within rectangular non-absorbing or gas-filled enclosures.
Also, the analysis embarked upon on heat transfer within a furnace using simple models such as the ‘long furnace model’ could enable furnace behavior to be analyzed in a semi-rigorous, but probably adequate fashion. Based on all results obtained it became evidently clear that the model, which is numerical in application can handle much more complex geometry/thermal systems within a small time interval; hence it is time saving as compared to the traditional graphical method. The method, therefore, allows for proper furnace analysis as regards the radiative heat transfer in an absorbing enclosure. The method can also handle different furnace geometries.
References
[1] Bevans J. T., Dunkle R. V., Radiant Interchange within an Enclosure, Journal of Heat Transfer, Trans. ASME, Series C, Vol. 82, 1960, p. 1-19.
[2] Becker H. B., A Mathematical Solution for Gas-to-surface Radiative Exchange Area for a Rectangular Parallelopiped Enclosure Containing a Gray Medium, ASME, Journal of Heat Transfer, Vol. 99, 1977.
[3] Dunkle R. V., Geometric Mean Beam Lengths for Radiant Heat Transfer Calculations, Journal of Heat Transfer, ASME Series, 86(1), 1964, p. 75-80.
[4] Gray W. A., Muller R., Engineering Calculations in Radiative Heat Transfer, Pergamon Press Ltd., Vol. 13, 1974, p. 1-75.
[5] Mohammed S. N., Mathematical Modeling of Furnaces, Research Report, of Ibadan, Ibadan, 1988.
[6] Oppenheim A. K., Bevans J. T., Geometric Factors for Radiation Heat Transfer Through an Absorbing Medium in Cartesian Co-ordinates, Journal of Heat Transfer, Trans. ASME, Series C, vol. 82, 1960, p. 360-368.
[7] Patankar S. V., Spalding D. B., Mathematical Models of Fluid Flow and Heat Transfer in Furnaces: A Review, Paper 2, 4th Symposium on Flames and Industry, 1972.
[8] Tucker R. J., Direct Exchange Areas for Calculating Radiation Transfer in Rectangular Furnace, Journal of Heat Transfer, ASME, vol. 108, 1986, p. 707-710.