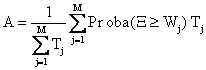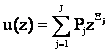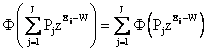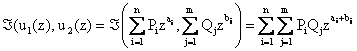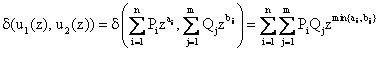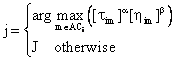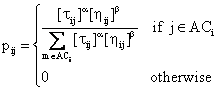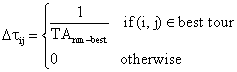Hybrid Approach for Redundancy Optimization of Multi-State Power System
Omar BENDJEGHABA1, Dris OHAHDI1, Abdelkader ZABLAH2
1Department of Electrical Engineering, University of Boumerdes , Algeria
2Department of Electrical Engineering, University of Sidi Belabes, Algeria
benomar75@yahoo.fr, azeblah@yahoo.fr
Abstract
This paper presents an optimize method of the well known Redundancy Optimization Problem (ROP) using a combined ANT Colony System (ACS) and Universal Moment Generating Function (UMGF). The ACS searches for the minimum cost solution by selecting the appropriate components for a series-parallel system, given a minimum system reliability constraint. The UMGF is used to estimate the system reliability value during search. This approach is an example of a computationally efficient method to apply ACS optimization to problems for which repeated calculation of the objective function is impractical.
Key words
Ant colony System (ACS), Redundancy Optimization Problem (ROP), Multi-State Power Systems (MSPS), Universal Moment Generating Function (UMGF)
Introduction
Many of modern Power systems can perform the task at several different levels. In this case the system failure can lead to decreased capability to perform a given task, but not to complete failure. In addition, every system element also can perform its task with some different levels. For example, Power plant unit has its nominal generating capacity. If there are no failures the nominal capacity is available. Some kinds of failures can cause the complete unit outage while for some other failures the unit can work with reduced capacity. A system which can have some different task performance levels is named Multi-State Power System (MSPS).
This paper uses an ACS combined with Ushakov‘s technique to solve the ROP for MSPS. The idea of employing ants of cooperating agents to solve combinatorial optimization problems was recently proposed in [1]. The ACO has been successfully applied to the classical traveling salesman problem in [2], to the quadratic assignment problem in [3], and to scheduling in [4]. Ant algorithm shows very good results in each applied area. It has been recently adapted for the reliability design of binary state systems in [5]. The ACO has also been adapted with success to other combinatorial optimization problems such as the vehicle routing problem in [6], telecommunication networks management in [7], and graph coloring in [8].
The remainder of this paper is organized as follows: In section 2, the Redundancy Optimization problem formulation is formulated. In section 3, the reliability estimation based on Ushakov’s technique is developed. In section 4, the ant algorithm is adapted to solve the Cost Structure Optimization Problem of MSPS. In section 5, illustrative example and numerical results are presented and discussed. Conclusions are drawn in section 6.
Formulation of the redundancy optimization problem
Series-parallel system with different redundant elements
Let consider a series-parallel system
containing n subcomponents Ci (i = 1, 2,
…, n) in series as represented in Figure 1. Every component Ci
contains a number of different elements connected in parallel. For each
component i, there are a number of element versions available in the
market. For any given system component, different versions and number of
elements may be chosen. For each subcomponent i, elements are
characterized according to their version v by their cost (Civ),
availability (Aiv) and performance (Xiv). The structure of system component ![]() can be defined by the numbers
of parallel elements (of each version)
can be defined by the numbers
of parallel elements (of each version) ![]() for
for ![]() , where
, where ![]() is a number of
versions available for element of type i. Figure 1 illustrates these
notations for a given component i. The entire system structure is
defined by the vectors ki = {kiv}
(1 ≤ i ≤ n, 1 ≤v ≤ Vi).
is a number of
versions available for element of type i. Figure 1 illustrates these
notations for a given component i. The entire system structure is
defined by the vectors ki = {kiv}
(1 ≤ i ≤ n, 1 ≤v ≤ Vi).
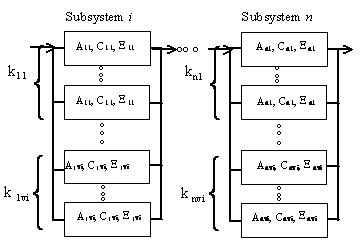
Figure 1. Structure of series parallel System
For a given set of vectors k1, k2, …, kn the total investment cost of the system can be calculated as:
|
|
(1) |
The problem of total investment-cost minimization, subject to reliability or availability constraints, is well known as the redundancy optimization problem (ROP).It can be formulated as follows: find the Structure (topology) corresponding to the minimal total cost, such that the corresponding reliability A exceeds or equal the specified desired A0:
Minimize
|
|
(2) |
Subject to
|
A ≥ A0 |
(3) |
System Reliability
In electric power systems, reliability is considered as a measure of the system ability to meet the load demand (W), i.e., to provide an adequate supply of electrical energy (X). This definition of the reliability index is widely used for power systems: see e.g., [9], and [10]. The Loss of Load Probability index (LOLP) is usually used to estimate the reliability index in [11]. This index is the overall probability that the load demand will not be met. Thus, we can write A = Proba (X ³ W) and the LOLP= 1-A . This reliability index depends on consumer demand W.
For reparable MSS, a multi-state steady-state availability E is used as Proba (X ³ W). In the steady-state the distribution of states probabilities is given by equation (4), while the MSS stationary reliability is formulated by equation (5):
|
|
(4) |
|
|
(5) |
If the operation period T
is divided into![]() intervals (with durations T1,
T2, …, TM) and each interval has a required
demand level (W1, W2, …, WM
, respectively), then the generalized MSS reliability index A is:
intervals (with durations T1,
T2, …, TM) and each interval has a required
demand level (W1, W2, …, WM
, respectively), then the generalized MSS reliability index A is:
|
|
(6) |
We denote by W and T
the vectors ![]() and
and ![]() (
(![]() ), respectively. As the
reliability A is a function of k1, k2, …, kn,
W and T. In the case of electrical power system, the vectors W
and T define the cumulative load curve (consumer demand). In general,
this curve is known for every power system.
), respectively. As the
reliability A is a function of k1, k2, …, kn,
W and T. In the case of electrical power system, the vectors W
and T define the cumulative load curve (consumer demand). In general,
this curve is known for every power system.
In the classical reliability, much work was devoted to the binary state reliability analysis, where the system is either working perfectly or completely failed. In this paper, the system and its devices are considered to have a range of performance levels, MSS reliability theory will be used. The most of research works in MSS reliability can be found in [11] or [12]. Generally speaking, the methods of MSS reliability assessment are based on four different approaches:
1. The structure function approach.
2. The stochastic process (Markov) approach.
3. The Monte-Carlo simulation technique.
4. The universal moment generating function (UMGF) technique.
In [11], a comparison between these four approaches highlights that the UMGF technique is fast enough to be used in the complex problems where the search space is sizeable.
Reliability estimation based on Ushakov's technique
The last few years have seen the appearance of a number of works presenting various methods of quantitative estimation of systems consisting of devices that have a range of working levels in [13] and [14]. In general forms the series connection, the level of working is determined by the worst state observed for any one of the devices, while for parallel connection is determined by the best state. However, such the approach is not applicable for the majority of real systems.
In this paper the procedure used is based on the universal z-transform, which is a modern mathematical technique introduced in [15]. This method, convenient for numerical implementation, is proved to be very effective for high dimension combinatorial problems. In the literature, the universal z-transform is also called UMGF or simply u-transform. The UMGF extends the widely known ordinary moment generating function [16]. The UMGF of a discrete random variable X is defined as a polynomial:
|
|
(7) |
Where the variable X has ![]() possible values and
possible values and ![]() is the
probability that X is
equal to Xj.
is the
probability that X is
equal to Xj.
The probabilistic characteristics of the random variable X can be found using the function u(z). In particular, if the discrete random variable X is the MSS stationary output performance, the availability A is given by the probability Proba(X ≥ W) which can be defined as follows:
|
Proba(X ≥ W) = Φ(u(z)z-W) |
(8) |
Where Φ (a distributive operator) is defined by expressions (9) and (10):
|
|
(9) |
|
|
(10) |
It can be easily shown that equations
(9)-(10) meet the condition: ![]() . By using the operator Φ,
the coefficients of polynomial u(z) are summed for every term with Xj ³ W, and the probability that X is not less than some arbitrary
value W is systematically obtained.
. By using the operator Φ,
the coefficients of polynomial u(z) are summed for every term with Xj ³ W, and the probability that X is not less than some arbitrary
value W is systematically obtained.
Consider single devices with total failures and each device i has nominal performance Xi and reliability Ai. The UMGF of such an element has only two terms can be defined as:
|
ui(z) = (1-Ai)z0 + AizXi = (1-Ai) + AizXi |
(11) |
To evaluate the MSS availability of a series-parallel system, two basic composition operators are introduced. These operators determine the polynomial u(z) for a group of devices.
Parallel devices
Let us consider a system device m containing Jm devices connected in parallel. The total performance of the parallel system is the sum of performances of all its devices. In power systems, the term capacity is usually used to indicate the quantitative performance measure of a device in [17]. The u-function of MSS device m containing Jm parallel devices can be calculated by using the Á operator:
|
up(z) = Á(ui(z), u2(z), …, un(z)) |
|
where ![]() .
.
Therefore for a pair of devices connected in parallel:
|
|
|
The parameters ai
and bj are physically interpreted as the performances of the
two devices. n and m are numbers of possible performance levels
for these devices. Pi and Qj are
steady-state probabilities of possible performance levels for devices. One can
see that the Á operator is
simply a product of the individual u-functions. Thus, the device UMGF
is: ![]() .
Given the individual UMGF of devices defined in equation (11), we have:
.
Given the individual UMGF of devices defined in equation (11), we have:
|
|
|
Series devices
When the devices are connected in series, the device with less performance becomes the bottleneck of the system. This device therefore defines the total system productivity. To calculate the u-function for system containing n devices connected in series, the operator δ should be used: us(z) = δ(u1(z), u2(z),…,um(z)), where δ(X1, X2, …,X3) = min{X1, X2, …, Xm}, so that:
|
|
|
Applying composition operators Á and δ consecutively, one can obtain the UMGF of the entire series-parallel system. To do this we must first determine the individual UMGF of each device.
Devices with total failures
Let’s consider the usual case where only total failures are considered and each subsystem of type i and version vi has nominal performance Xiv and availability Aiv. In this case, we have: Proba(X = Xiv) = Aiv and Proba(X = W) = 1-Aiv.
The UMGF of such an device has only two terms can be defined as in equation (11) by u*i(z) = (1-Aiv)z0 + AivzXiv = 1-Aiv + AivzXiv. Using the Á operator, we can obtain the UMGF of the i-th system device containing ki parallel devices: ui(z) = (u*i(z))ki = (AivzXiv + (1-Aiv))ki.
The UMGF of the entire system containing n devices connected in series is:
|
|
(12) |
To evaluate the probability Proba(X ≥W) for the entire system, the operator Φ is applied to equation (12):
|
Proba(X ≥W) = Φ(us(z)z-W) |
(13) |
The Ant Colony System Approach
Ant Colony Optimization (ACO) is one of the adaptive meta-heuristic optimization methods inspired by nature which include simulated annealing, genetic algorithms and tabu search. ACO is distinctly different from these methods in that it is a constructive, rather than an improvement, algorithm. ACO was inspired by the behaviour of real ants. Ethologists have studied how blind animals, such as ants, could establish shortest paths from their nest to food sources. The medium that is used to communicate information among individual ants regarding paths is pheromone trails. A moving ant lays some pheromone on the ground, thus marking the path. The pheromone, while gradually dissipating over time, is reinforced as other ants use the same trail. Therefore, efficient trails increase their pheromone level over time while poor ones reduce to null. Inspired by this behaviour of real ants, Marco Dorigo first introduced the ant colony optimization approach in his Ph.D. thesis in 1992 [17] and expanded it in his further work as summarized in [18, 19, 20, 2 1].
The general algorithm
To apply the ACO meta-heuristic to a combinatorial optimization problem, it is convenient to represent the problem by a graph G = (N, S), where N are the nodes and S is the set of edges. To represent our problem as such a graph, the set of nodes N is given by subsystem and components, and edges connect each subsystem to its available components. Some nodes are added to represent positions where additional component was not used. As in [19], these nodes are called blanks nodes and have attributes of zero. The obtained graph is partially connected. Ants cooperate by using indirect from of communication mediated by pheromone they deposit on the edges of the graph G while building solutions.
In fact, the algorithm works as follows: M ants are initially positioned on node representing a subsystem. Each ant looks for a solution and represents one possible topology of the entire system. This topology is represented by Ki devices put in parallel for n different components. The Ki devices can be chosen among any combination from Vi available type of components. Each ant builds a feasible solution (tour) to the reliability optimization problem. Applying this iteration becomes a stochastic rule. At each constructing solution, ant also modifies the amount of pheromone for each visited edges by local updating rule. When all ants finished their tour, a pheromone amount is modified again by global updating rule. A heuristic information (hij) and pheromone amount (tij) guide the ants to build the best solution to select Ki best reliabilities devices in each subsystem. At each node i an ant is positioned to choose the device j by applying the simple expression:
|
|
(14) |
And J is chosen according to the probability:
|
|
(15) |
where a =the relative importance of the trail; b = the relative importance of the heuristic information hij; ACi = the set of available reliable devices choices for subsystem i; q = random number uniformly generated between 0 and 1.
The heuristic information used is: hij=1/(1+Aij) where Aij represents the associated reliable of device j for subsystem i. A “tuning” factor ti= hij=1/(1+Ai(Mi+1)) is associated to blank device (Mi+1) of subsystem i. the reliable devices is arranged from the best one to the bed one. The parameter qo determines the relative importance of exploitation versus exploration: every time an ant in subsystem i have to choose a device j, it samples a random number 0 ≤ q ≤ 1. If q ≤ qo then the best edge, according to (14), is chosen (exploitation), otherwise an edge is chosen according to (15).
The local updating pheromone
While the ants built a solution of the reliability optimization problem, these ants choose reliable device by the visiting edges on the graph G, and their pheromone level is updated by local rule given by:
|
|
(16) |
Where r is a coefficient such that (1-r) represents the evaporation of trail and t0 is an initial value of trail intensity. It is initialized to the value(n.TAnn)-1 with n is the size of the problem (i.e. number of subsystem and total number of available devices) and TAnn is the result of a solution obtained through some simple heuristic.
The global updating pheromone
After all ants have built a complete configuration, pheromone is updated, only for the best ant. A amount of pheromone Dtij is deposited on each edge that the best ant has used. This amount is given by 1/TAnm-best where TAnm-best is the reliable device system design. Therefore, the global updating pheromone can be given as:
|
|
(17) |
Such as:
|
|
(18) |
The followings are formal description of the algorithm.
Set NC:=0 (NC: cycle counter)
For every edge (i,j) set an initial value tij(0)= to
1. For k=1 to NbAnt do
2. For i=1 to NbSubSystem do
For j=1 to MaxComponents do
Choose a component, including blanks, according to (14) and (15).
Local update of pheromone trail for chosen subsystem- component edge (i,j)0:
![]()
End For
End For
3. Calculate Rk (system reliability for each ant)
Calculate the total cost for each ant TCk
Update the best found feasible solution
4. Global update of pheromone trail:
For each edge (i,j)Î best feasible solution, update the pheromone trail according to:
![]()
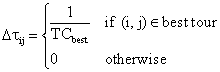
End For
5. cycle = cycle +1
6. if (NC < NCmax) and ( not stagnation behaviour)
Then
Go to step 2
Else
Print the best feasible solution and components selection.
Stop.
Illustrative Example
In order to illustrate the proposed ant colony algorithm, a numerical example is solved by use of the data given in tables 1. Table 1 shows the demands levels as a percentage of the maximum load.
Table 1. Parameters of the cumulative demand curve
|
Demand level (%) |
100 |
80 |
50 |
20 |
|
Duration (h) |
4203 |
788 |
1228 |
2536 |
Each element of the sub-system is considered as a unit with total failures. Table 2 contains the data of cumulative demand. Table 3 presents the obtained configuration.
Tables 2. Data examples
|
Sub # |
Devi # |
Avai A |
Cost C |
Per X |
|
|
Power Units |
1 |
1 2 3 4 5 6 7 |
0.980 0.977 0.982 0.978 0.983 0.992 0.984 |
0.590 0.535 0.470 0.42 0.40 0.18 0.22 |
120 100 85 85 48 31 26 |
|
HT Transformers |
2 |
1 2 3 4 5 |
0.995 0.996 0.997 0.997 0.998 |
0.205 0.189 0.091 0.056 0.042 |
100 92 53 28 21 |
|
HT lines |
3 |
1 2 3 4 |
0.971 0.973 0.971 0.976 |
0.985 0.885 0.872 0.158 |
100 60 40 20 |
|
HT/MT Transformers |
4 |
1 2 3 4 5 6 7 8 9 |
0.977 0.978 0.978 0.983 0.981 0.971 0.935 0.982 0.977 |
0.18 0.16 0.15 0.121 0.102 0.096 0.071 0.715 0.044 |
115 100 91 72 72 72 55 25 25 |
|
Comp #: System component number; Vers #: System version number |
|||||
Table 3. Computing Results
|
Constraint |
Optimal Topology |
|
||
|
Ad |
A |
C(MillionU€) |
||
|
0.97 |
Subsys 1 Subsys 2 Subsys 3 Subsys 4 |
6 4 7 1 3 6 5 5 1 4 2 3 2 4 3 4 6 9 2 5 8 7 3 1 4 |
0.9860 |
19.942 |
|
0.95 |
Subsys 1 Subsys 2 Subsys 3 Subsys 4 |
6 2 5 7 3 6 4 5 1 4 3 2 4 3 4 4 4 6 3 5 9 8 1 7 2 |
0.9502 |
17.252 |
Description of the system to be optimized
The electrical power station system which supplies the consumers is designed with four basic sub-systems (stations) as depicted in Figure 2. This figure showed the detailed process of the electrical power station system distribution.
The process of electrical power system distribution follows as: The electrical power is generated from the station units (component 1). Then transformed for high tension (HT) by the HT transformers (component 2) and carried by the HT lines (component 3). A second transformation in HT/MT transformers (component 4), which supplies the MT load (throw the MT lines). Each element of the system is considered as unit with total failures.
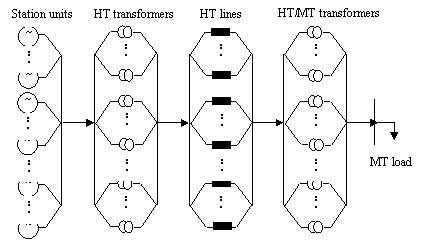
Figure 2. Detailed generating power station system
To provide a desired availability or reliability “t“ present time, the system should be expended by the choice among several products available on the market. The characteristics for each type of equipment are presented in Table 2.
This latter shown for each Device (Devi) availability A, nominal performance X and cost unit C. both the equipment performance (capacity) and the demand levels can be measured as a percentage of the maximum boiler capacity (Demand) at each stage. Interval duration of load can be measured as a fraction (percentages %) of the total operation time.
Results and Discussion
Table 3 illustrate the computation of two basic indices (cost and reliability) corresponding to their optimal or near optimal structure.
In order to show the effect of the desired availability on the investments cost. Two different values of Ad are considered.
The best system structures, obtained by the suggested approach for two desired reliability levels Ad (0.97 and 0.9), are determined by the number and the version of components in each subsystem
The solution depends strongly of ACS parameter choices. An experiment is implemented. In this experiment a set of values parameters of ACS algorithm are tested, the choice of these values affects strongly the solutions. The best values that show the best structure are: a = 5, b = 2, t0 = 0.05 and r = 0.008.
Conclusion
In conclusion, in this paper we have shown that the hybrid approach which combines between the UMGF and the ANT system is an interesting approach to solve the Redundancy Optimization Problem. This approach allows us to minimize the total investments cost subject to availability constraint.
This approach will be especially applicable to problems where an exact calculation of objective function is not possible. This situation is found in Redundancy Optimization Problem in complex and/or large Multi state Power Systems.
References
1. Dorigo M., Maniezzo V., Colorni A.. The Ant System: Optimization by a colony of cooperating agents, IEEE Transactions on Systems, Man and Cybernetics- Part B, 1996, 26(1), p. 1-13.
2. Dorigo M., Gambardella L. M., Ant Colony System: A Cooperative Learning Approach to the Traveling Salesman Problem, IEEE Transactions on Evolutionary computation, 1997, 1(1), p. 53-66.
3. Maniezzo V., Colorni A., The Ant System Applied to the Quadratic Assignment Problem, IEEE Transactions on Knowledge and data Engineering, 1999, 11(5), p. 769-778.
4. Bauer A., Bullnheimer B., Hartl R. F., Strauss C., Minimizing Total Tardiness on a Single machine using Ant Colony Optimization, Central European Journal of Operations Research, 2000, 8(2), p. 125-141.
5. Liang Y. C., Smith A. E., An Ant Colony Optimization Algorithm for the Redundancy Allocation Problem (RAP), IEEE Transactions on Reliability, 2004, 53(3), p. 417-423.
6. Bullnheimer B., Hartl R. F., Strauss C., Applying the Ant System to the vehicle Routing problem, The 2nd Metaheuristics International Conference (MIC-97), Sophia-Antipolis, France, 1997, p. 21-24.
7. Di Caro G., Dorigo M., Mobile Agents for Adaptive Routing, Proceedings for the 31st Hawaii International Conference On System Sciences, Big Island of Hawaii, 1998, p. 74-83.
8. Costa D., Hertz A., Ants Colour Graphs, Journal of the Operational Research Society, 1997, 48, p. 295-305.
9. Ross S. M., Introduction to probability models, Academic press, 1993.
10. Murchland B., Fundamental concepts and relations for reliability analysis of multi-state systems, In: Reliability and Fault Tree Analysis, ed. R. Barlow, J. Fussell, N. Singpurwalla, SIAM, Philadelphia, 1975.
11. Billinton R., Allan R., Reliability evaluation of power systems, Pitman, 1990.
12. Ushakov I. A., Levitin G., Lisnianski A., Multi-state system reliability: from theory to practice, Proc. of 3rd Int. Conf. on mathematical methods in reliability, MMR 2002, Trondheim, Norway, p. 635-638.
13. Levitin G., Lisnianski A., A new approach to solving problems of multi-state system reliability optimization, Quality and Reliability Engineering International, 2001, 47(2), p. 93-104.
14. Reinschki B., System of elements with many states, Radio isvyaz, Moscow, 1985.
15. EL-Neweihi E., Proschan F., Degradable systems: A survey of multi states system theory, Common. Statis. Theory Math., 1984, 13(4), p. 405-432.
16. Ushakov I. A., Universal generating function, Sov. J. Computing System Science, 1986, 24(5), p. 118-129.
17. Chern M. S., On the Computational Complexity of Reliability redundancy Allocation in a Series System, Operations Research Letters, 1992, 11, p. 309-315.
18. Dorigo M., Optimization, Learning and Natural Algorithms, Ph.D. Thesis, 1992, Politecnico di Milano, Italy.
19. Dorigo M., Di Caro G., The Ant Colony Optimization Meta-Heuristic, In: New Ideas in Optimization (Corne D., Dorigo M., Glover F., Eds.), McGraw-Hill, pp. 11-32, 1999.
20. Dorigo M., Di Caro G., Gambardella L. M., Ant Algorithms for Discrete Optimization, Artificial Life, 1999, 5(2), p. 137-172.
21. Dorigo M., Maniezzo V., Colorni A., Ant System: Optimization by a Colony of Cooperating Agents, IEEE Transactions on Systems, Man, and Cybernetics-Part B: Cybernetics, 1996, 26(1), p. 29-41.