Spreading of Trisiloxanes on Thin Water Film: Moving Front Profile
Derrick Ovunda NJOBUENWU1,2
1 Department of Chemical/Petrochemical Engineering, Rivers State University of Science & Technology, PMB 5080 Port Harcourt, Nigeria; 2 Institute of Particle Science & Engineering, School of Process, Environmental & Materials Engineering, University of Leeds, Leeds LS2 9JT United Kingdom
donadviser@yahoo.co.uk, Chedon@leeds.ac.uk
Abstract
The spreading of aqueous drops of surfactant on the surface of thin water film was recorded using an Olympus high speed video system with a speed of 100 frames per second. The surfactants used were trisiloxanes of polyethylene oxide chain length between 6 and 9 (EO6-EO9). The results showed that the spreading of trisiloxanes (EO6, EO7, EO8 and EO9) at concentration above their critical micelle concentration, CMC on a thin water surface of 320 microns film thickness involved two stages and was completed within few seconds. The images of the spreading of the surfactants show the development of a thickened front that spreads in the direction of uncontaminated interface. Upstream of the front, there exists a thinned region and the remnants of the drop that looks like a depressed cap. The initial stage of the spreading has a high power law exponent between 0.42 and 0.63; this is followed by a second stage characterised by a lower power law exponent between 0.28-0.35. The second stage was accompanied by the formation of dry spot at the centre of the Petri dish.
Keywords
Marangoni Effect, Thin Liquid film, Spreading Kinetics, Superspreading, Trisiloxanes
Introduction
Trisiloxane surfactants have been recognized as effective wetting agents for water-based herbicides on waxy plant leaves (Zabkiewicz and Gaskin, 1989). The trisiloxane shown in Figure 1 is denoted as M(D’EOnR)M, where M represents the trimethylsiloxy group (CH3)3SiO; D’ = -SiCH3R’; R’= (CH2)3; EOn = polyethylene oxide group (OCH2CH2)n; n = average number of the polyethylene oxide group 3,4, 5 …. The chain length is a measure of the surfactant’s degree of hydrophilicity. R stands for an end-capping group, usually -H, -CH3, or -Ac; Ac = -C(O)CH3.

Figure 1. Molecular structure of the trisiloxane surfactants M(D′EnOH)M
They reduce the contact angle of water on a large variety of low- and high-energy surfaces, and cause rapid and complete (or nearly complete) spreading (termed superspreading). Superspreading is an unusually rapid spreading of a dilute (about 0.1 wt %) aqueous dispersion of the surfactant over a hydrophobic surface such as paraffin wax film or waxy leaf surfaces (Zhu et al., 1994).
The relation of the striking spreading behaviour, the surfactant nature, the phase behaviour, and the surface tension dynamics has received extensive investigation in the scientific literature in recent years (Stoebe et al., 1996, 1997a, b; c; Svitova et al., 2001; Chengara et al., 2002; Nikolov et al., 2002). The main findings in silicone surfactants (Hill, 2002) and superspreading of trisiloxanes (Hill, 1998a) have been reviewed by Hill.
Spreading of surfactant over the surface of thin liquid layers receives considerable attention in both the theoretical and experimental literature (Hill, 1998b). Such spreading processes are of importance to numerous industrial, biomedical and daily life settings, including coating flow technology, micro-fluidics, surfactant replacement therapy for neonates, film drainage in emulsions and foams and drying of semi-conductor wafers in microelectronics (Borgas and Grotberg, 1988; Matar and Craster 2001). A fluid flow is primarily driven by surface tension gradients that arise due to non-uniformities in the surfactant interfacial concentration, that, in turn, give rise to Marangoni stresses. These stresses drive rapid surfactant spreading in the direction of the uncontaminated (surfactant-free) liquid. Based on the principle of Marangoni flow, Starov et al. (1997) reported results of a theoretical and experimental study of the spreading of sodium dodecyl sulfate, SDS surfactant over a thin liquid layer with initial concentrations of SDS above critical micelle concentration, CMC. Two distinct stages of spreading at CMC with varying power law R(t) ~ tn were observed; the first stage was the faster, and it was connected with micelle dissolution with n » 0.60; the second stage was the slower, when the surfactant concentration fell below CMC with the formation of a dry spot in the centre the film given n » 0.25.
To our knowledge, spreading experiments involving trisiloxanes on thin water surface have not been previously reported in the literature. In this part one of the paper, the moving front illustrating the superspreading of trisiloxanes on thin water film is reported, while part two will focus of the dry spot profile of the surfactant in thin water. The experiments were done using an advanced video technique at 100 frames per seconds with a resolution of 800 ´ 600 pixels. This investigation was carried out to find the relation between surface tension driven spreading (Marangoni flow) and wetting behaviours of the trisiloxane surfactants showing superspreading ability, at trisiloxanes’ concentration above CMC. The experiments were performed at a concentration of 0.16% wt/wt, which corresponds to the maximum rate of spreading of trisiloxane EO8 solution (Zhu et al., 1994; Churaev et al., 2001)
Materials and Methods
Materials
Substrates:The liquid substrate was ultra-pure
water obtained from a Millipore Ultra Pure water System (Milli-Q plus 185,
Millipore Co., Bedford, WA) with a resistivity of ![]() and a
surface tension of 72.2 mN/m at 25°C. The glassware and syringes were cleaned
by successive rinses with concentrated H2SO4 - K2Cr2O7
and ultra water. The ultra pure water was also used in preparing the surfactant
solutions. Sterile circular borosilicate Petri dishes of diameter 15 cm
purchased from Fisher Scientific were used as the solid substrate on which the
thin liquid film was formed. This was positioned in a tripod adjustable ring.
This entire system rested on an anti-vibration table to reduce vibrations to a
tolerable minimum.
and a
surface tension of 72.2 mN/m at 25°C. The glassware and syringes were cleaned
by successive rinses with concentrated H2SO4 - K2Cr2O7
and ultra water. The ultra pure water was also used in preparing the surfactant
solutions. Sterile circular borosilicate Petri dishes of diameter 15 cm
purchased from Fisher Scientific were used as the solid substrate on which the
thin liquid film was formed. This was positioned in a tripod adjustable ring.
This entire system rested on an anti-vibration table to reduce vibrations to a
tolerable minimum.
Trisiloxanes: The trisiloxane surfactants were used as obtained from Dow Corning Co., Midland, MI, USA without further purification. The polyethylene oxide (EO) tails of the trisiloxane compounds are monodisperse, and the number given represents only the average tail length. Trisiloxanes of polyethylene oxide chain length 6 to 9 (represented as EO6 to EO9) were used in the experiment. Svitova et al. (1996) reported that the CMC for most non-ionic surfactants is usually about 0.01% (wt/wt) and is equal to 0.007% wt/wt (1.24 ´ 10-4 mol/kg) for EO8 and increases from 7 ´ 10-5 M to 5 ´ 10-4 M for ethoxylated isododecyl alcohols with an increase in the ethoxy chain length from 5 to 15. The density, ρ of pure EO8 at room temperature is 1.007 g /cm3, the viscosity, μ is 21 cP, and the solubility limit is 0.007 wt % (Lin et al., 1994). EO6 and EO8 form vesicles at the critical aggregation concentration (CAC) while EO12 forms micelles. The physical characteristics of trisiloxane surfactants solution are scanty but could be found in literatures in the references (Lin et al., 1994; Svitova et al., 1998; Rafai et al., 2002).
Method
The aqueous solutions and dispersions at a concentration 0.16 wt/wt % above CMC were prepared using 18.2 MΩcm Milli-Q reagent water. The concentration was measured in weight percent. The mixtures were hand shaken vigorously to disperse the surfactant and were allowed to stand for a reasonable time frame so that any foam formed by agitation had dissipated before the experiments were performed. Only relatively fresh (less than 2 days old) surfactant solutions were investigated to avoid hydrolysis and decrease in surface activity.
The experimental set as shown in Figure 2 consists of an Olympus High-speed camera, 1, connected to a personal computer, 2, for image storage and processing. The setup was illuminated from above and bottom using adjustable light source, 3, with a screen, 4, placed under the glass borosilicate Petri dish, 5; a micro-litre syringe, 6, to measure drop of surfactant solution and glass borosilicate Petri dish on which thin film of the liquid substrate, 7 is formed. The thin layer of liquid is prepared by coating the bottom of the borosilicate glass Petri dish of diameter 150 mm with 5.7 ml of ultra pure water measured with glass pipette. The resulting thickness was 0.32 ± 0.02 mm. The thickness of the thin film of the ultra pure water formed was determined by weight method. Dried empty Petri dish was weighed. The ultra pure water was added and the thickness was calculated using density of water and volume of a cylinder relationship. The experimental conditions correspond to 22 ± 2°C and a relative humidity of 40 ± 5%.
The spreading experiments were conducted by producing 3 μl drop of surfactants solution, 8, from the syringe such that it hung from the tip of the needle. The apex of the drop was then gently placed on the surface of the water film formed on borosilicate Petri dish (to avoid turbulence and external disturbances on the surface of the thin water film). On touching the water film surface, the surfactant solution spreads on it by Marangoni stresses and this motion is made visible using a small amount of talc powder as a marker. The expanding drop was viewed in transmitted light and captured using the Olympus High speed camera at the rate of 100 frames/sec. The frames were analysed using the camera’s associated software to get the radius of spread as function of time.
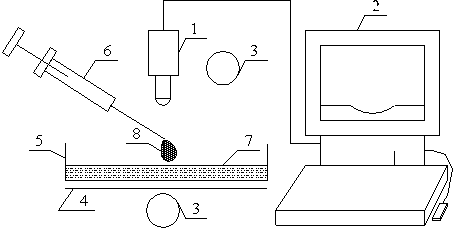
Figure 2. Schematic representation of the spreading of Surfactant Solution on thin water film in a Petri dish. 1 = Olympus high speed camera; 2 = Personal Computer; 3 = liquid source; 4 = optical screen; 5 = Borosilicate Petri dish; 6 = micro-litre syringe; 7 = thin water film; 8 = liquid droplet
After each measurement, the Petri dishes were immerse in concentrated H2SO4-K2Cr2O7 solution for about three hours at room temperature, then thoroughly rinsed with deionised water and ultra pure water, and is subsequently dried in vacuum oven at 70°C for about 30 minutes. The cleaning process is to remove any adsorbed surfactant, impurities and talc on the surface of the Petri dish. This will also prevent de-wetting of the thin liquid film layer during the experiment. Each spreading measurement was done three to five times until the reproducibility was satisfactory to ensure minimal relative error. The spreading area is the average of the areas obtained in each set of measurements
Results and Discussion
When a drop of aqueous trisiloxane solution was placed on the water layer, surface deformations are apparent almost immediately. This was similar to SDS on water film (Starov et al., 1997). On touching the water surface, the surfactant solution created surface tension gradient causing surface tension driven spreading. The fluid interface was then stretched by Marangoni force, causing the surfactant solution to move towards the region of low surfactant concentration and decreasing the concentration gradient. The distance travelled by the moving front of the expanding layer at time t is R(t). This distance was measured by sprinkling talc particles on the clean thin film surface. The talc particles are pushed away by the expanding monolayer. Typical frames grabbed for EO8 are shown in Figure 3. The images showing the evolution of the spreading surfactant with time for EO8 shown in Figure 3 are similar to the images observed with trisiloxanes EO6, EO7, and EO9 hence, the images are not repeated here to avoid redundancy of figure. Soon after deposition, a light central region is visible which corresponds to the spreading cap of surfactant, whereas the outer dark circle is the thickened rim. The edge of the inner circle is due to the curvature of the cap. The thickened front continues to advance uniformly with time. This profile attributes Marangoni phenomenon as the dominant force responsible for the initial spontaneous spreading and the evolution of dry spot at the centre of the Petri dish (Starov et al., 1997; Afsar-Siddiqui, et al. 2003a, 2003b, 2003c).
The Marangoni effect produced the initial fast stage of spreading (superspreading) with a very high power law exponent n ranging from 0.42 to 0.63. For the trisiloxanes investigated. The decrease in the concentration gradient retards the spreading leading to the second stage of slower spreading with power law exponent between 0.28 and 0.35.
|
0 sec, Frame 0, before the drop touches the film |
0.01 sec, Frame 0001, at the onset of spreading |
0.05 sec, Frame 0005 |
|
|
|
|
|
0.1 sec, Frame 0010 |
2.0 sec, Frame 0200 |
5.0 sec, Frame 0500 |
|
|
|
|
|
8.0 sec, Frame 0800 |
12 sec, Frame 1200 |
16 sec, Frame 1600 |
|
|
|
|
|
20 sec, Frame 2000 |
25 sec, Frame 2500 |
30 sec, Frame 3000 |
|
|
|
|
|
45 sec, Frame 4500 |
50 sec, Frame 5000 |
|
|
|
|
|
Figure3. Frames showing 3 μl drop of 0.16 wt/wt % EO8 solution deposited on a 0.32 mm thick water film; showing the spreading of the moving front and surface deformations, ripples, and dry spot phenomena due to Marangoni stresses developed. The frames were grabbed at 100 frames/sec using Olympus High speed camera
As the surface is stretched, the thin water film below was dragged along, causing an unsteady flow, which resulted in strong water film-surface deformation. This deformation was seen as waves and dry spot on the Petri dish. The strength of the Marangoni stresses is proportional to the surface tension gradient and the thickness of the underlying water film.
The spreading coefficients for the four trisiloxane solutions EO6, EO7, EO8 and EO9 used in the experiments were not determined; however, all the solutions spread spontaneously at the thin water surface due to anticipated initial positive spreading coefficient SLS = γSV - (γLV + γLS) = γSV – γLV – γLS where γSV, γLV, and γLS represent the substrate-vapour, liquid-vapour and liquid-substrate interfacial tensions respectively; liquid represents the trisiloxanes and substrate represents the thin water film.
The experimental results of moving front of surfactant solution spreading on the surface of thin ultra pure water are shown in Figures 5 to 8. Two stages of spreading were observed for the four trisiloxanes used. An initial fast stage of spreading called superspreading, followed by a slow stage of spreading. In general, good reproducibility of the spreading kinetics was observed for all of the hydrophilicity examined, particularly for the two stages of the spreading of the moving fronts, that is, the experimental error was within accepted limit.
Experimental data for the entire spreading process, from the moment when the surfactant drop was placed on the water surface to the final moment of observation (final stage of the spreading assumed was when the dry spot has reached the edge of the Petri dish) can be described by an n-power law relation as follows: R(t) ~ tn; where R(t) is the radius of the spreading of trisiloxane droplets on thin water film; and t is the time of spreading and n is power exponent that characterise the extent of spreading and are listed in Table 1. The values of exponent n and pre-exponential constant were calculated from experimental data of trisiloxane solutions spreading on ultra pure water using power regression analysis and presented as average ± standard deviation.
Table 1. Kinetics parameter of the two stages of the moving front of trisiloxanes.
|
Trisiloxanes |
Fist Stage Spreading |
Second Stage Spreading |
||||
|
n |
constant |
R2* |
n |
Constant |
R2* |
|
|
EO6 |
0.60 ± 0.02 |
26.71 ± 0.82 |
0.9663 |
0.28 ± 0.03 |
7.65 ± 0.22 |
0.9915 |
|
EO7 |
0.54 ± 0.00 |
9.96 ± 0.04 |
0.9977 |
0.35 ± 0.003 |
7.00 ± 0.10 |
0.9864 |
|
EO8 |
0.63 ± 0.03 |
11.98 ± 0.85 |
0.9779 |
0.34 ± 0.003 |
6.42 ± 0.11 |
0.9926 |
|
EO9 |
0.42 ± 0.004 |
6.77 ± 0.24 |
0.9948 |
0.31 ± 0.02 |
5.48 ± 0.02 |
0.9971 |
It is interesting to note that the spreading of trisiloxane solution with polyethylene chain length of eight (EO8) was faster than EO6, EO7 and EO9. EO9 spread slower than others, in spite of the fact that it has a greater degree of hydrophilcity (see Table 1). We do not have a clear explanation for this behaviour of EO9. However, Maldarelli and collaborators has posted that the superspreading ability of trisiloxanes decreases considerably for trisiloxanes with larger than eight polyethylene chain length. Hence, we infer that EO6, EO7 and EO8 are superspreaders with EO8 having greater ability for superspreading. Most work on super spreading of trisiloxanes on very hydrophobic solid substrates used EO8 (Zhu et al., 1994; Stoebe et al., 1996, 1997a, 1997b; Kumar et al., 1999; Churaev et al., 2001a and other ref in the literature review).
As shown in Figure 4, Figure 5, Figure 6 and Figure 7, the experimental data fit well to a power relationship in a log-log plot. The research did not establish the transition point from the first stage of fast spreading to the second stage of slow spreading. Jensen and Grotberg, 1992 predicted that the radius of a surfactant monolayer, driven by Marangoni convection with negligible gravitational and diffusion effects, progresses in time as t1/4. The exponents (n) of the first stage in Table 1 show values which are larger than 1/4, thus strongly suggesting that Marangoni convection is the main driving force for the spreading at the film thicknesses and surfactant concentrations used.
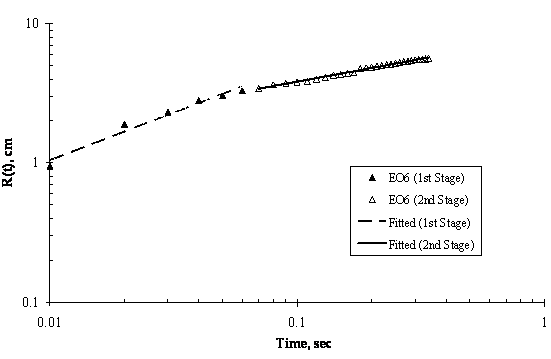
Figure 4. Log-Log Plot showing Moving Front Profile for 3μl drop of EO6 spreading on thin water film of thickness 0.32mm

Figure 5. Log-Log Plot showing Moving Front Profile for 3μl drop of EO7 spreading on thin water film of thickness 0.32mm
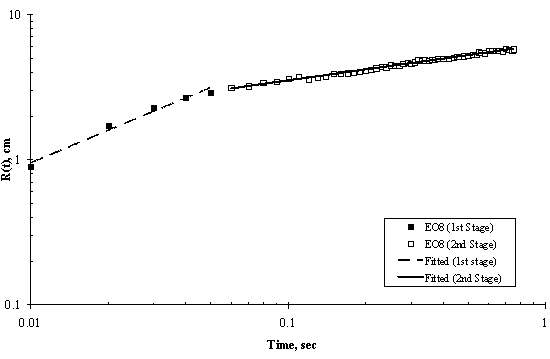
Figure 6. Log-Log Plot showing Moving Front Profile for 3μl drop of EO8 spreading on thin water film of thickness 0.32 mm

Figure 7. Log-Log Plot showing Moving Front Profile for 3μl drop of EO9 spreading on thin water film of thickness 0.32 mm
Conclusion
Using high-speed videography, the spreading of trisiloxanes at concentrations above their CMC was estimated. Two stages of spreading were observed. This observation suggests that the first stage of spreading of trisiloxanes drops on a thin water surface is a very spontaneous process and it is attributed to surface tension gradient otherwise called Marangoni effect. This is when the surfactant concentration is determined by the dissolution of micelles, with a duration fixed by the initial amount of micelles. The decrease in the concentration gradient retards the spreading leading to the second stage of slower spreading, which occurs simultaneously with dry spot. It was found that the n-power dependence governs the rate of spreading of the surfactant droplet on thin water film as a function of time, R(t) ~ tn. The exponent for the first stage of spreading for trisiloxanes EO6, EO7, EO8 and EO9 are 0.60, 0.54, 0.63 and 0.42 respectively. This means only EO9 does not have the superspreading characteristics.
Acknowledgement
The author is grateful to Dr. Randal M. Hill of Dow corning USA for supplying the trisiloxanes and to Professor Victor M. Starov and Ms Polina Prokopovich both of Loughborough University, UK for their fruitful discussion on the study.
References
1. Afsar-Siddiqui A. B., Luckham P. F., Matar O. K., (2003a), The spreading of Surfactant Solutions on Thin Liquid Films, Adv. Colloid and Interface Sci., 2003, 106, p. 183-236.
2. Afsar-Siddiqui A. B., Luckham P. F., Matar O. K., (2003b), Unstable Spreading of Aqueous Anionic Surfactant Solutions on Liquid Films. Part 1. Sparingly Soluble Surfactant, Langmuir, 2003, 19(3), p. 696-702.
3. Afsar-Siddiqui A. B., Luckham P. F., Matar O. K., (2003c), Unstable Spreading of Aqueous Anionic Surfactant Solutions on Liquid Films. 2. Highly Soluble Surfactant, Langmuir, 2003, 19(3), p. 703-708.
4. Borgas M. S., Grotberg J. B., Monolayer Flow on a Thin Film (Lung Application), J. Fluid Mech. 1988, 193, p. 151-170.
5. Chengara A., Nikolov A., Wasan D., Surface Tension Gradient Driven Spreading of Trisiloxane Surfactant Solution on Hydrophobic Solid, Colloids and Surfaces A: Physicochemical and Eng Aspects, 2002, 206(1-3), p. 31-39.
6. Churaev N. V., Esipova N. E., Hill R. M., Sobolev V. D, Starov V. M., Zorin Z. M., The Superspreading Effect of Trisiloxane Surfactant Solutions, Langmuir, 2001, 17(5), p. 1338-1348.
7. Hill R. M., (1998a), Superspreading, Current Opinion in Colloid and Interface Science, 1998, 3(3), p. 247-254.
8. Hill R. M., (1998b), Dynamics of Surfactant Enhanced Spreading, ECJ European Coatings Journal, 1998, 7-8, p. 550-553.
9. Hill R. M., Silicone Surfactants – New Developments, Current Opinion in Colloid & Interface Science, 2002, 7(5-6), p. 255-261.
10. Lin Z., Hill R. M., Davis H. T., Ward M. D., Determination of Wetting Velocities of Surfactant Superspreaders with the Quartz Crystal Microbalance, Langmuir, 1994, 10, p. 4060-4068.
11. Maldarelli C., Using Surfactants to Enhance Thermocapillary Migration of Bubbles and Drops and Facilitate Drop Spreading on Hydrophobic Surfaces (Unpublished Progress Report).
12. Matar O. K., Craster R. V., Models for Marangoni drying, Physics of Fluids, 2001, 13, p. 1869-1883.
13. Nikolov A. D., Wasan D. T., Chengara A., Koczo K., Policello G. A., Kolossvary I., Superspreading Driven by Marangoni Flow, Adv. in Colloid and Interface Sci., 2002, 96(1-3), p. 325-338.
14. Rafai S., Sarker D., Bergeron V., Meunier J., Bonn D., Superspreading: Aqueous Surfactant Drops Spreading on Hydrophobic Surfaces, Langmuir, 2002, 18(26), p. 10486-10488.
15. Starov V. M., de Ryck A., Velarde M. G., On the Spreading of an Insoluble Surfactant over a Thin Viscous Liquid Layer, J. Colloid Interface Sci., 1997, 190(1), p. 104-113.
16. Stoebe T., Hill R. M., Ward M. D., Davis H. T., (1997a), Enhanced Spreading of Aqueous Films Containing Ionic Surfactants on Solid Substrates, Langmuir, 1997, 13, p. 7276-7281.
17. Stoebe T., Lin Z., Hill R. M., Ward M. D., Davis H. T., (1997b), Enhanced Spreading of Aqueous Films Containing Ethoxylated Alcohol Surfactants on Solid Substrates, Langmuir, 1997, 13, p. 7270-7275.
18. Stoebe T., Lin Z., Hill R. M., Ward M. D., Davis H. T., (1997c), Superspreading of Aqueous Films Containing Trisiloxane Surfactant on Mineral Oil, Langmuir, 1997, 13, p. 7282-7286.
19. Stoebe T., Lin Z., Hill R. M., Ward M. D., Davis H. T., Surfactant-Enhanced Spreading, Langmuir, 1996, 12, p. 337-344.
20. Svitova T. F., Hill R. M., Radke C. J., Spreading of Aqueous Trisiloxane Surfactant Solutions over Liquid Hydrophobic Substrates, Langmuir, 2001, 17(2), p. 335-348.
21. Svitova T. F., Hoffmann H., Hill R. M., Trisiloxane Surfactants: Surface/Interfacial Tension Dynamics and Spreading on Hydrophobic Surfaces, Langmuir, 1996, 12, p. 1712-1721.
22. Svitova T., Hill R. M., Smirnova Yu., Stuermer A., Yakubov G., Wetting and Interfacial Transitions in Dilute Solutions of Trisiloxane Surfactants, Langmuir, 1998, 14(18), p. 5023-5031.
23. Zabkiewicz J. A., Gaskin R. E., Effect of Adjuvants on Uptake and Translocation of Glyphosate in Gorse, Adjuvants Agrochem., 1989, 1, p. 141-149.
24. Zhu X., Miller W., Scriven L., Davis H., Superspreading of Water-Silicone Surfactant on Hydrophobic Surfaces, Colloids Surf. A, 1994, 90, p. 63-78.
Nomenclature
Symbols: n = exponents; R(t)
= radius of the drop base; S = spreading coefficient; ![]() = time
= time
Greek: μ =dynamic viscosity of the liquid; ρ = liquid density; γLS = liquid-substrate interfacial tension; γLV = liquid-vapour interfacial tension; γSV = substrate-vapour interfacial tension
Subscripts: L = liquid; V = vapour; S = substrate.
Acronyms: CAC = critical aggregation concentration; CCD = Charged-Coupled Device Camera; CMC = Critical Micelle Concentration; EO = Polyethylene Oxide; EO6 = Trisiloxane with Six Polyethylene Oxide chain length; EO7 = Trisiloxane with Seven Polyethylene Oxide chain length; EO8 = Trisiloxane with eight Polyethylene Oxide chain length; EO9 = Trisiloxane with nine Polyethylene Oxide chain length.













