Spreading of Trisiloxanes on Thin Water Film: Dry Spot Profile
Derrick Ovunda NJOBUENWU
Institute of Particle Science & Engineering, School of Process, Environmental & Materials Engineering, University of Leeds, Leeds LS2 9JT United Kingdom
donadviser@yahoo.co.uk, chedon@leeds.ac.uk
Abstract
This paper reports the results of an experimental investigation of the spreading of trisiloxanes EO6, EO7, EO8, EO9 and sodium dodecyl sulphate SDS on thin films which are 320 microns in thickness; the concentrations covered are above the CMC. The spreading of SDS is accompanied by the formation of a “dry spot” which advances in time roughly as t1/4. The trisiloxanes spreading gave rise to dry spot formation that was accompanied by “irregularities”, which corresponded to an abrupt jump in the plot of dry spot radius versus time. The behaviour is attributed to a variety of factors: disjoining pressure effects or the fact that the Petri dish was too small so that backward propagating waves were set up due to reflections from the walls which interacted with the outspreading dry spot.
Keywords
Marangoni Effect; Thin Film; Spreading; Trisiloxanes; Sodium Dodecyl Sulphate; Dewetting; Dry spot
Introduction
Spreading of one liquid over another is of a significant process that occurs in many interesting and important physical processes, with applications in various fields such as coating flow technology, micro-fluidics, surfactant replacement therapy for neonates, film drainage in emulsions and foams and drying of semi-conductor wafers in microelectronics. The spreading process has been identified to be strongly influenced by the surface tension of the liquid interfaces and the physics of the triple junction, where the three phases (vapour/liquid/liquid) intersect [1,2]. Figure 1 is the schematic diagram showing the spreading of liquid on another liquid surface.
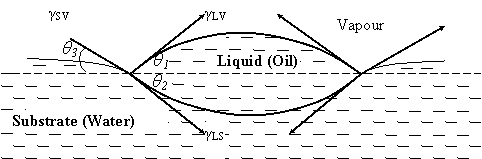
Figure 1. Diagrammatic representation of a drop of oil remaining as a lens on the surface of water; where γSV, γ LV, and γ LS represent the substrate-vapour, liquid-vapour and liquid-substrate interfacial tensions respectively; liquid represents the oil and substrate represents the water
Resolving the surface tension forces and equating the horizontal components of the tensions yields γSV cosθ3 = γLV cos θ1 + γLS cos θ2. As γLV, and γLS exert their full effect to balance γSV, θ1, θ2, and θ3 will tend to zero, and γSV > γLV + γLS. Harkins [3] used this to define an initial spreading coefficient, SLS of a liquid, L on substrate, S which is the difference between the free energy of the uncovered and the liquid covered regions of the substrate as SLS = γSV – (γLV + γLS) = γSV – γLV + γLS.
Experimental investigation of the spreading of trisiloxanes on thin films which are 320 microns in thickness; the concentrations covered are above the CMC.
The spreading of drops of sodium dodecyl sulfate (SDS) and trisiloxanes of polyethylene oxide chain length between six and nine (EO6 – EO9) on thin water film which is 320 microns in thickness were investigated to understand the spreading of liquid on another liquid. The trisiloxane surfactants have the ability of inducing wetting and have been shown to give rise to the so-called superspreading phenomenon whereby the spreading of droplets of dilute concentrations of this surfactant on a low energy surface takes place rapidly and with an unusually high spreading exponent. This is then followed by a second, slower spreading stage. The moving front profile, wetting properties and reviews on previous works on the spreading of Trisiloxanes on substrates are presented in the first part of this work [4].
Surface active agents deposited on the surface of a stable film will give rise to Marangoni stresses that cause local thinning. This may be severe enough to allow intermolecular forces to cause rupture of the film [5]. Kheshgi and Scriven [6] demonstrated this by placing a 5 ml drop of methanol on a 0.4 mm glycerine/water film on a glass plate. The methanol lowers the surface tension locally and fluid is drawn away from the deposited region by Marangoni stresses. Further downstream, an elevated rim is formed 4 sec later rupture occurs. The rupture creates a dry patch, which grows as liquid moves away from it and accumulates into a rim, the width and height of which increases with time are shown in Figure 2. The native film ahead of the rim is motionless as verified by the use of talc particles [7,8]. The radius of the dewetting hole, RD(t), grows linearly with time, while the width of the rim, Rw(t), advances with time as t1/2 [9,10].
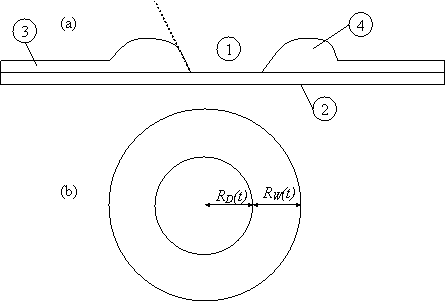
Figure 2. Schematic diagram of a dewetting hole; (a) a side view and (b) a top view. RD(t) is the radius of the dewetting hole and RW(t) is the width of the rim. 1- dry spot, 2- solid substrate(Petri dish), 3- dewetting film, 4- rim
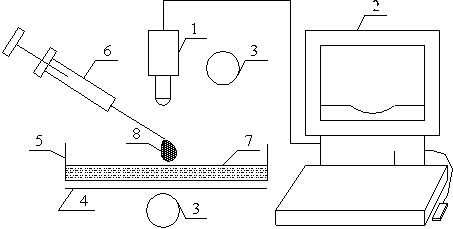
Figure 3. Schematic representation of the spreading of Surfactant Solution on thin water film in a Petri dish. 1, Olympus high speed camera; 2, Personal Computer; 3, liquid source; 4, optical screen; 5, Borosilicate Petri dish; 6, micro-litre syringe; 7 thin water film; 8, liquid droplet
This second part of the research focuses of the dry spot profile of the SDS and trisiloxanes surfactants at a concentration above critical micelle concentration (CMC) on thin water. The experiment was done with care using a high speed camera in which the images were captured at 100 frames per seconds with a resolution of 800×600 pixels. The concentration of trisiloxanes used was 0.16% wt/wt, which corresponds to the maximum rate of spreading of trisiloxane EO8 solution [11,12] and that of SDS was 20 g/l.
Materials and Methods
Materials
Substrates: Ultra-pure water with a resistivity of 18.2MΩcm and a surface tension of 72.2 mN/m at 25°C was used as the liquid substrate as obtained from a Millipore Ultra Pure water System. The distilled water was used to clean the glassware and syringes and to prepare the surfactant solution. The thin water film was formed on sterile circular borosilicate Petri dishes of diameter 15 cm obtained from Fisher Scientific.
Sodium Dodecyl Sulfate (SDS): Aqueous solutions of anionic sodium dodecyl sulfate (SDS) from Merck at a concentration c = 20 g/ l, above critical micellar concentration, CMC was used. The CMC of SDS is 4 g/l [13]. The physical characteristics of the SDS solution are molecular weight 288.4 g/mole; Surface tension at CMC is 38.3 ±1 mN/m [14].
Trisiloxanes: The trisiloxane surfactants were used as obtained from Dow Corning Co., Midland, MI, USA without further purification. The polyethylene oxide (EO) tails of the trisiloxane compounds are monodisperse, and the number given represents only the average tail length. Trisiloxanes of polyethylene oxide chain length 6 to 9 (represented as EO6 to EO9) were used in the experiment. The aqueous solutions and dispersions at a concentration 0.16 wt/wt % above CMC were prepared using 18.2MΩcm Milli-Q reagent water. The choice of the concentration is explained in [4]. The concentration was measured in weight percent. The mixtures were hand shaken vigorously to disperse the surfactant and were allowed to stand for a reasonable time frame so that any foam formed by agitation had dissipated before the experiments were performed. Only relatively fresh (less than 2 days old) surfactant solutions were investigated to avoid hydrolysis and decrease in surface activity.
Method
The experimental setup as shown in Figure 3 consists of an Olympus High-speed camera, 1, connected to a personal computer, 2, for image storage and processing. The setup was illuminated from above and bottom using adjustable light source, 3, with a screen, 4, placed under the glass borosilicate Petri dish, 5; a micro-litre syringe, 6, to measure drop of surfactant solution and glass borosilicate Petri dish on which thin film of the liquid substrate, 7 is formed. The thin layer of liquid is prepared by coating the bottom of the borosilicate glass Petri dish of diameter 150 mm with 5.7ml of ultra pure water measured with glass pipette. The resulting thickness was 320 microns. The thickness of the thin film of the ultra pure water formed was determined by weight method. Dried empty Petri dish was weighed. The ultra pure water was added and the thickness was calculated using density of water and volume of a cylinder relationship. The experimental conditions correspond to 22 ± 2°C and a relative humidity of 40 ± 5°C.
The spreading experiments were conducted by producing 3μl drop of surfactants solution, 8, from the syringe such that it hung from the tip of the needle. The apex of the drop was then gently placed on the surface of the water film formed on borosilicate Petri dish (to avoid turbulence and external disturbances on the surface of the thin water film). On touching the water film surface, the surfactant solution spreads on it by Marangoni stresses and this motion is made visible using a small amount of talc powder as a marker. The expanding drop was viewed in transmitted light and captured using the Olympus High speed camera at the rate of 100 frames/sec. The frames were analysed using the camera’s associated software to get the radius of spread as function of time.
After each measurement, the Petri dishes were immerse in concentrated H2SO4-K2Cr2O7 solution for about three hours at room temperature, then thoroughly rinsed with deionised water and ultra pure water, and is subsequently dried in vacuum oven at 70oC for about 30 minutes. The cleaning process is to remove any adsorbed surfactant, impurities and talc on the surface of the Petri dish. This will also prevent de-wetting of the thin liquid film layer during the experiment. Each spreading measurement was done three to five times until the reproducibility was satisfactory to ensure minimal relative error. The spreading area is the average of the areas obtained in each set of measurements.
Results and Discussion
As reported in part one of these researches [4], on touching the water surface, the surfactant solution created surface tension gradient causing surface tension driven spreading. The fluid interface was then stretched by Marangoni force, causing the surfactant solution to move towards the region of low surfactant concentration and decreasing the concentration gradient. The distance travelled by the moving front of the expanding layer at time t is R(t). Simultaneously as the surfactant was spreading the experimental profile revealed an almost immediate rupture of the water film, followed by dry spot at the centre and subsequent expansion of same with time. The formation and expansion of dry spot has been known to occur in spreading experiments on thin liquid substrates [13,15,16]
As the surface of the thin water film is stretched, the fluid below is dragged along, causing an unsteady flow, which resulted in strong fluid-surface deformation. Due to the created surface tension gradient, the liquid starts to flow away from the spot of introduction of surfactant solution creating a hole referred to herein as dry spot, but referred to as dewetting in some literature. The dry spot also progressed with time and the power law, RD(t) ~ tn with respect to time was determined. The kinetics of the dry spot phenomena for five different experiments on SDS obtained from Figure 4 are shown in Table 1, with a mean value of the power law exponent as 0.25 with standard deviation of 0.01. Therefore, the spreading kinetics for the dry spot phenomena for SDS obeying power law is RD(t) ~ t0.25±0.01. This is in good agreement with the work of Starov et al. [13]

Figure 4. Dry Spot Profile for 3μl drop of SDS spreading on thin water film of thickness 0.32 mm
Table 1. Fitted Data for Dry Spot profile for the Spreading of SDS on thin liquid film
|
Experiment |
Power law exponent |
Pre-exponential constant |
R – Squared Value |
|
1 |
0.2436 |
29.552 |
0.9956 |
|
2 |
0.2559 |
34.795 |
0.9949 |
|
3 |
0.2441 |
30.597 |
0.9962 |
|
4 |
0.2468 |
28.644 |
0.9931 |
|
5 |
0.2368 |
24.788 |
0.9957 |
The expansion of the dry spot for the case of spreading of trisiloxanes on thin liquid film was irregular i.e. there was jumps making the estimation and the spreading profile with respect with time uncertain. Plots showing the dry spot phenomena for of EO6, EO7, EO8 and EO9 on Petri dish of 15 cm diameter and thickness of the thin liquid of 0.32 mm are shown in Figure 5, Figure 6, Figure 7 and Figure 8 respectively and the point of irregularity were indicated.
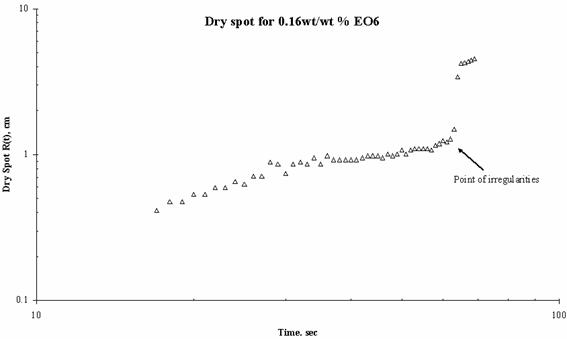
Figure 5. Dry Spot Profile for 3μl drop of EO6 spreading on thin water film of thickness 0.32 mm
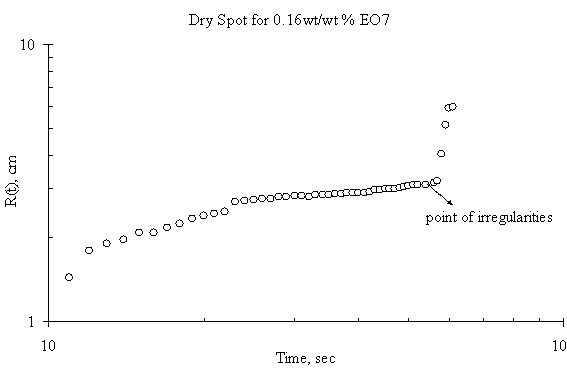
Figure 6. Dry Spot Profile for 3μl drop of EO7 spreading on thin water film of thickness 0.32 mm
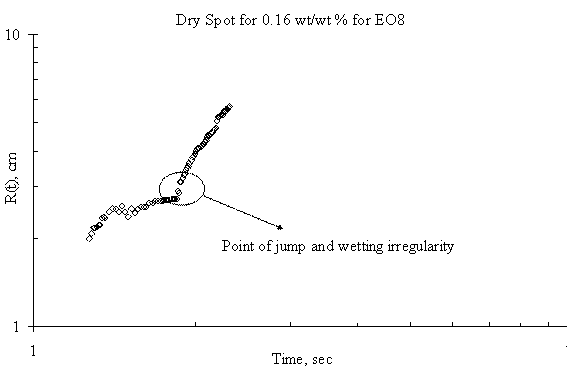
Figure 7. Dry Spot Profile for 3μl drop of EO8 spreading on thin water film of thickness 0.32 mm
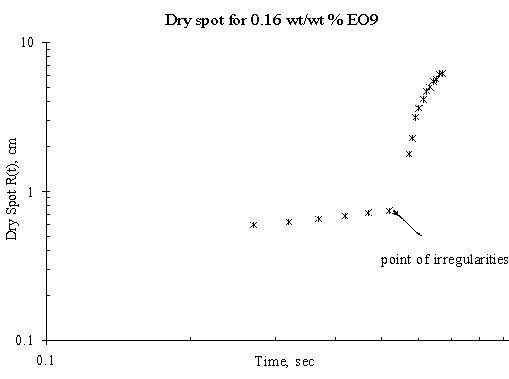
Figure 8. Dry Spot Profile for 3μl drop of EO9 spreading on thin water film of thickness 0.32 mm
The experimental results, however, show mean random behaviour for the dry spot profile for trisiloxanes on thin liquid film, the reason for which remains unclear. It may either be the radius of the Petri dish is large enough to accommodate rupture or the Petri dish is not clean enough. The moving front is so fast that it gets to the edge of the dish and generates a back wave disturbances that tends to alter the progression of the dry spot. A larger Petri dish could be used to verify this, although the research did not go further to investigate it. Another reason could be that the thin film dewets as the superspreading proceeds. The dewetting phenomena may be caused by a strong disjoining pressure generated by the trisiloxanes solution on the thin film or the Petri dish on which the thin film was formed.
Another interesting phenomenon was observed when Petri dish is not properly cleaned before conducting another experiment. The thin film tends to dewet on the surface of the Petri dish, hence increasing the degree of irregularity in the expansion of the dry spot. If the surface of the solid substrate is not clean enough, any little disturbance arising from the Marangoni stress created by the spreading of the surfactant will cause the remaining continuous thin film to dewet. Hence, there will be a change in the spreading profile of the dry spot. This was one of the precautions that were identified during the experiment. Previous works have reported similar phenomena. It has been said that stable films can dewet only through the nucleation of a hole in the film [10]. This may be as a result of heterogeneities on the solid–liquid interface, such as defects [17] or chemical patterning [18] or on the air–liquid interface, such as dust particles or surface active agents [6]. These cause local changes in the chemical potential giving rise to flows that amplify the initial disturbance, thus setting up the conditions that give rise to rupture and the formation of a dry patch or hole.
There was also a time lag between the onset of the fast spreading and the onset of the dry spot. Although the experiment did not model it, however, careful observation revealed that the time lag for SDS was shorter than that of trisiloxanes. Furthermore, different lengths of time lag exist among the various trisiloxanes investigated. The reason could be link to the different disjoining pressure each of the surfactants exhibit at the liquid-liquid interface.
Conclusions
This paper reports the results of an experimental investigation of trisiloxane surfactants and SDS; this is a companion paper to another submitted by the same author to LJS [4]. Both surfactants follow two stages of spreading of the moving front but exhibited different form in the dry spot profile. The results show that the dry spot profile of SDS follow power law of R(t) ~ t0.25 while there were irregularities in the dry spot profile for the trisiloxanes surfactant EO6, EO7, EO8 and EO9. The irregularities were attributed to disjoining pressure of the trisiloxanes on the thin film, partial cleaned solid substrate on which the thin film was formed and back wave disturbances developed from the spreading moving front.
Acknowledgement
The author is grateful to Dr. Randal M. Hill of Dow corning USA for supplying the trisiloxanes and to Professor Victor M. Starov and Ms Polina Prokopovich both of Loughborough University, UK for their fruitful discussion on the study.
References
1. Miksis M. J., Vanden-Broeck J.-M., Motion of a Triple Junction, J. Fluid Mech., 2001, 437, p. 385-394.
2. Kriegsmann J. J., Miksis M. J., Steady Motion of A Drop along a Liquid Interface, SIAM J Appl. Math., 2003, 64(1), p. 18-40.
3. Harkins W. D., The Physical Chemistry of Surfaces Films, Reinhold, New York, 1952.
4. Njobuenwu D. O., Spreading of Trisiloxanes on Thin Water Film: Moving Front Profile, Leonardo J. Sciences, 2007, 6(10), p. 165-178.
5. Warner M. R. E., Craster R. V., Matar O. K., Dewetting of Ultra-thin Surfactant-Covered Films, Phys. Fluids, 2002, 14(11), p. 4040- 4054.
6. Kheshgi H. S., Scriven L., Dewetting: nucleation and growth of dry regions, Chem. Eng. Sci., 1991, 46(2), p. 519-526.
7. Redon C., Brochard-Wyart F., Rondelez F., Dynamics of Dewetting, Phys. Rev. Lett., 1991, 66(6), p. 715-718.
8. Haidara H., Vonna L., Schultz J., Instability and dewetting of confined thin liquid films in nonmiscible external bulk fluids (water and aqueous surfactant solutions): experiments vs. theoretical predictions, Langmuir, 1998, 14(12), p. 3425-3434.
9. Brochard-Wyart F., Martin P., Redon C., Liquid/Liquid Dewetting, Langmuir, 1993, 9(12), p. 3682-3690.
10. Afsar-Siddiqui A. B., Luckham P. F., Matar O. K., The spreading of Surfactant Solutions on Thin Liquid Films, Adv. Colloid and Interface Sci., 2003, 106(1), p. 183-236.
11. Zhu X., Miller W., Scriven L., Davis H., Superspreading of Water-Silicone Surfactant on Hydrophobic Surfaces, Colloids Surf. A, Physicochemical and Eng. Aspects, 1994, 90(1), p. 63-78.
12. Churaev N. V., Esipova N. E., Hill R. M., Sobolev V. D., Starov V. M., Zorin Z. M., The Superspreading Effect of Trisiloxane Surfactant Solutions, Langmuir, 2001, 17(5), p. 1338-1348.
13. Starov V. M., de Ryck A., Velarde M. G., On the Spreading of an Insoluble Surfactant over a Thin Viscous Liquid Layer, J. Colloid & Interface Sci.,1997, 190(1), p. 104-113.
14. Dutschk V., Sabbatovskiy K. G., Stolz M., Grundke K., Rudoy V. M., Unusual Wetting Dynamics of Aqueous Surfactant Solutions on Polymer Surfaces, J. Colloid Interface Sci., 2003, 267(2), p. 456-462.
15. Fraaije J. G. E. M., Cazabat A. M., Dynamic of Spreading on a Liquid Substrate, J. Colloid Interface, 1989, 133(2), p. 452-460.
16. Jensen O. E., Grotberg J. B., Insoluble Surfactant Spreading on a Thin Viscous Film: Shock Evolution and Film Rupture, J. Fluid Mech., 1992, 240, p. 259-288.
17. Jacobs K., Herminghaus S., Mecke K. R., Thin Liquid Polymer Films Rupture via Defects, Langmuir, 1998, 14(4), p. 965-969.
18. Kargupta K., Konnur R., Sharma A., Spontaneous Dewetting and Ordered Patterns in Evaporating Thin Liquid Films on Homogeneous and Heterogeneous Substrates, Langmuir, 2001, 17(4), p. 1294-1305.
Nomenclature
|
Symbols |
Subscripts |
|
n = exponents |
L = liquid |
|
R(t) = radius of the drop base |
V = vapour |
|
SLS = spreading coefficient |
S = substrate |
|
t = time |
Acronyms |
|
Greek |
CMC = Critical Micelle Concentration |
|
μ = dynamic viscosity of the liquid |
EO = Polyethylene Oxide |
|
ρ = liquid density |
EO6 = Trisiloxane with Six Polyethylene Oxide chain length |
|
γLS = liquid-substrate interfacial tension |
EO7 = Trisiloxane with Seven Polyethylene Oxide chain length |
|
γLV = liquid-vapour interfacial tension |
EO8 = Trisiloxane with eight Polyethylene Oxide chain length |
|
γSV = substrate-vapour interfacial tension |
EO9 = Trisiloxane with nine Polyethylene Oxide chain length |