On an Inverse Semi-Group which is Simple but Not Completely Simple
Lawrence N. EZEAKO
Department of Mathematics and Computer Science, Federal University of Technology, Minna, Nigeria
Abstract
W. D. Munn, (1966) has shown that if E is a semilattice, then the Munn semigroup TE of E is an inverse semigroup whose semilattice of idempotents is isomorphic to E. If E is a uniform semillatice, then TE is a bisimple inverse semigroup. J. M. Howie, (1976) proved that up to isomorphism, the only fundamental bisimple semigroup S, having
E = CW = { e0, e1, e2,………………} with e0> e1> e2
Is the Bisyclic semigroup. In this paper is highlighted the structure of the Bicyclic semigroup and prove that every simple semigroup which has idempotent, none of which is primitive, must necessarily be a web of bicyclic semigroups.
Keywords
Bicycle Semi-Group Structure; Inverse Semi-Group; Simple Semi-group; Bisimple Semi-Group, Completely Simple Semi-group
Preliminaries
Construction
Let X be a 2- element set, i.e. X = { p,q}. We construct a semigroup B, from X by letting all elements in B, be of the form qm pn, m and n are nonnegative integers. We also let pq = p0 = q0 = 1. Then each element qm pm Î B is unique. It is trivial to show that B is indeed a semigroup under the composition, multiplication.
Definitions
1 Let a, b Î S, where S is a semigroup. Then a and b are (generalized) inverse of each other if aba = a and bab = b. S is called an inverse semigroup if every element of S has a unique inverse in S.
2 A semigroup S, is simple if S has no proper ideals
3 For every element a, b is a semi group S,
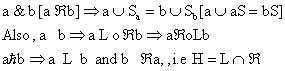
4 A semigroup S, is bisimple (i.e. D – simple) if S consist of a simple D-class.
5 A completely simple semigroup is a semigroup which contains a primitive idempotent.
Propositions
1. The semigroup B, constructed in section 1.1 above is the Bicyclic Semigroup. It is an inverse semigroup which is bisimple (hence simple), with an identity element. The idempotent of B are of the form.
![]()
And so B has no primitive idempotent i.e B is not completely simple (Prop. 1)
2. Every simple semigroup which has idempotents, none of which is primitive, must contain B. Such a seigroup has not be a “web of B’ s” (Prop. 2)
Proof of Propositions
Proof of Prop 1
1. B is an inverse Semigroup
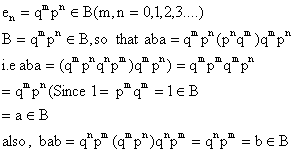
Hence B is an inverse semigroup.
2. B is a Bisimle Semigroup
Let
a ![]()
We now show that a  b [a L b]
i.e. aB = bB = B [Ba = Bb = B]

We cannot compare aB and bB under these conditions. So we let ![]() and let min
[m,n] = (m,n) and define
and let min
[m,n] = (m,n) and define
![]()
Then let ![]() which is possible
which is possible
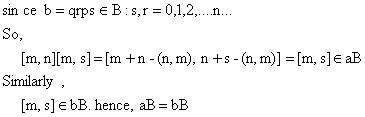
i.e. a  b
Conversely; suppose that [m,n] Â [r,s], then there exist
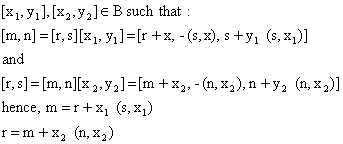

Existence and Nature of Idempotents in B
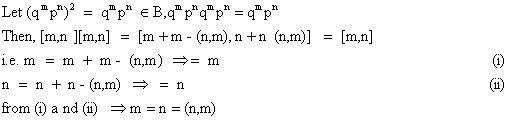
Thus the idempotents of B are of the form en = qnpn (n = 0,1,2,3,……….)
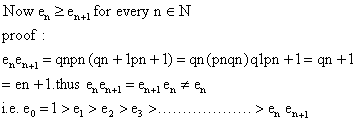
Thus B has no primitive idempotent
Þ B is a Bisimple semigroup Þ B is a simple semigroup
Þ B is not completely simple.
The H – classes of B and the Left [Right] ideals of B

Hence the H-class of B are the singletons ![]()
Left Ideals: Let L be a left ideal of B. Then L = ÈB b, b ÈÎL

Proof of Prop. 2
Theorem 1
Let e be a non – primitive idempotent of a simple semigroup S, which is not completely simple. Then S contains a bicyclic subsemigroup which has e as their identity element.
Lemma 1
Let e, Ia, Ib, be elements of a semigroup S, such that; ea = ae = a; eb = be = b, ab =e
But ba ¹ e. Then every element of the subsemigroup generated by a and b is uniquely expressible as bman where m,n are nonnegative integers.
And a0 = b0 = e0. Hence the subsemigroup of S generated by a and b is isomorphic to the bicyclic semigroup B
Proof of Lemma I
S is infinite: We prove that an ¹ ar for 1 £r<n
For all nonnegative integer n.
![]()
(which is a contradiction). So, a2 ¹ a.
Suppose that a, is such the an ≠ ak, for 1 ≤ k < n.
Let r be such that 1 ≤ r ≤ n + 1 and an+1 = ar
Then an(ab) = ar-1(ab) Þ ane = ar-1e Þ an = ar – 1, but 1 ≤ r ≤ n-1 Þ 1 ≤ r -1 < n, hence an+1 ≠ ar for 1 ≤ r ≤ n+1.
We conclude that {an; n = 0, 1,2,3,………..} is infinite.
So, S is infinite.
Also, anbmÞaman = ambm Þ am+n = e = a0 by the above reasoning. i.e. m + n = 0. But both m and n are nonnegative integer so we must have m = n = 0.
Thus an ¹ bm unless m = n = 0.
Now, suppose that; bnam = bras, we may assume that n £ r, without loss of generality.
Thus we have;
![]()
Hence the expression bnam is unique.
Therefore the subsemigroup generated by {a,b} is isomorphic to the bicyclic semigroup B.
Proof of Theorem I
Let e Î S be a non–primitive idempotent. Then there exits an idempotent e1 Î S, say, such that
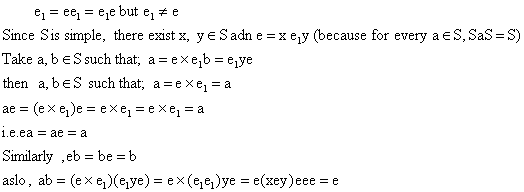
![]()
Þ e = e1 (which is a contradiction!!) since e ¹ e.
So ba ¹ e. Hence the conditions in Lemma I are satisfied. So the bisyclic subsemigroup generated by {a,b} is a subsemigroup of S containing e as an identity element.
Conclusion
From theorem I and the structure of the bicyclic semigroup B, thus discussed, it is evident that any semigroup S, which is simple, and which contains a non-primitive idempotent which acts as an identity element, must comprise a “web of B’s.”
Acknowledgements
I sincerely wish to thank Professor K. R. Adeboye, (former Dean, School of Science Education, Federal University of Technology, Minna) for his very useful comments on an earlier draft of this paper.
References
1. Howie J. M., An Introduction To Semigroup Theory, Academic Press, London, 1976.
2. Munn W. D., Uniform Semilattices and Bisimple. Inverse Semigroup, Quart .J. Math, Oxford, 1966, 17, p. 151-159.
3. Reilly N. R., Bisimple w-semigroups, Proc. Glasgow Math. Assoc., 1966, 7, p. 160-167.
4. Warne R. J., I-bisimple Semigroups, Traner. Amer. Math. Soc., 1968, 130, p. 367-386.