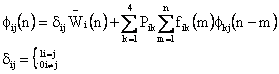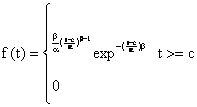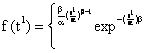A Stochastic Model in Discrete States and Discrete Time for the Control of Leprosy Disease
Usman Yusuf ABUBAKAR
Department of Mathematics and Computer Science, Federal University of Technology, Minna, Nigeria
Abstract
This paper presents the use of Semi-Markov model in discrete state and discrete time to study the condition of leprosy patients. Leprosy is considered to be controlled if is possible to maximize recovery and consequently minimize relapse and death. The model takes into account the concept of effectiveness of the treatment. The result shows that it is possible to attain a zero probabilities for a relapse and death from leprosy when the treatment is very effective. The model could be used to predict the cases of leprosy disease. The predictions could be used for planning resources for the control of leprosy.
Keywords
Stochastic; Semi-Markov; Interval; Transition; Probability; Leprosy, Control
Introduction
Policy makers and administrators in the health industry take into account quantitative predictions from stochastic models on decision-making policies. Leprosy is an infectious disease of the skin and nerves. It is caused by a mycobacterium leprae, often resulting into the deformity of the body peripherals like the fingers and toes. It can be treated and cured.
Several mathematical studies of leprosy have been reported including [1] that have studied the prevalence rate and the incidence of new cases. A study on the Leprosy rates in villages of different distance apart has been presented in [2]. Semi-Markov models have been used to study relapses from leprosy after treatment with Dapsone and MDT regimen respectively, [3]. In this paper, we apply the principles of semi-markov process in discrete states and time to study cases of recovery and death in addition to relapses from leprosy.
The model
Consider stochastic process íXn, n = 0, 1, 2, …ý that takes on a finite or countable number of possible values such that:
|
|
(1) |
for all states i0, i1,…,in-1,i,j and all n≥0. Such a stochastic process is known as a Markov chain [4]. Since probabilities are nonnegative and since the process must make a transition into some state, we have that.
|
|
|
Let us consider a process whose successive state occupancies are governed by the transition probabilities of a Markov chains in (1), but whose stay in any state is described by a random variable that depends on the state to which the next transition is made such a process is referred to as a semi-Markov process [5].
Whenever the patient enters state ‘i’ he remains there for a time Tij in state i before making a transition to state ‘j’. Tij is called the ‘holding time’ in state i. The holding times are positive integer valued random variables each governed by a probability distribution function fij ( ) called the holding time distribution function for a transition from state i to state j.. Thus P(Tij = m) = fij (m). m = 1, 2, 3, . . . i, j =1, 2, 3, 4.
The states transition probabilities and the holding time in the states before the transition is made describes a semi-Markov process. Thus, we have to specify holding time distribution functions in addition to the transition probabilities. For a fixed value of i, Tij is the same for each value of j, (i, j = 1, 2, 3, 4) [5].
Let Fij ( ) be the probability distribution of Tij.
|
Fij (n)
= P(Tij £ n) = |
|
and ![]() ( ) be the complementary probability
distribution of Tij.
( ) be the complementary probability
distribution of Tij.
|
|
|
Suppose the patient enters state i. Let Yi be the time he spent in state i before moving out of the state i. Then Yi is called the waiting time in state i.
We let ![]() (n) be the probability
distribution function of Yi. Then
(n) be the probability
distribution function of Yi. Then
|
wi (m) = P(Yi
= m) = |
|
The probability distribution Wi ( ) and the complementary cumulative probability distribution Wi ( ) for the waiting times are given as follows
|
Wi (m) = P(Yi
£ n) = |
|
and
|
= |
(2) |
Interval Transition Probabilities
We define ![]() (n) to be the probability that
the leprosy patient will be in state j in time n given that he
entered state i in time zero. This is called the interval transition
probability from state i to state j in the interval (0, n]. Then
(n) to be the probability that
the leprosy patient will be in state j in time n given that he
entered state i in time zero. This is called the interval transition
probability from state i to state j in the interval (0, n]. Then
|
i, j = 1, 2, 3, 4, n = 1, , 3, . . . . |
(3) |
![]() (n)
is as defined in (2) [6].
(n)
is as defined in (2) [6].
The Weibull Distribution
The holding time in the states is described by the Weibull probability distribution function. The probability mass function of a discrete random variable T having the three parameter Weibull distribution is given by
|
t < 0, a, b, c > 0 |
|
The scale parameter is α, the parameter β determines the shape and it is therefore called the shape parameter, the location parameter is c.
We can reduce the distribution to a two parameter Weibull by putting t1 = t - c, thus
|
a, b > 0 |
|
The parameters of the distribution have been estimated using percentile points presented in [7].
Model Assumptions
It is assumed that the transition from one state to a different state should not occur at time t = 0 (year 0) and that the basic unit of time is one year. A leprosy patient that dies during treatment or during the period of a follow-up is assumed to have died of leprosy. Natural death is not considered. A patient that fails to recover from leprosy after completing a dose of the treatment is considered to have developed a resistance to the drug and is consequently considered to have relapsed.
We consider a leprosy patient. Let us assume that each year the leprosy patient is under treatment or has recovered from the disease or has relapsed or has died from the disease. We therefore have a four state process State 1- Under treatment, State 2- Recovery, State 3- Relapse and State 4- Death due to leprosy. The transition from one state to another is indicated in the transition diagram below.
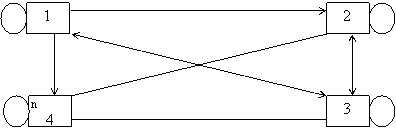
Figure 1. Transition diagram for Leprosy Process
We observe that states 1, 2 and 3 are transient states and state 4 is an absorbing state. In other words, all possible transitions of the process are made between states 1, 2 and 3 but once a transition is made to state 4 the process terminates. We would like a transition to occur at a time the duration of stay in a state is completed, even if the new state is the same as the old. Such a transition is called a virtual transition, and is represented by loops in the transition diagram.
From the above transition diagram we can record the transition probability matrix ‘P’ for the process as shown below.
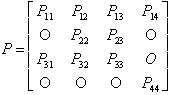
Figure 2 shows a realization of the process.
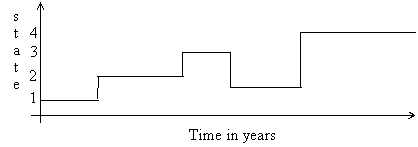
Figure 2. A possible realization of the process
The Effect of Treatment
The effect is measured by the increase in probability of recovery, a decrease in the probabilities of death and having a relapse. This is obtained from the following expressions.
|
E12 = (1 + k)P12 E1j = (1 - k)P1j, j = 3, |
(4) |
where k is a positive real number in the interval [0, 1). Then
|
|
|
and the transition matrix is P with the first row replaced by E1j. i = 1, 2, 3, 4.
Application
A 10- year follow-up of a 6-week quadruple drug regimen for 136 multibacillary leprosy patients showed 13% relapses, seven late and the remaining (111) were considered to have recovered from leprosy [8].
Result
Using equations (3) and (4), we obtain the results
presented in Tables 2-4 and illustrated in figures 3-5 respectively. ![]() (n) is
the probability that a leprosy patient will recover at time n given that the
patient started treatment at time zero, and that the treatment is k effective
at zero percent, fifty percent and ninety-nine percent on the sensitivity
analysis.
(n) is
the probability that a leprosy patient will recover at time n given that the
patient started treatment at time zero, and that the treatment is k effective
at zero percent, fifty percent and ninety-nine percent on the sensitivity
analysis.
Table 2. The probabilities of recovery from leprosy
- ![]() (n)
(n)
|
n |
K = 0 |
K = 0.50 |
K = 0.99 |
|
1 |
0.0095754713 |
0.0143632062 |
0.0190551877 |
|
2 |
0.0220378209 |
0.0330567323 |
0.0438552648 |
|
3 |
0.0356860533 |
0.0535290837 |
0.0710152462 |
|
4 |
0.0496131815 |
0.0744197667 |
0.0987302288 |
|
5 |
0.0632850900 |
0.0949276388 |
0.1259373277 |
|
6 |
0.0763817355 |
0.1145725995 |
0.1519996524 |
|
7 |
0.0887717359 |
0.1330755502 |
0.1765469015 |
|
8 |
0.1001924053 |
0.1502885967 |
0.1993828863 |
|
9 |
0.1107673943 |
0.1661510915 |
0.2204271257 |
|
10 |
0.1204402894 |
0.1806604415 |
0.2396761775 |
|
11 |
0.1292348504 |
0.1938522607 |
0.2571773529 |
|
12 |
0.1371911019 |
0.2057866454 |
0.2730102837 |
Table 3. The probabilities of a relapse from lepros
- 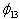 (n)
(n)
|
n |
K = 0 |
K = 0.50 |
K = 0.99 |
|
1 |
0.0063836472 |
0.0031918236 |
0.0000638364 |
|
2 |
0.0146918809 |
0.0073459405 |
0.0001469187 |
|
3 |
0.0237907022 |
0.0118953511 |
0.0002379068 |
|
4 |
0.0330554519 |
0.0165377259 |
0.0003307542 |
|
5 |
0.0421900600 |
0.0210950300 |
0.0004219002 |
|
6 |
0.0509211533 |
0.0254605766 |
0.0005092110 |
|
7 |
0.0591446869 |
0.0295723435 |
0.0005914463 |
|
8 |
0.0667949319 |
0.0333974659 |
0.0006679487 |
|
9 |
0.0738449320 |
0.0369224660 |
0.0007384486 |
|
10 |
0.0802935287 |
0.0401467644 |
0.0008029345 |
|
11 |
0.0861565620 |
0.0430782810 |
0.0008615648 |
|
12 |
0.0914607272 |
0.0457303636 |
0.0009146064 |
Table 4. The probabilities of death from lepros - 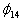 (n)
(n)
|
n |
K = 0 |
K = 0.50 |
K = 0.99 |
|
1 |
0.0031918236 |
0.0015959118 |
0.0000319182 |
|
2 |
0.0073459405 |
0.0036729702 |
0.0000734593 |
|
3 |
0.0118953511 |
0.0059476756 |
0.0001189534 |
|
4 |
0.0165377259 |
0.0082688630 |
0.0001653771 |
|
5 |
0.0213950300 |
0.0105475150 |
0.0002109501 |
|
6 |
0.0254605766 |
0.0127302883 |
0.0002546055 |
|
7 |
0.0295723435 |
0.0147861717 |
0.0002957231 |
|
8 |
0.0333974659 |
0.0166987330 |
0.0003339743 |
|
9 |
0.0369224660 |
0.0184612330 |
0.0003692243 |
|
10 |
0.0401467644 |
0.0200733822 |
0.0004014672 |
|
11 |
0.0430782810 |
0.0215391405 |
0.0004307824 |
|
12 |
0.0457303636 |
0.0228651818 |
0.0004573032 |
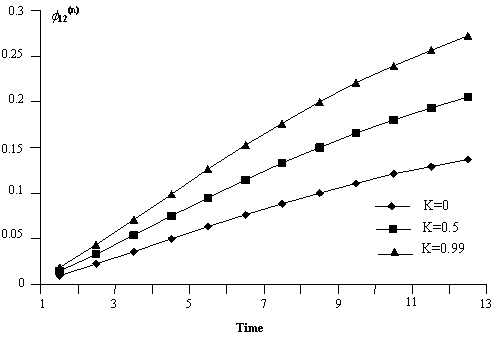
Figure 3. The graph of the probabilities of recovery from leprosy
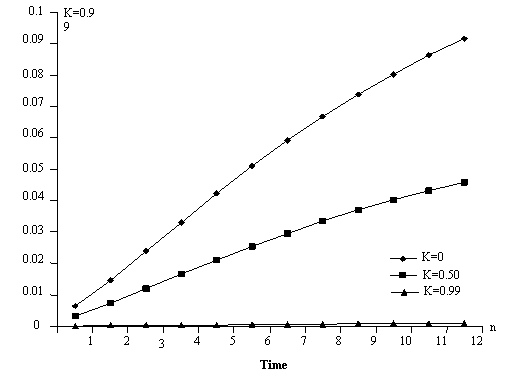
Figure 4. The graph of the probabilities of a relapse from leprosy
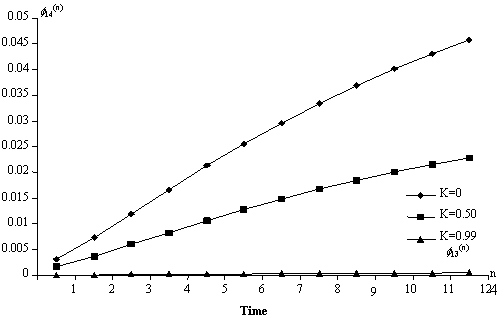
Figure 5. The graph of the probabilities of death from leprosy
Discussion
The result presents the concept of control of leprosy such that cases of recovery are maximized and consequently minimizing the incidence of relapse and death due to leprosy. We observed from the tables and the graphs that when the treatment is 99% effective (k = 0.99), the probabilities of relapse and death from leprosy has been reduced to zero and consequently increased the probability of recovery to unity.
Semi -Markov model could be used as a predictive device to study leprosy conditions. Such predictions could be useful to the government and non-governmental organizations for the management of resources for the control of leprosy disease.
References