On Primitive Abundant Semigroups and PA-Blocked Rees Matrix Semigroups

 

Lawrence N. EZEAKO

 

Department of Mathematics and Computer Science, Federal Univesity of Technoly, Minna, Nigeria

abochoche@gmail.com

 

 

Abstract

In this paper we utilize Warne’s homomorphism theorem for bisimple inverse semigroups with an identity element [13, Theorem 1.1] to prove the theorem: Every primitive abundant semigroup with a zero element is isormorphic to a PA-blocked Ree’s matrix semigroup.

Our approach obviates the tedium of the proof of the existence of a homomorphic mapping (see Markie, 1975) in order to prove the same theorem.

Keywords

Bisimple; Inverse; Semigroups; Primitive Abundant Semigroups; Ree’s Matrix Semigroups; Homomorphism

 

 

Preliminaries

 

Ree’s matrix Semigroup (A completely O-Simple Semigroup)

Let G º a simple group with identity e

P º matrix (pm with entries from the zero group G0, where

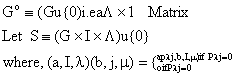
G0 º (GỤ{0} i.e. a L × I matrix

Let S = (GxIxL)u {0}

where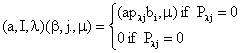

 

Then S thus constructed is completely O - simple, and S º Mo [G,I,L,P] is the I × L, Ree’s matrix semigroup over the O-group Go, with the regular sandwich matrix P.

 

 

The PA - blocked Ree’s Matrix Semigroup

D. Rees [9] has shown that we can construct a semigroup from a set of monoids and bisystems over these monoids. Such a construction generalizes Rees matrix semigroup. Under certain conditions (see [9]) such as semi group becomes abundant, with all its non-zero idempotents primitive. It is called a PA-blocked Rees matrix semmigroup.

 

Important remarks: Since S is O-Simple

·        {0} and S are the only ideals of S

·        S x S ¹ 0

·        "aÎ s/ {0}; aS = Sa = S

Also, since S is completely 0 - simple, S satisfies the MinL, MinR conditions i.e every non-empty set of the l - classes or the R-classes possesses a minimal member

 

Right [Left] S- Systems

If M is a set and S is a monoid then M is a right S-system if there exists a mapping (x,s) ® xs from M x S into M, with the properties that

i.         

ii.         

a left S - system is dually defined. If S and T are monoids, then M is an (St) - Bisystem, where M is a left S - system as well as a right T - system and for each

we have

 

If M is a right S - system and N is a left S - system and  is an equivalence relation on M N generated by the subset  of , then the set , simple, is called the tensor Product over S, of the two S-systems

* using these definition we make the following propositions

 

 

Propositions

Let e, f be idempotent of a primitive abundant semigroup S, with zero, if e, f are not D-related and if ef, fe are both non-zero, the;

1.      H* ef and H* fe are cancellative subsemigroups of S without identities

2.      /H*e/ = /H * ef/ = /H* fe/ = /H* f/

3.      H* ef is isomorphic as a semigroup and as a right H* f - system to a left idea of H*f, and isomorphic as a semigroup and as a left H*e - system to a left ideal of H*e

 

Proof of Proposition 1

 

Proof of Proposition 2

Since

                                                                                              (a)

Also, if x Î H* f, then Fx Î H* f and ex = x

Thus

If x1, x2 Î H* f and fx1 = fs2, then

                                                                                     (b)

From (a) and (b) Þ /H*f/ = /H* ef/

Similarly, /H* ef/ = H*el

and 2 is proved.

 

Proof of Proposition 3

Let

Also,

For each

Furthermore, for any

So, F is a semi group isomorphism

Similarly, we can show that H* ef is isomorphic as

a left H* e - system to a left ideal H*e

i.e. 3 is proved.

 

 

                        Construction of a Primitive Abundant Semigroup S, with Zero

 

 

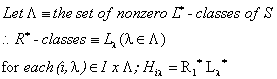
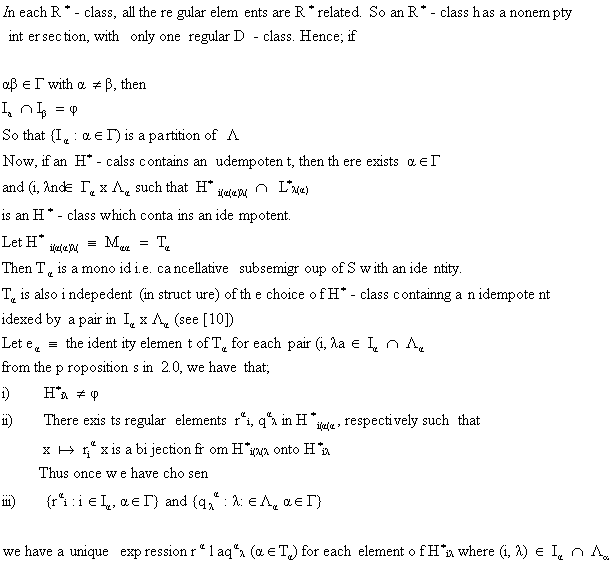
                        Main Theorem

 

            Every primitive Abundant Semigroup as constructed in (3.0) above is Isomorphic to A PA-Block Rrees Matrix Semigroup

 

                        Proof of Main Theorem

 

 

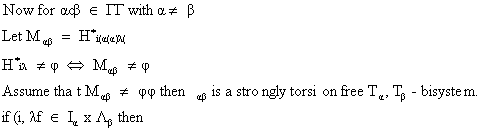
Conclusion

 

We have thus proved in  a very simple manner i.e. without recourse to the necessity for the existence of a homomorphic mapping,-that every primitive abundant semigroup with a zero, is isomorphic to a PA - blocked Rees Matrix semigroup

Acknowledgements

 

            I sincerely wish to thank Professor K. R. Adeboye, former Dean School of Science and Science Education, Federal University of Technology, Minna, for his useful comments on an earlier draft of this paper.

 

 

References

 

1.      Armstrong S., The Structure of Type A Semigroups, Semigroup Forum 1984, 29, 319-336, Springer Verlag, New York, Inc.

2.      Clifford H., Preston G. B., The Algebraic Theory of Semigroups, Math. Surveys, 1961, 7(1) & 1967, II Amer. Math. Soc. Providence, R.I.

3.      Fountain J. B., Adequate Semigroups, Proc. Edin. Math. Soc., 1979, 22, p. 113-125

4.      Fountain J. B., Adequate Semigroups, Proc. London Math. Soc., 1982, 44(3), p. 103-129

5.      Howie J. M., An Introduction To Semigroup Theory, Academic Press, 1976.

6.      Markie L., On Locally Regular Rees Matrix Semigroups, Acta. Sci. Math (Szeged), 1975, 37, p. 95-102.

7.      Munn W. D., A Class of Irreducible Matrix Representation of an Arbitrary Inverse Semigroup, Proc. Glasgow Math. Assoc., 1961, 5, p. 41-48.

8.      Pastigin F., A Representation of a Semigroup of Matrices Over a Group with Zero, Semigroup Forum, 1975, 10, p. 238-249.

9.      Rees D., On Semigroups, Proc. Cambridge Philos. Soc., 1940, 36, p. 387-400.

10.  Rees D., On The Ideal Structure of a Semigroup Satisfying a Cancellation Law, Quant. J. Math. Oxford Ser., 1948, 19(2), p. 101-108.

11.  Reilly M. R., Clifford A. H., Bisimple Inverse Semigroup as Semigroups of Ordered Triples, C and .J. Math., 1968, 20, p. 25-39.

12.  Steinfeld O., On a Generalization of Completely O-Simple Semigroups, Acta. Sci. Math. (Szeged), 1967, 28, p. 35-46.

13.  Warne R. J., Homomorphisms of a - Simple Inverse Semigroups with Identity Pacific, J. Math., 1964, 14, p. 1111-1122.