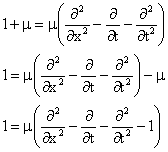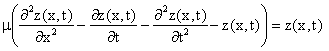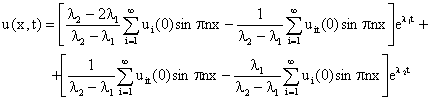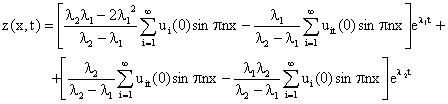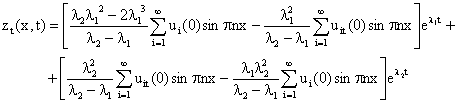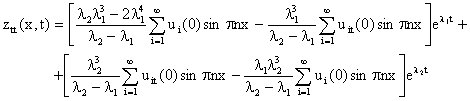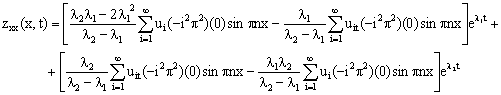Penalty Cost for One-Dimensional Energized Wave Equatio from Leonardo Journal of Sciences

Penalty Cost for One-Dimensional Energized Wave Equation

Victor O. WAZIRI^1* and Sunday A. REJU²

¹Federal University of Technology, Mathematics & Statistics & Computer Science Department, Minna. Nigeria

²National Open University of Nigeria, Victoria Island, Lagos, Nigeria

^*dronomzawaziri@yahoo.com, sreju@nou.edu.ng

Abstract

This paper constructs the penalty cost functional for optimizing the one-dimensional energized wave control operator. In some multiplier methods such as the Lagrange multipliers and Conjugate Gradient Method (CGM), the cost of augmenting the dynamical constraint equation into an unconstraint formulation involving an integral objective functional is guessed. The Extended Conjugate Gradient Method (ECGM) demands that the penalty cost functional be determined by computational procedure. The functional is completely given in terms space x and time dependent variable t.

Keywords

Penalty Cost; Hilbert Space; Extended Conjugate Gradient Method (ECGM).

Introduction

We intend obtaining the numerical values for the penalized penalty function μ(x,t) ≥ 0, from which the numerical values for the penalized cost functional shall be determined iteratively using program codes. The computational derivation of the penalty cost is be retrospection to the previous derived equations of the control operator in [1].

The analysis of the problem

Recall the control operator B in [1]. We assume that the control operator is bounded in a Hilbert Space. As a Hilbert space, it is a linear, self-adjoint and bounded control operator. Being self-adjoint means that the elements of the control operator B21 and B12 are symmetric positive definite. Hence akin to [2] and [3], it would not be difficult to present the following results:

	(1)
	(2)

Equations 1 and 2 become:

	(3)
	(4)

By definition, equations 3 and 4 are symmetrical and hence are equivalence. Thus:

(5)

Therefore,

(6)

implying logically that:

(7)

The action of the state on equation 7 is:

(8)

But therefore the penalty must be absolutely defined such that:

(9)

where zero is not defined on the denominator since μ ≥ 0.

The analytical control solution is:

(10)

The analytical state solution is:

(11)

From equation 11, the following differential equations are in order:

	(12)
	(13)
	(14)

Substituting the derived equations 11 through to 14 into equation 8 would yield the desired penalty cost functional. The program codes for the penalty functional from [3] yields the following numerical outputs in the table 1 below:

Table 1: The output for the penalty cost constant

s/n	Dimensional space n	Penalty Cost
1	2	14330.9164901865
2	10	917492.21798227
3	20	146929949.200521
4	30	743956452.263497
5	40	2351406642.63868
6	50	5740893606.37407
7	60	119044913112.581

Conclusion

As in [4] were rightly observed, the penalty cost constant that augments a quadratic integral objective functional 1 with the dynamical energized wave equation to adjoin the unconstrained equation 3 must be sufficiently large on one hand; on the other hand, this parameter must not approach infinity. If it does, the convergence rate will deteriorate sharply. This would cause numerical instability because the derivatives of the penalty functional would increase without bounds near the minimum. Therefore, there would be a paradox.

A clear observation of the penalty cost numerical values in table 1 maintains a stable numeric values. Since the penalty numerical values maintain stability, they could be useful tools in the implementation of the ECGM computational algorithm, as they shall be applied in the final paper of this series such as to obtain the optimal control and state numerical solutions.

References