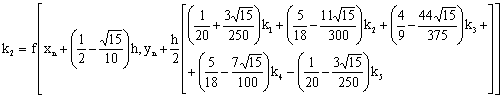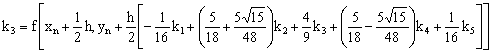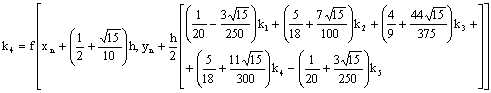Symmetric Uniformly Accurate Gauss-Runge-Kutta Method
Dauda Gulibur YAKUBU*1, Samaila MARKUS2, Amina HAMZA2 and Abubakar Muhammad KWAMI1
1Mathematical Sciences Program, Abubakar Tafawa Balewa University,Bauchi, Nigeria 2Department of Mathematics and Statistics, University of Maiduguri, Maiduguri, Nigeria
Abstract
Symmetric methods are particularly attractive for solving stiff ordinary differential equations. In this paper by the selection of Gauss-points for both interpolation and collocation, we derive high order symmetric single-step Gauss-Runge-Kutta collocation method for accurate solution of ordinary differential equations. The resulting symmetric method with continuous coefficients is evaluated for the proposed block method for accurate solution of ordinary differential equations. More interestingly, the block method is self-starting with adequate absolute stability interval that is capable of producing simultaneously dense approximation to the solution of ordinary differential equations at a block of points. The use of this method leads to a maximal gain in efficiency as well as in minimal function evaluation per step.
Keywords
Block Method; Collocation Polynomial; Continuous Scheme; Gauss-Runge-Kutta Method; Multistep Collocation; Symmetric Scheme;
Subject Classification
AMS 65L05
Introduction
There are many
collocation schemes and more generally Runge-Kutta schemes which are symmetric
and A-stable, for the resolution of the Cauchy problem associated with y ![]() (I) where I
is an interval of R containing the point x0 such that:
(I) where I
is an interval of R containing the point x0 such that:
|
|
(1.1) |
where f(x, y) is a given real valued function in the strip s = I × (-∞, +∞) which is continuous with respect to both variables. Collocation at Gauss-points is well known to be equivalent to a family of Runge-Kutta schemes with highest order of accuracy for a given number of stages, [1]. However, these schemes also have the well known disadvantages of being fully implicit and usually extra stages are introduced to enhance stage–order in the Gauss-Runge-Kutta method [8]. In this work, an attempt is made to eliminate the drawback of being fully implicit by providing sufficiently accurate simultaneous difference equations from a single symmetric continuous hybrid formula. Hence by the evaluation of the single symmetric continuous hybrid formula the discrete schemes obtained are not fully implicit and are strongly stable at infinity [4], suitable for both non-stiff and stiff initial value problem in ordinary differential equations. This is achieved by involving the Gauss-points for both interpolation and collocation, because the Gaussian points are naturally continuous along with their first derivatives. Further, to avoid the introduction of extra stage order [8] in the Gauss-Runge-Kutta method, this paper suggests linearly partitioning of the step [xn, xn+1] into segments that are separated by the Gauss points, that is
|
|
(1.2) |
Construction of Symmetric Gauss-Runge-Kutta Method
Consider a collocation polynomial [7] of the form
|
|
(2.1) |
where t denotes the number of
interpolation points xn+j, j = 0,1,…,t-1; and m denotes the distinct
collocation points ![]() Î[xn, xn+k], j = 0, 1,…, m-1 belonging
to the given step. The step size h can be variable it is assumed in this paper
as a constant, for simplicity, with the given mesh xn: xn
= x0 + nh, n = 0, 1, … N where h = xn+1 – xn,
N = (b-a)/h. Also we assume that (1.1) above for the first order system of
ordinary differential equation, has exactly one solution and Φj(x)
and Ψj(x) in (2.1) to be represented by polynomials of
the form
Î[xn, xn+k], j = 0, 1,…, m-1 belonging
to the given step. The step size h can be variable it is assumed in this paper
as a constant, for simplicity, with the given mesh xn: xn
= x0 + nh, n = 0, 1, … N where h = xn+1 – xn,
N = (b-a)/h. Also we assume that (1.1) above for the first order system of
ordinary differential equation, has exactly one solution and Φj(x)
and Ψj(x) in (2.1) to be represented by polynomials of
the form
|
|
(2.2a) |
|
|
(2.2b) |
with constant coefficients Φj,i+1(x) and hΨj,i+1(x) to be determined. Putting (2.2) into (2.1) we have
|
|
(2.3) |
Writing
|
|
|
such that (2.3) reduces to
|
|
(2.4) |
which can now be express in the form
|
|
|
Thus we can express equation (2.4) explicitly as follows
|
|
(2.5) |
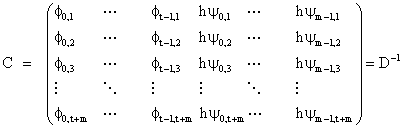
where
|
|
(2.6) |
of dimension (t + m) × (t + m) and
|
|
(2.7) |
We call D the multistep collocation matrix which has a very simple structure and of dimension (t + m) × (t + m). As can be seen the entries of C are the constant coefficients of the polynomials given in (2.2) and (2.3) which are to be determined.
Symmetric Gauss-Runge-Kutta Method from Uniformly Accurate Order Five-Block Scheme
Here we derive the continuous single hybrid scheme and evaluate the continuous scheme to obtain the uniformly discrete formula. The Gaussian points are obtained from the roots of Lm(x) of degree m Legendre polynomial valid in the interval [xn, xn+1]. For the upgrading [6] of the Gauss Runge-Kutta method, that is to have uniform order 5 (superconvergence) through out the interval of integration, we set s =3, t = 3, and the matrix D of equation (2.7) takes the form:
|
|
(3.1) |
Inverting the matrix D in equation (3.1) once and using some algebraic simplifications we obtained the continuous scheme as
|
|
(3.2) |
where
|
|
Evaluating equation (3.2) at the point xn and xn+1 and its first derivative at xn and xn+1 we obtained the following 4-block finite difference scheme with uniformly accurate order five.
|
order p = 5, C6 = 6.25 × 10-5 |
(3.3a) |
|
order, p = 5, C6 = 6.25 × 10-5 |
(3.3b) |
|
order, p = 5, C6 = 7.5 × 10-4 |
(3.3c) |
|
order, p = 5, C6 = 7.5 × 10-4 |
(3.3d) |
Solving the block finite difference scheme ((3.3)a-d) simultaneously we obtained the following symmetric accurate discrete schemes:-
|
|
(3.4a) |
|
order p = 5, C6 = 6.94 × 10-7 |
(3.4b) |
|
order p = 5, C6 = -8.68 × 10-6 |
(3.4c) |
|
|
(3.4d) |
We converted the block discrete scheme (3.4a)-(3.4d) to symmetric Gauss Runge-Kutta method
|
|
(3.5) |
|
|
|
Remark
It is important to note that xn and xn+1 are not used as collocation points in contrast to Lobatto method [3] page 229. In the resulting formulae (3.3a)-(3.3d), y'(xn) = fn and y'(xn+1) = fn+1 which are just additional function evaluations introduced not by collocation. Equation (3.1) above shows that only the s-Gaussian points are involved as collocation points in obtaining the continuous scheme (3.2). The nonlinear equations (3.3a)-(3.3d) can be solved directly to determine the unknowns by the Newton’s method without predictors.
Numerical Applications
Here we present some numerical results to show the performances of the upgraded method. However, it is found that the approximate solutions are very close to the corresponding exact values obtained at the expense of very low computational cost. The maximum errors arising from the computed and exact values at some selected mesh points are presented side by side with results from a known conventional method of the same order for comparison purposes, see [3] page 220.
Application 1
y' = -20y + 20sinx+cosx, y(0) = 1
Exact solution of application 1: y(x) = e-20x + sinx (see Table 1)
Application 2
y' = x + y, y(0) = 1
Exact solution of application 2: y(x) = 2ex – x – 1
Application 3
y' = - y, y(0) = 1
Exact solution of application 3: y(x) = e-x (see Table 3)
Table 1. Absolute errors of numerical solutions for application 1 with h = 0.1
|
Mesh values |
Non-uniform order six method [3] |
New uniform order five method |
|
0.01 |
2.317∙10-3 |
1.572∙10-5 |
|
0.05 |
3.014∙10-3 |
1.576∙10-5 |
|
0.08 |
2.908∙10-3 |
9.105∙10-5 |
|
0.10 |
2.001∙10-4 |
5.676∙10-5 |
|
0.11 |
1.534∙10-4 |
4.744∙10-5 |
|
0.15 |
4.810∙10-4 |
4.481∙10-7 |
|
0.18 |
3.591∙10-4 |
2.194∙10-5 |
|
0.20 |
5.413∙10-5 |
1.536∙10-5 |
|
0.21 |
8.751∙10-7 |
1.255∙10-5 |
|
0.25 |
7.497∙10-5 |
2.766∙10-6 |
|
0.28 |
4.395∙10-5 |
4.271∙10-6 |
|
0.30 |
1.098∙10-5 |
3.118∙10-6 |
|
0.31 |
2.955∙10-6 |
1.757∙10-8 |
|
0.35 |
1.028∙10-5 |
2.492∙10-6 |
|
0.38 |
4.393∙10-6 |
1.683∙10-6 |
|
0.40 |
2.578∙10-6 |
1.884∙10-6 |
|
0.41 |
1.274∙10-6 |
5.469∙10-9 |
|
0.45 |
1.972∙10-6 |
5.239∙10-8 |
|
0.48 |
5.551∙10-7 |
3.107∙10-8 |
|
0.50 |
4.188∙10-7 |
1.968∙10-8 |
Table 2. Absolute errors of numerical solutions for application 5.2 with h = 0.1
|
Mesh values |
Non-uniform order six method [3] |
New uniform order five method |
|
0.01 |
8.831∙10-8 |
4.634∙10-12 |
|
0.05 |
1.094∙10-7 |
1.833∙10-11 |
|
0.08 |
8.695∙10-8 |
4.726∙10-11 |
|
0.10 |
1.474∙10-11 |
5.498∙10-11 |
|
0.11 |
9.761∙10-8 |
6.838∙10-11 |
|
0.15 |
1.210∙10-7 |
4.945∙10-11 |
|
0.18 |
9.610∙10-8 |
7.978∙10-11 |
|
0.20 |
4.040∙10-11 |
7.472∙10-11 |
|
0.21 |
1.078∙10-7 |
6.794∙10-11 |
|
0.25 |
1.337∙10-7 |
5.594∙10-11 |
|
0.28 |
1.061∙10-7 |
8.039∙10-11 |
|
0.30 |
7.186∙10-11 |
8.186∙10-11 |
|
0.31 |
1.192∙10-7 |
1.377∙10-11 |
|
0.35 |
1.478∙10-7 |
6.380∙10-11 |
|
0.38 |
1.173∙10-7 |
9.709∙10-11 |
|
0.40 |
5.920∙10-11 |
9.666∙10-11 |
|
0.41 |
1.317∙10-7 |
8.510∙10-11 |
|
0.45 |
1.633∙10-7 |
7.393∙10-11 |
|
0.48 |
1.297∙10-7 |
1.033∙10-11 |
|
0.50 |
3.286∙10-11 |
1.058∙10-11 |
Table 3. Absolute errors of numerical solutions for application 3 with h = 0.1
|
Mesh values |
Non-uniform order six method [3] |
New uniform order five method |
|
0.01 |
3.927∙10-12 |
7.609∙10-12 |
|
0.05 |
4.953∙10-8 |
8.092∙10-12 |
|
0.08 |
3.998∙10-8 |
2.705∙10-12 |
|
0.10 |
1.937∙10-12 |
2.875∙10-12 |
|
0.11 |
3.559∙10-8 |
7.170∙10-12 |
|
0.15 |
4.482∙10-8 |
7.049∙10-12 |
|
0.18 |
3.618∙10-8 |
2.711∙10-12 |
|
0.20 |
3.522∙10-12 |
5.208∙10-12 |
|
0.21 |
3.220∙10-8 |
6.745∙10-12 |
|
0.25 |
4.055∙10-8 |
6.130∙10-12 |
|
0.28 |
3.273∙10-8 |
2.691∙10-12 |
|
0.30 |
4.781∙10-12 |
7.068∙10-12 |
|
0.31 |
2.913∙10-8 |
6.337∙10-12 |
|
0.35 |
3.670∙10-8 |
5.322∙10-12 |
|
0.38 |
2.962∙10-8 |
2.651∙10-12 |
|
0.40 |
5.769∙10-12 |
8.523∙10-12 |
|
0.41 |
2.636∙10-8 |
5.959∙10-12 |
|
0.45 |
3.321∙10-8 |
4.898∙10-12 |
|
0.48 |
2.680∙10-8 |
4.295∙10-12 |
|
0.50 |
6.525∙10-12 |
2.241∙10-12 |
Conclusion
In this work we selected the Gauss points for both interpolation and collocation to avoid the introduction of an extra equation see [8] to enhance the stage order of the Gauss-Runge-Kutta method. However, it is well known from [2] and [5] that the choice of Gauss points for collocation leads to a family of Runge-Kutta schemes with highest order of accuracy, maintains the characteristic of symmetry and strong property of algebraic stability of the method.
From the forgoing tables above we see that the new symmetric method performs remarkably well for both stiff and non-stiff problems. For the uniformity of orders in addition to equation (3.3) we have evaluated the solutions of the three applications at all the off-step points u, w, v and at the step point xn+1 as shown in the tables above.
References
1. Ascher U., Bader G., Stability of collocation at Gaussian points, Society for Industrial and Applied Mathematics, J. Numer. Anal., 1986, 23(2), p. 412-422.
2. Burrage K., Butcher J. C., Stability criteria for implicit Runge-Kutta methods, SIAM J.Numer. Anal., 1979, 16, p. 46-57.
3. Butcher J. C., The Numerical Analysis Of Ordinary Differential Equations: Runge-Kutta and General Linear Methods, John Wiley and Sons, pp. 209-237, 1987.
4. Butcher J. C., Cash J. R., Towards efficient Runge-Kutta methods for stiff systems, SIAM. J. Numer. Anal., 1990, 27(3), p. 753-761.
5. Hairer E., Wanner G., Characterization of non-linearly stable implicit Runge-Kutta methods, Lecture Notes in Mathematics, 1982, 968, p. 207-219.
6. Sarafyan D., New algorithms for continuous approximate solution for ordinary differential equations and upgrading of the order of the processes, Comp. Math. Applic., 1990, 20(1), p. 77-100.
7. Onumanyi P., Awoyemi D. O., Jator S. N., Sirisena U. W., New linear Multi-step methods with continuous coefficients for first order initial value problems, Journal of the Nigerian Mathematical Society, 1994, 13, p. 37-51.
8. Yakubu D. G., Onumanyi P., Sirisena U. W., Garba E. J. D., A new uniform order six one–step Runge-Kutta method, International Journal of Computational and Applied Mathematics, 2006, Submitted.
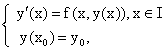
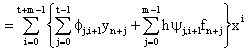
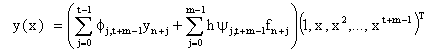

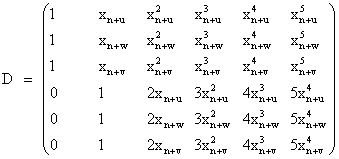
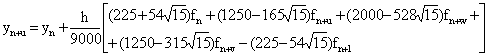
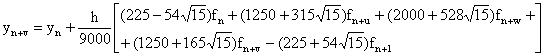 order p = 5, C6 = 6.94 ×
10-7
order p = 5, C6 = 6.94 ×
10-7