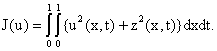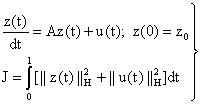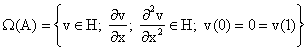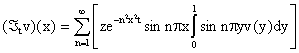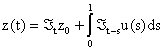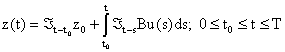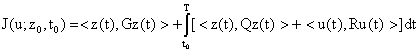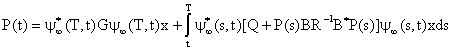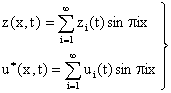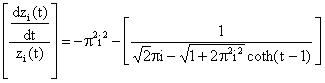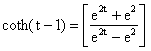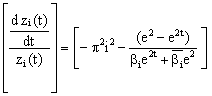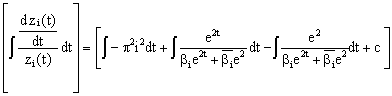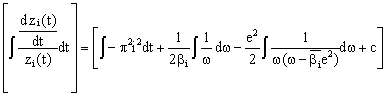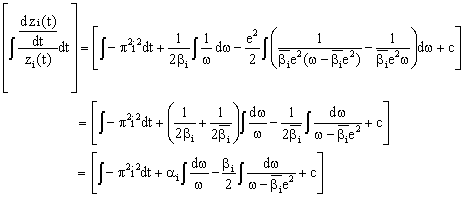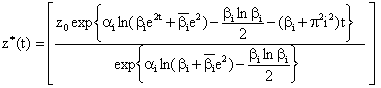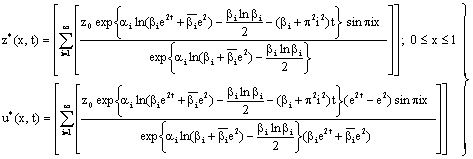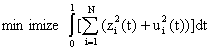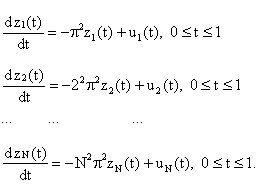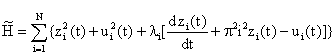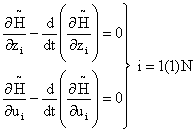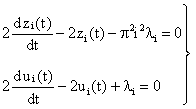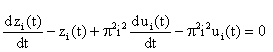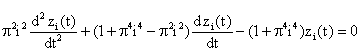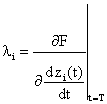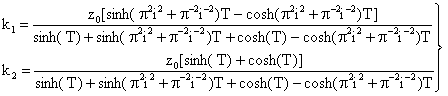A Solution Technique for Solving Control Problems of Evolution Equations

Mathew. A. IBIEJUGBA and Oludayo O. OLUGBARA

Department of Computer and Information Technology, Covenant University, Ota, Nigeria

maibiejugba@yahoo.com, oluolugbara@gmail.com

Abstract

A new optimal solution technique for solving the control problem for evolution equations is established. Since it is well known from empirical studies established in theory that the rate of convergence of most penalty function methods deteriorates as the penalty constant tends to infinity in an attempt to meet the requirement for closer constraint satisfaction, a semigroup based technique is what we find as a convenient tool to confirm this result. Furthermore, we use the Euler-Lagrange technique to provide a basis for comparison of our results. Our findings are quite comparable with the results obtained from the Euler-Lagrange analysis.

Keywords

Evolution Equations; Quadratic Cost Control Problems; Semigroup; Riccati Equation; Euler-Lagrange Equations

Introduction

In our earlier publication [1], we applied the finite-element method for solving the control of a diffusion equation:

(1)

with boundary conditions:

and governed by the initial state:

where we chose the input u(x,t) so as to minimize the quadratic cost functional:

Generally speaking, the finite-element method for the solution of a variety of complicated scientific problems had enjoyed a period of intense activity and stimulation, primarily because of its simplicity in concept and elegance in development. These qualities have led eventually to the growing acceptance of finite-element method as a promising technique equipped with a powerful mathematical basis. It operates on the subdomain principle. This means that the domain of the equation to be solved is usually divided into a number of separate regions or subdomains. The unknown solution function is then approximated in each subdomain by some functions, generally known as pyramid functions or basis functions. To solve this control of a diffusion equation, we now present the derivation of a solution technique, which is based on the semigroup approach.

The Solution Technique

In [2], Curtain and Pritchard presented the following approach. They chose H = L₂[0,1] and took the abstract form of the diffusion equation as:

(2)

where z(t), z₀, u(t)  H, A is a linear operator on the Hilbert space H and

The operator A generates an analytic semigroup  given by:

for all v Î H. The mild solution of Equation (2) is presented as:

which is a special case of the quadratic cost control problem:

where  is a strong continuous semigroup, the admissible controls u Î L₂(t₀, T; H), z₀ Î H and

B Î L (y, H). The problem is to find the optimal control u^* Î L₂(t₀, T; y), which minimizes the quadratic cost function:

where G, Q Î L(y, H) are positive and R Î L(y, H) is strictly positive.

The following results (Theorem 1 and Theorem 2) are then stated and proved in [2]:

Theorem 1

The optimal control, which minimizes J(u; z₀, t₀) is the feedback control

where, P(t) is defined as:

for all x Î H, where y_¥(., .) is the mild operator associated with the operator A-BR^-1B^*P(t).

Theorem 2

P(t) is the unique solution of the following inner product Riccati equation:

on [t₀, T], P(t) = G for x, y Î W(A). By virtues of the results of Theorems 1 and 2 above, the desired optimal control u^* is given by:

where:

(3)

on [0, 1], P(1) = 0, where w, v Î W(A).

In order to solve Equation (3), it must be noted that a complete orthonormal basis for H is  and that if

v Î W (A), then

So from the form of Equation (3), Curtain and Pritchard [2] tried for a solution P(t):

where Pij is a positive definite matrix	(4)

On substituting Equation (4) in Equation (3) and equating corresponding coefficients of like terms, it is obtained that the resulting equation:

has the solution:

Conclusively,

(5)

where:

(6)

To determine z_i(t), we note that at the optimum, the following constraint must be satisfied.

hence, we have that:

(7)

Equation (7) can be rewritten by making use of the following transformation:

(8)

yielding:

(9)

where:

(10)

Integrating Equation (9), we obtain the following integral equation:

(11)

where c is a constant of integration to be determined. The w-transformation given by the following equation will simplify Equation (11). So, we set for the sake of our desired simplicity.

(12)

The resulting expression after transformation is given by the following integral equation:

(13)

To further simplify Equation (13), we apply partial fraction decomposition to the third component of the right-hand-side of the equation to obtain the following:

(14)

Finally, by evaluating Equation (14) and substituting for w using Equation (12), we obtain the following:

(15)

Taking the exponential of Equation (15), we obtain the required solution as follows:

(16)

Next, we determine the constant of integration in Equation (16) by substituting for z_i(0) = z₀ at t = 0 (where z₀ is an arbitrary constant). Therefore, the particular solution is given by:

(17)

The optimum state and control are directly obtained from Equations (5), (6) and (17) as follows:

(18)

For convenience of implementation on a digital computer, Equation (17) is entirely rewritten as follows:

(19)

Euler-Lagrange Equations

In this section, we proceed to obtain the analytical solution of the optimization problem described by Equation (1) using the Euler-Lagrange method and in section 4, we compare the solutions computed by the two methods. By employing the substitution given by Equation (5), the equivalent form of our evolution control problem is the following:

subject to the system of dynamic constraints:

(20)

The Hamiltonian  associated with this problem is given by:

(21)

The constant l_i is the Lagrange multiplier and the Euler-Lagrange equations are given by:

(22)

The following equations are obtained by substituting for Equation (21) in Equation (22).

(23)

By combining Equations (23) and eliminating l_i we have:

(24)

Eliminating u_i(t) and  in Equation (24) by using Equation (20) gives:

(25)

To solve for z_i (t) in Equation (25), we seek a solution of the form:

z_i(t) = e^rt

where r is a constant and we obtain the following auxiliary equation.

(26)

Equation (26) is a quadratic in r and it can be factorized into:

(27)

Equation (27) has two distinct real roots r₁ and r₂ given by:

Hence, the general solution of Equation (25) is given by:

This solution is alternatively written in hyperbolic sine and cosine as follows:

(28)

By using the initial condition z_i(0) = z₀ and the free-end condition [3]:

which translates to z_i(T) = 0. The values of the constants k₁ and k₂ are obtained as follows:

(29)

Finally, the expression for u_i(t) is obtained from Equations (20) and (28) as follows:

(30)

A Computer Based Optimization Experiment

We implemented Equations (6), (17) and (18) on Pentium IV processor PC running under Windows XP. The application program used for simulation is the Microsoft Excel 2002, which is a powerful spreadsheet package that features a set of Mathematical functions and excellent user interface. Several time values are used for the numerical experiment. The values of z₀ and x are both set to 0.5. Different values of N were considered up to 9,000,000 and results show that both z_i^*(t) and u_i^*(t) approach zero as N>39 for all values of t ³ 0.045 (see Figure 1). In fact, our method converges rapidly as t increases.

The analytical results show that the optimal values z^*(x,t) and u^*(x,t) both tend to zero for large N, which verifies the theoretical analysis that as N ® ¥, these values tend to zero, see [1, 4, 5]. In [6], via the extended conjugate gradient method algorithm we examined both the kinetic and diffusive behaviours of the parabolic control problem of integral quadratic cost functional described in this paper. The interested reader shall find further information on considering the References [7-12].

To compare the accuracy of the method presented with the Euler-Lagrange method, Equations (5), (28) and (30) were coded and tested on the computer. We recorded the time t Î [0, 1], the solutions computed by both methods and we took T = 1 in Equation (29). The actual solutions computed by the two methods are summarized in Figures 2 and 3 and our results compare very well with those obtained via the Euler-Lagrange method.

Figure 1. Optimal State and Control

Figure 2. Comparison of Optimal and Euler Methods for State

Figure 3. Comparison of Optimal and Euler Methods for Control

Conclusion

Quite often, the state of a system is not adequately described by an ordinary differential equation. Instead the state can be modeled by differential delay equations, partial differential equations, integral equations or coupled ordinary and partial differential equations.

Many industrial processes using chemical reactors, furnaces, distillation columns for examples are best modeled by partial-integro differential equation and are commonly called distributed parameter systems in engineering parlance.

We have proposed an optimal solution technique for solving the control problem for evolution equations.

Our results are comparable to those obtained via Euler-Lagrange approach.

References

1. Aderibigbe F. M., An Extended Conjugate Gradient Method Algorithm for Evolution Equations,  PhD. Thesis, University of Ilorin, 1987.

2. Curtain R. F., Pritchard A. J., Functional Analysis in Modern Applied Mathematics,  Academic Press, pp. 326-329, 1977.

3. Burghes D., Graham A., Introduction to Control Theory Including Optimal Control, Ellis Horwood Ltd., 1980.

4. Ibiejugba M. A., On the Ritz Penalty Method for Solving the Control of a Diffusion Equation, Journal of Optimization Theory and Applications, 1983, 39(3), p. 431-449.

5. Ibiejugba M. A., Computing Methods in Optimal Control, PhD Thesis, University of Leeds, Leeds, England, 1980.

6. Reju S. A., Ibiejugba M. A., Evans D. J., An Extended Conjugate Gradient Algorithm for the Diffusion Equation, International Journal of Computer Mathematics, 1999, 72, p. 81-99.

7. Ibiejugba M. A., A Penalty Optimization Technique for a Class of Regulator Problems, Part III, Journal of Optimization Theory and Applications, 1990, 64(3), p. 527-546.

8. Ibiejugba M. A., Onumanyi P., A Control Operator and Some of its Applications, Journal of Mathematical Analysis and Applications, 1984, 103, p. 31-47.

9. Ibiejugba M. A., The Role of Penalty Constants in the Convergence of Optimization Problems, Advances in Modelling and Simulation, 1985, 3, p. 27-35.

10. Ibiejugba M. A., The Role of the Multipliers in the Multiplier Method, Journal of Optimization Theory and Applications, 1985, 47, p. 195-216.

11. Ibiejugba M. A., Adeboye K. R., On the Convergence of a Diffusion Equation, Advances in Modelling and Simulation, 1984, 2, p. 47-58.

12. Ibiejugba M. A., Rubio J. E., A Penalty Optimization Technique for a Class of Regulator Problems, Journal of Optimization Theory and Applications, 1988, 58, p. 39-62.