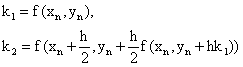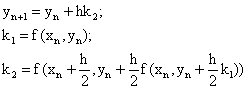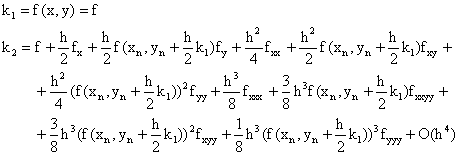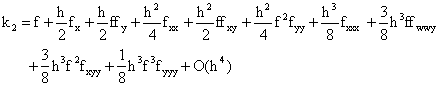Improving the Improved Modified Euler Method for Better Performance on Autonomous Initial Value Problems
Abraham OCHOCHE
Department of Mathematics and Computer Science, Federal University of Technology Minna, Nigeria; E-mail: abochoche@gmail.com
Abstract
The purpose of this paper was to propose a modification that would lead to a much improved approximation technique for the computation of the numerical solutions of initial value problems, particularly the autonomous type. The method that has been improved upon is our Improved Modified Euler method. By the simple modification effected, a much better performance was achieved, not just for the autonomous problem, but for the non-autonomous problem as well. The new method was also shown to be of order 2.
Keywords
Differential Equations; Autonomous; Non-autonomous; Initial Value; Problem; Euler Method; Modified; Improved.
Introduction
In [1], a modified approximation technique for the computation of the numerical solutions of initial value problems (IVP) was proposed. The method was tagged Improved Modified Euler (IME) and the method that was improved upon is the Modified Euler (ME) method. Numerical experiments showed that the new method outperforms the ME method for non-autonomous problems. However, it was observed that the IME method did not do well with regards to autonomous problems and this is the reason for this paper.
The purpose of this paper is therefore to propose a modification of the IME method, to not only improve its ability to handle autonomous problems but its overall performance as well.
Differential equations are one of the most important mathematical tools used in modeling problems in physical sciences. Historically, differential equations (DE) have originated in chemistry, physics and engineering. More recently, they have also arisen in medicine, biology, anthropology, and the like. Ordinary differential equations (ODE) arise frequently in the study of physical systems. Unfortunately, many cannot be solved exactly. This is why the ability to numerically approximate these methods is so important [2].
Numerical solution of ODE is the most important technique ever developed in continuous time dynamics. Since most ODE are not soluble analytically, numerical integration is the only way to obtain information about the trajectory. Many different methods have been proposed and used in an attempt to solve accurately, various types of ODEs All these, discretize the differential system, to produce a difference equation or map.
The methods, obtain different maps from the same equation, but they have the same aim; that the dynamics of the maps, should correspond closely, to the dynamics of the differential equation. [3]
With the advent of computers, numerical methods are now an increasingly attractive and efficient way to obtain approximate solutions to differential equations that had hitherto proved difficult, even impossible to solve analytically.
Generalizations of the Euler Method
Numerical methods for the solution of ordinary differential equations have been developed for over one hundred years. Butcher published a survey paper on this [4]. A classical way of solving initial value problems numerically is by the method of Euler [5].
When Euler proposed his method:
|
|
(1) |
it represented the simplest method available to numerically approximate the solution of an ordinary differential equation.
In the formulation of equation (1) we note that [6]:
- yn+1depends explicitly on yn but on no earlier of yn, yn-1 , …. .
- the function f is evaluated only once in the step from the computation of yn to the computation of yn+1;
- only the function f itself is used rather than f2, f2 , … say which yield values of y’’(x), y’’’(x) in terms of y(x)or of f’ (the Jacobian of f), f’’ …. .
Euler method is both one-step and multi-step, and this fact together with the stability requirements, can mean that h has to be chosen to be very small and as noted in [6], “the method of Euler is ideal as an object of theoretical study but unsatisfactory as a means of obtaining accurate results.”. Due to the low accuracy and poor stability behavior, generalizations have been made to the method of Euler.
The most important generalizations of equation (1) are:
(a) The use of formulae that violate (i). That is, yn+1 depends on yn-1, …, yn-k (k³1) as well as on yn These methods are known as linear multistep methods
(b) The use of formulae that violates (ii). That is more than one evaluation of f is involved in a formula for yn+1. These methods are known as Runge-Kutta methods (and include methods such as mid-point quadrature rule and trapezoidal method).
(c) The use of formulae that violate (iii). For example, expressions for y’’(x), y’’’(x) may be used along with an expression for y’(x)The Taylor series method is an example of such a method. [6]
The notable generalizations of the Euler method are (a) and (b). As Runge [7] observed, Euler’s method give rise to a rather inefficient approximation of the integral by the area of a rectangle of height f(x0). Therefore, he stated that “it is already much better” to extend the Midpoint rule
|
|
(2) |
and the Trapezoidal rule
|
|
(3) |
to differential equations by inserting the forward Euler step for the missing y-values to obtain the Modified Euler method [8]
|
|
(4) |
which we can rewrite as
|
|
where
|
|
and the Improved Euler method
|
|
[which we can also rewrite as
|
|
where
|
|
respectively.
The Improved Modified Euler (IME) Method
As earlier stated, we had achieved an improvement on the Modified Euler method.
We achieved this, by inserting the forward Euler method, in place of yn in the inner function evaluation of the Modified Euler method thus:
|
|
(5) |
We can go on to rewrite it as
|
|
(6) |
with:
|
|
Improving the Improved Modified Euler Method
It has been stated earlier that the IME method performed very poorly in comparison with the ME method, with respect to autonomous IVP. What we are attempting to achieve is a modification to the IME method that would improve its performance.
We had improved upon the ME method by simply inserting the forward Euler Step in place of yn in the inner function evaluation of the ME method. However, we are now attempting an improved modification of our IME method by inserting the entire y component of k2 in the ME method into the inner function evaluation of the IME method, in place of the forward Euler step thus:
|
|
(7) |
Which we can go on to re-write as
|
|
(8) |
Determining the Order of the New Method
In this section the order of the new method (which we will refer to as Modified Improved Modified Euler (MIME) method), would be determined. This will be achieved by first carrying out a Taylor’s series expansion of the slopes (i.e. the krs,(r=1,2)) and then of the exact solution yn+1 As many term as possible in both expansions would then be equated, if we are able to equate terms up to and including o(hq), then the method is of order q [9].
We now proceed to expand the kis,(i=1,2) in turn by Taylor’s theorem [10];
|
|
(9) |
where:
|
|
|
|
(10) |
Without loss of generality, equation (10) can be written as
|
|
(11) |
Collecting like terms in powers of h;
|
|
Adopting the notation also used in used in [10]
Set:
|
|
|
|
(12) |
Substituting our new expressions for k1and k1into equation (8) we obtain
|
|
(13) |
The Taylor series for yn+1is given by
|
|
(14) |
Next, we need to express the total derivatives of y in equation (14) in terms of f and its partial derivatives. Again, from [11] they are as follows:
|
|
(15) |
Slotting (15) into equation (14) we obtain
|
|
(16) |
On comparing the terms in equations (13) and (16) we immediately see that they agree up to and including O(h2) only. From our assertion at the beginning of this section, we can conclude that our new method, is of order 2 i.e. the local error is O(h3).
Numerical Experiments
In this section the new Modified Improved Euler (MIME) method, would be compared with the Modified Euler (ME) method as well as the Improved Modified Euler (IME) method. This would be done by solving the same set of IVP. We recall that our IME method performed dismally in comparison to the ME method with regards to the autonomous IVP. It is hoped that the new MIME method would give a much improved performance.
The IVP we shall be solving are:
i. Problem A1 (the negative exponential) in the DETest problem set [11];
|
|
|
ii. |
Both problems were solved using a constant step size (h) of 0.1.
The results are presented in Figures 1 and 2 respectively below
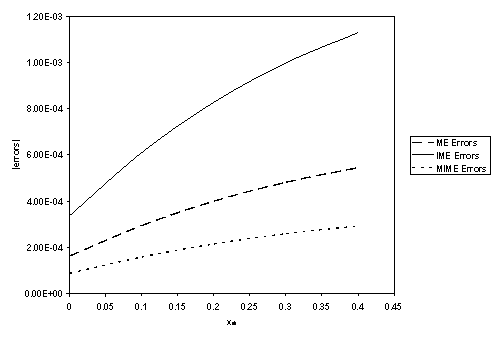
Figure1. Comparing the Modified Euler (ME) method, our Improved Modified Euler
(IME) method and the new Modified Improved Modified Euler (MIME) method for problem i

Figure2. Comparing the Modified Euler (ME) method, our Improved Modified Euler
(IME) method and the new Modified Improved Modified Euler (MIME) method for problem ii
Discussion
The purpose of this paper was primarily to make our Improved Modified Euler method better at handling autonomous IVP. From Figure 1, it is very obvious that this has been achieved. The new MIME method did not only do better than our previous IME method, it also outperformed the ME method. The icing on the cake is problem ii where once again, the new MIME method greatly outperforms both the ME and our IME methods.
Conclusion
In this paper, an attempt has been made to improve the performance of our IME method. It was also shown that the new method, which we tagged as Modified Improved Modified Euler (MIME for short) method is equally of order 2, just like the ME and IME methods. Numerical experiments carried out have shown that not only has the performance of our IME method been improved for autonomous problems, it has been improved overall. The absence of necessary hardware and software constrained the extent of our numerical experiments.
Special Acknowledgements
As always, I want to acknowledge the immense contributions of Prof. John C. Butcher, Emeritus Professor of Mathematics, The University of Auckland, New Zealand, Professor K. R. Adeboye, of the Federal University of Technology Minna, Nigeria, as well as Dr. Nicolette Rattenbury, of the Manchester Metropolitan University, England. They have always challenged and encouraged me and have always been there for me; ready to assist.
References
1. Abraham O., Improving the modified Euler method, Leonardo J. Sci, 2007, 10, p. 1-8.
2. Rattenbury N., Almost Runge-Kutta methods for stiff and non-stiff problems, Ph.D dissertation, The University of Auckland, New Zealand, 2005.
3. Julyan, E. H. C., Piro O., The dynamics of Runge-Kutta methods, Int’l J. Bifur. and Chaos, 1992, 2. 1 – 8.
4. Butcher J. C., Numerical methods for ordinary differential equations in the 20th, Century, J. Comput. Appl. Math., 2000, 125, p. 1-29.
5. Euler H., Institutiones calculi integralis, Volumen Primum (1768), Opera Omnia, Vol. XI, B. G. Teubneri Lipsiae et Berolini, MCMXIII, 1768.
6. Butcher J. C., General linear methods: A survey, Appl. Numer. Math., 1985, 1. 107 – 108.
7. Runge D., Ueber die numerische Auflösung von differentialgleichungen, Math. Ann. 1895, 46, p. 167 – 178.
8. Butcher J. C., and Wanner G., Runge-Kutta methods: some historical notes, Appl. Numer. Math., 1996, 22. 115 – 116.
9. Fatunla S. O., Numerical methods for initial value problems in ordinary differential equations, Academic Press Inc. (London) Ltd. p. 48-51.
10. Abraham O., A fifth-order six stage explicit Runge-Kutta method for the solution of initial value problems, M. Tech Dissertation, Federal University of Technology, Minna, Nigeria, 2004.
11. Hull T. E., Enright, W. H., Fellen, B. M., and Sedgwick, A. E., Comparing numerical methods for ordinary differential equations, SIAM J. Numer. Anal., 1972, 9, 603 – 637.