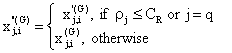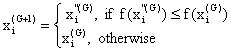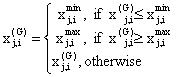Using Evolutionary Computation to Solve the Economic Load Dispatch Problem

Samir SAYAH and Khaled ZEHAR

Department of Electrical Engineering, University of Ferhat Abbas, Setif, Algeria

E-mails: samir_pg04@yahoo.fr, khaledzehar@yahoo.fr

Abstract

This paper reports on an evolutionary algorithm based method for solving the economic load dispatch (ELD) problem. The objective is to minimize the nonlinear function, which is the total fuel cost of thermal generating units, subject to the usual constraints.

The IEEE 30 bus test system was used for testing and validation purposes. The results obtained demonstrate the effectiveness of the proposed method for solving the economic load dispatch problem.

Keywords

Evolutionary Computation; Differential Evolution; Power System Optimization; Economic Load Dispatch.

Introduction

The conventional economic load dispatch (ELD) problem of power generation involves allocation of power generation to different thermal units to minimize the operating cost subject to diverse equality and inequality constraints of the power system. This makes the ELD problem a large-scale highly nonlinear constrained optimization problem.

            It is therefore of great importance to solve this problem as quickly and accurately as possible. Conventional techniques offer good results, but when the search space is nonlinear and has discontinuities, these techniques become difficult to solve with a slow convergence ratio and not always seeking to the global optimal solution. New numerical methods are then needed to cope with these difficulties, specially, those with high speed search to the optimal and not being trapped in local minima. 

            The ELD problem has been solved via many traditional optimization methods, including: Gradient-based techniques, Newton methods, linear programming, and quadratic programming. Most of these techniques are not capable of solving efficiently optimization problems with a non-convex, non-continuous, and highly nonlinear solution space.

In recent years, new optimization techniques based on the principles of natural evolution, and with the ability to solve extremely complex optimization problems, have been developed. These techniques, also known as evolutionary algorithms, search for the solution of optimization problems, using a simplified model of the evolution process found in nature [1]. Differential Evolution (DE) is one of these recently developed evolutionary computation techniques [2, 3]. Differential evolution improves a population of candidate solutions over several generations using the mutation, crossover and selection operators in order to reach an optimal solution. Differential evolution presents great convergence characteristics and requires few control parameters, which remain fixed throughout the optimization process and need minimum tuning [4].

In this paper, a differential evolution based technique is presented and used to solve the ELD problem under some equality and inequality constraints. An application was performed on the IEEE 30 bus – 6 generators test system. Simulation results confirm the advantage of computation rapidity and solution accuracy.

The Economic Load Dispatch Problem

The classical economic dispatch problem is an optimization problem that determines the power output of each online generator that will result in a least cost system operating state. The ELD problem can then be written in the following form:

Minimize           f(x)                                                                                           (1)

Subject to:        g(x) = 0                                                                                    (2)

                        h(x) £ 0 (3)

f(x) is the objective function, g(x) and h(x) are respectively the set of equality and inequality constraints. x is the vector of control and state variables.

Objective function

The objective of the ELD is to minimize the total system cost by adjusting the power output of each of the generators connected to the grid. The total system cost is modeled as the sum of the cost function of each generator (1). The generator cost curves are modeled with smooth quadratic functions, given by:

[$/h]

(4)

where ng is the number of online thermal units, P_gi is the active power generation at unit i and a_i, b_i and c_i are the cost coefficients of the i^th generator.

Equality constraints

The equality constraint is represented by the power balance constraint that reduces the power system to a basic principle of equilibrium between total system generation and total system loads. Equilibrium is only met when the total system generation () equals the total system load (P_D) plus system losses (P_L) as it is shown in (5).

(5)

The exact value of the system losses can only be determined by means of a power flow solution. The most popular approach for finding an approximate value of the losses is by way of Kron’s loss formula (6), which approximates the losses as a function of the output level of the system generators.

(6)

Inequality constraints

Generating units have lower (P _{gi min}) and upper (P _{gi max}) production limits, which are directly related to the design of the machine. These bounds can be defined as a pair of inequality constraints, as follows:

(7)

Overview of Differential Evolution Algorithm

The differential Evolution algorithm (DE) is a population based algorithm like genetic algorithm using the similar operators; crossover, mutation and selection. The main difference in constructing better solutions is that genetic algorithms rely on crossover while DE relies on mutation operators. This main operation is based on the differences of randomly sampled pairs of solutions in the population.

            The algorithm uses mutation operation as a search mechanism and selection operation to direct the search toward the prospective regions in the search space. The DE algorithm also uses a non uniform crossover that can take child vector parameters from one parent more often than it does from other. By using the components of the existing population members to construct trial vectors, the recombination (crossover) operator efficiently shuffles information about successful combinations, enabling the search for a better solution space.

DE optimization process

An optimization task consisting of D parameters can be presented by a D-dimensional vector. In DE, a population of N_P solution vectors is randomly created at the start. This population is successfully improved over G generations by applying mutation, crossover and selection operators, to reach an optimal solution [3, 4]. The main steps of the DE algorithm are given bellow:

Initialization

Evaluation

Repeat

Mutation

Crossover

Evaluation

Selection

Until (Termination criteria are met)

Mutation

The mutation operator creates mutant vectors  by perturbing a randomly selected vector x_a with the difference of two other randomly selected vectors x_b and x_c,

, i=1, …, NP

(8)

where x_a, x_b and x_c are randomly chosen vectors among the N_P population, and a ≠ b ≠ c. x_a, x_b and x_c are selected anew for each parent vector. The scaling constant F is an algorithm control parameter used to adjust the perturbation size in the mutation operator and improve algorithm convergence.

Crossover

The crossover operation generates trial vectors x_i^’’ by mixing the parameters of the mutant vectors x_i^’ with the target vectors x_i according to a selected probability distribution,

(9)

where i=1, …, N_P and j=1,…, D; q is a randomly chosen index {1,…,N_p} that guarantees that the trial vector gets at least one parameter from the mutant vector; ρ_j s a uniformly distributed random number within [0 , 1] generated anew for each value of j. The crossover constant C_R is an algorithm parameter that controls the diversity of the population and aids the algorithm to escape from local minima. x_j,i^‘(G) and x_j,i^”(G) are the j^th parameter of the i^th target vector, mutant vector, and trial vector at generation G, respectively.

Selection

The selection operator forms the population by choosing between the trial vectors and their predecessors (target vectors) those individuals that present a better fitness or are more optimal according to (10).

(10)

i=1, …, N_P.

This optimization process is repeated for several generations, allowing individuals to improve their fitness as they explore the solution space in search of optimal values.

            DE has three essential control parameters: the scaling factor (F), the crossover constant (C_R) and the population size (N_P). The scaling factor is a value in the range [0, 2] that controls the amount of perturbation in the mutation process. The crossover constant is a value in the range [0, 1] that controls the diversity of the population. The population size determines the number of individuals in the population and provides the algorithm enough diversity to search the solution space.

Control parameter selection

Proper selection of control parameters is very important for algorithm success and performance. The optimal control parameters are problem specific. Therefore, the set of control parameters that best fit each problem have to be chosen carefully. The most common method used to select control parameters is parameter tuning. Parameter tuning adjusts the control parameters through testing until the best settings are determined. Typically, the following ranges are good initial estimates: F = [0.5, 0.6], C_R = [0.75, 0.90], and N_P = [3*D, 8*D] [5].

            In order to avoid premature convergence, F or N_P should be increased, or C_R should be decreased. Larger values of F result in larger perturbations and better probabilities to escape from local optima, while lower C_R preserves more diversity in the population thus avoiding local optima.

Constraint handling

Since most evolutionary algorithms such as differential evolution were originally conceived to solve unconstrained problems, various constraint-handling techniques have been developed. One possible strategy is to generate and keep control variables in the feasible region as follows [6]:

(11)

i=1, …, N_P and j=1,…, D.

where x_j,i^min and x_j,i^max are the lower and upper bounds of the j^th decision parameter, respectively.

Penalty functions can be used whenever there are violations to some equality and/or inequality constraints [7]. Basically, the objective function f(x) is substituted by a fitness function f’(x) that penalizes the fitness whenever the solution contains parameters that violate the problem constraints,

(12)

In this paper, the exterior penalty function method is applied to the equality constraints [7]. The new objective function is than given by

(13)

where K_i is a positive constant number, reflecting the constraint weight. The specification of these weighting factors depends on how strongly we feel about satisfying the constraints.

Test Problem and Results

The economic load dispatch (ELD) problem was solved using the differential evolution (DE) algorithm. The simulation was performed on the IEEE 30 bus – 6 generators test system described in [8]. Table 1 shows the data for the six generators.

The parameters used for the DE algorithm are presented as follows:

· Scaling factor (F) was set to 0.70, the crossover constant (C_R) to 0.99 and the population size (N_P) to 26. The load was set to 2.834 pu on a 100 MVA base. The penalty factor (K) of the equality constraint was set to 5×10⁵.

To demonstrate the effectiveness of the DE algorithm, two different cases were considered as follows (see Table 1):

Table 1. Generators Data of the IEEE 30 Bus Test System

	Gen. 1	Gen. 2	Gen. 3	Gen. 4	Gen. 5	Gen. 6
a [$/h]	0	0	0	0	0	0
b [$/MWh]	2.00	1.75	1.00	3.25	3.00	3.00
c [$/Mw^2 h]	0.00375	0.0175	0.0625	0.00834	0.025	0.025
Pgmin (MW)	50	20	15	10	10	12
Pgmax (MW)	200	80	50	35	30	40

Case (1)

The system is considered as lossless and only the generation capacity constraints are considered. The results obtained with the DE algorithm are shown in Table 2. The variation of the total fuel cost function during the optimization process is shown in Fig. 1. The convergence was obtained with 0.34 seconds and 85 generations.

The results of the proposed approach were compared to those using the conventional Newton’s method [9]. Comparison results are given in Table 2. From this table, it can be seen that DE algorithm gives a comparable solution than Newton method.

Table 2. Simulation Results without losses (Case 1)

Parameters	Newton	DE
Pg1 (MW)	185.400	184.095
Pg2 (MW)	46.872	47.301
Pg3 (MW)	19.124	18.842
Pg4 (MW)	10.000	10.866
Pg5 (MW)	10.000	10.179
Pg6 (MW)	12.000	12.116
Total generation (MW)	283.40	283.40
Cost ($/h)	767.60	767.78
CPU time (sec.)	0.09	0.34

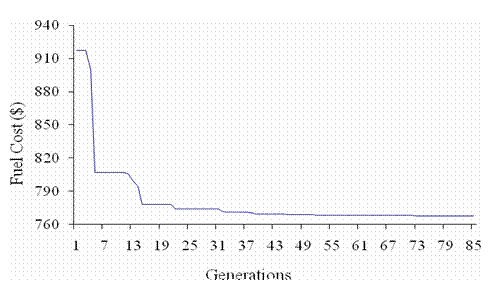
Figure 1. Convergence of the fuel cost function (case 1)

Case (2)

In this case, the transmission power loss has been taken into account. Convergence of the total fuel cost function is shown in Fig. 2. The results obtained with the DE algorithm were compared to those reported using gradient projection method (GPM) [8], successive linear programming (SLP) [10], Quasi-Newton (QN) [11] and genetic algorithm (GA) [11]. The comparison results are summarized in Table 3.

Table 3. Simulation Results with losses (Case 2)

Parameters	GPM [8]	SLP [10]	QN [11]	GA [11]	DE
Pg1 (MW)	187.22	175.25	170.24	179.37	177.51
Pg2 (MW)	53.78	48.34	44.95	44.24	48.61
Pg3 (MW)	16.95	21.21	28.90	24.61	20.91
Pg4 (MW)	11.29	23.60	17.48	19.90	21.64
Pg5 (MW)	11.29	12.25	12.17	10.71	12.47
Pg6 (MW)	13.35	12.33	18.47	14.09	12.02
Total Generation (MW)	293.88	292.98	292.21	292.92	293.16
Loss (MW)	10.49	9.57	8.80	9.52	9.79
Cost ($/h)	804.85	803.08	807.78	803.69	803.07
CPU time (sec.)	4.32	1.12	n/a	7.00	0.73

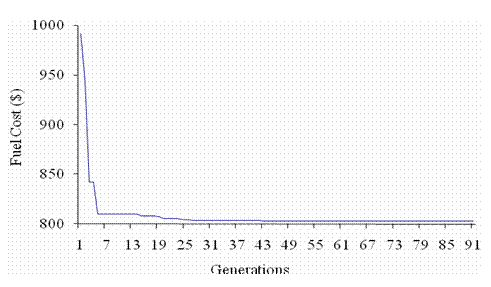
Figure 2. Convergence of the fuel cost function (case 2)

From the results it is clear that DE approach gives the best global optimum solution with less computation time than the other techniques. The results clearly show the ability of DE algorithm to provide a fast global optimum solution.

Conclusions

In this paper, an evolutionary algorithm was applied to solve the economic load dispatch problem. Simulation results demonstrate the ability of the DE-based technique to solve efficiently the ELD problem. The approach was tested on the IEEE 30-bus 6-generators system. The results were compared with those obtained from other optimization techniques and has been found to obtain the global optimum solution with less computation time.

Penalty strategy selection for constraint handling is very important for the success and performance of DE algorithm. The use of static or constant penalties is not suitable for all constraints, but improves computational resources since they require less floating point operations than dynamic penalties.

            A correct set of control parameters such as the scaling factor, crossover constant and sufficient members may lead to very successful results in reasonable computational time.

References

1. Wong K. P., Yuryevich J., Optimal power flow method using evolutionary programming, Springer-Verlag Berlin, 1999, p. 405-412.

2. Price K., Differential Evolution: a fast and simple numerical optimizer, Biennial Conference of the North American Fuzzy Information Processing Society NAFIPS, 19-22 June 1996, p. 524-527.

3. Storn R., On the usage of differential evolution for function optimization, Biennial Conference of the North American Fuzzy Information Processing Society NAFIPS, 19-22 June 1996, p. 519-523.

4. Storn R., Price K., Differential Evolution – a simple and efficient adaptive scheme for global optimization over continuous spaces, Journal of Global Optimization, 1997, 11, p. 341-359.

5. Pérez-Guerrero R. E., Cedeño-Maldonado J. R., Differential Evolution based economic environmental power dispatch, in Proceedings of the 37th Annual North American Power Symposium, 23-25 October 2005, p. 191-197.

6. Lampinen J., A constraint handling approach for the differential evolution algorithm, Proceedings of the 2002 congress on evolutionary computation, CEC ’02, 2002, 2,p. 1468-1473.

7. Chong E. K. P., An introduction to optimization, John Wiley & Sons, Inc., New York, 2001.

8. Lee K.Y., Park Y.M., A united approach to optimal real and reactive power dispatch, IEEE Transactions on Power Apparatus and Systems, 1985, PAS-104(5), p. 1147-1153.

9. Wood J., Wollenberg B. F., Power generation operation and control, John Wiley & Sons, 1984.

10. Sayah S., Zehar K.,  Bellaouel N., A successive linear programming based method for solving the optimal power flow problem, Proceedings of the first international meeting on Electronics & Electrical Science and Engineering, IMESE’06, November 4-6, 2006, University of Djelfa, Algeria.

11. Bouktir T., Slimani L., A genetic algorithm for solving the optimal power flow problem, Leonardo J. Sci., 2004, 4, p. 44-58.