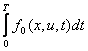Optimal Control Strategies in a Two Dimensional Differential Game Using Linear Equation under a Perturbed System

Musa Danjuma SHEHU

Department of Mathematics/Computer Science, Federal University of Technology, Minna, Nigeria

E-mail: Shehumusa_23@yahoo.com

Abstract

This paper lays emphasis on formulation of two dimensional differential games via optimal control theory and consideration of control systems whose dynamics is described by a system of Ordinary Differential equation in the form of linear equation under the influence of two controls U(.) and V(.).  Base on this, strategies were constructed.  Hence we determine the optimal strategy for a control say U(.) under a perturbation generated by the second control V(.) within a given manifold M.

Keywords

Hamiltonian; Manifold; Saddle point; Control System; Linear equation.

Introduction

      The study of differential games was initiated by Rufus Isaacs in the early 1950’s. In his pioneering work, Isaac tacitly assumed that the notion of strategy had been defined, that a saddle point existed and that the game had a continuously differentiable function [1]. The natural extension of both discrete and continuous games into the dynamic case yield what is known as differential game [2]. Basically a differential game is a mathematical model designed to solve a conflicting situation that changes with time.  A strategy é for control U is a sequence of instructions ( é_n ) and a strategy D for control V is a sequence of instructions (D_n).

      The saddle point condition

P(t,x,u,v*) < P(t,x,u*,v*) < P(t,x,u*,v)

(1)

Suggested that if the game had a value for every initial (t,x) and if a saddle point existed; then the optimal trajectories would be solutions of a minimum and maximum problem in the calculus of variations.

Statement of Optimal Control Problem

We consider a problem of the following form;

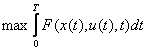
            The basic optimal control problem can be stated as [3]:

Find the control vector U through

which minimizes the functional called the performance index

J =	(2)

; is called the state vector; t is the time parameter, T is the terminal time and f₀ is a function of x, u, and t

            The state variable X_i and the control variables U_i are related as;

dx_i/dt = f_i(x₁, x₂………x_n; u₁, u₂……u_m: t),    i=1,2…..n

That is,

x^- = f(x, u, t)

(3)

The statement of optimal control theory as explained above is important tools in the derivation of the necessary conditions for the solution of Differential games. Necessary conditions for Differential games can be derived through the optimal control using the following problem.

            Find u that minimizes

J =

(4)

            Subject to

= f(x, u, v, t)

(5)

With the boundary condition X (0) = k₁

            We first consider the Euler-Lagrange equations given as [4]

d^2/dx^2(∂F/∂ui^’’)- d/dx(∂F/∂ui^’) + (∂F/∂ui)= 0

(6)

            To solve the above control problem we introduce a Lagrange multiplier λ and define an augmented functional J* as

J* =       + λ [f(x, u, t) – )]dt

(7)

            Since the integrand

F = f0 + λ(f – )

(8)

is a function of the variables X and U.

            We can write the Euler-Lagrange equations [with u₁ = x, u₁^’ = ∂x/∂t = , u₂ = u and u₂^’ = ∂u/∂t = ] in equation (6) as; we first take ∂f/∂u_i - d/dx (∂F/∂) = 0 from (6)

            Therefore, ∂f/∂u₁ - d/dx (∂f/∂ u_i^’) = 0

            We then have ∂f/∂x - d/dt (∂f/∂) = 0

where u_i^’ = ∂x/∂t =

Therefore,

∂f/∂u1 - d/dx(∂f/∂ u1^’) =0 = ∂f/∂x – d/dt(∂f/∂x) =0

(9)

            Similarly,

∂f/∂u₂ - d/dx (∂f/∂) =0

            We have

∂f/∂u - d/dt(∂f/∂) = 0

(10)

where  = ∂u/∂t =

            In view of relation (8), equation (9) can be expressed as

∂f0/∂x + λ ∂f/∂x + = 0

(11)

where  = ∂λ/∂t

            That is, λ() from the relation

F = f₀ + λ (f – ) = ∂λ/∂x x ∂x /∂t

where ∂ x/∂t= x, ∂λ/∂t =

            Similarly, we have

∂f/∂u + λ ∂f/∂u = 0

(12)

            That is from the relation

F = f₀ + λ (f –) and equation (10)

We define a new functional H called the Hamiltonian functional as

H = f0 + λf

(13)

            From equation (11), that is, ∂f₀/∂x + λ ∂f/∂x +  = 0

            We set f₀ = H – λf from equation (13). That is,

∂f0/∂x = ∂H/∂x - λ ∂f/∂x = 0

(14)

            Substituting equation (13) in equation (11), we have

.

∂H/∂x - λ ∂f/∂x + λ ∂f/∂x +  = 0

∂H/∂x + λ = 0

Þ = - ∂H/∂x

(15)

            Similarly from equation (12)

            That is, ∂f/∂u + λ ∂f/∂u = 0      

            We set f₀ = H - λ f from equation (13). That is,

∂f/∂u = ∂H/∂u - λ ∂f/∂u

(16)

            Substituting equation (16) in equation (12), we have ∂H/∂u - λ ∂f/∂u + λ ∂f/∂u = 0

Þ∂H/∂u = 0    or ∂H/∂v = 0

(17)

            The necessary conditions stated above are important tools in the solution of differential games.

            Optimal control theory is equivalent to a differential game with only one player and control problems can be extended to differential games by adding an opponent.

Statement of Differential Game Problem

Given the dynamic system

= f(x,u,v,t), x(to) = xo

(18)

The terminal constraints are

y(x(tf),tf )= 0

(19)

and the performance criterion is

P=  Ø(x(tf),tf ) +

(20)

            We then find u^o and v^o such that

P(u^o , v) ≤ P(u^o , v^o) ≤ P(u ,v^o)

(21)

Saddle Point Property for Differential Game Problems

The saddle point property of differential games can be visualized as follows:      

We have a Hamiltonian function as defined in equation (13) as;

H^ouu  ≥ 0,   H^ovv ≤ 0

(22)

or alternatively

H(x,λ,t) = min max H(x,λ,u,v,t), uєU vєV for P(u^o,v^o) = min P(u,v^o)             u	(23)
Where v^o = v(t;xo,to)	(24)

And similarly for

P(u^o,v^o) = max P(u^o,v)                    v   where u^o = u(t;xo,to)

(25)

            To establish the saddle point we must show that u^o, v^o in (3.7) and (3.8) are the same.

Solution Strategy by Equation of Motion

            Let x(t) be an n-dimensional phase vector which indicates the state of the controlled system at time t.  Its dynamics is described by a system of n differential equations [5-6];

dx(t)/dt = f(t, x(t), u(t), v(t) )

(26)

with initial condition

x(to) = xo

(27)

u(t) is a p-dimensional vector which characterizes the controlling action at time t. The w-dimensional vector v(t) correspond to the disturbance acting at time t.

Besides,

u(t) UÌR^p ;  v(t)V Ì R^q

(28)

Where U and V are compact sets.  Vectors u(t) and v(t) are called controls for u-player and v-player respectively.

            It will be assumed that u(.) and v(.) are measurable functions, a condition which in general is necessary for equations (26) and (27) to make sense.

            The game begins at a given x(t_o) and ends when x(t) reaches a given terminal closed manifold.

            Differential games can be formulated in the form of a linear equation where the control system is formulated in form of linear equations [7-8].

            We consider a control system;

	(29)
	(30)

Where ïuï ≤ 1;  ïvï ≤ 1

            Let M be the plane x₁ = 0.  The Hamiltonian results

H = y1x2 - y2x1 + 2y1u + y2v

(31)

being

= - ∂H/∂x1 = y2	(32)
= - ∂H/∂x2 = -y1	(33)

            Now integrating equation (32) and (33) in a periodical form (since the game is a repeated motion) about sine and cosine in a sinusoidal pattern we obtain

y1(t) = k cos(t + )	(34)
y2(t) = - k sin(t + )	(35)

where f is a phase difference and

            k a constant (dimension of length)

            To fix the final condition, we may assume that the final time is 0.

            Let us assume

x₁(0) = 0;  x₂(t)= arbitrary

y₂(0) = 0;    y₁(0) arbitrary i.e.  y₁(0) = 1

We then have by definition;

1 = k cos (0+0) =1 = k cos0; k = 1      -           assuming t=0, f = 0 or π

            Replacing these in equation (3.17) and (3.18), we have

f = 0 or f = π : k = 1

The optimal strategies are:

ū = sgn y(t) = sgn cos t

= sgn cos(t+ π )

(36)

v = -sgn y(t) = sgn sin t

= sgn sin(t+ π )

(37)

            The path equations are as follows:

= x₂+ 2u sgn cos t

=x₂  + 2 sgn cos(t+ π )

 = - x₁+ sgn sin t

= - x₁  + sgn sin (t+ π )

Discussions

            We considered a control system described by a system of ordinary differential equations, we want to determine the best strategy for a control which will assure a definite quality under a perturbed system generated from the opposite side.

We employed the solution strategy of two dimensional differential games using specifically the Hamiltonian principle to arrive at solution strategies, base on this we then finally want to find the best strategy a control will take to counteract the effect from the opposing control.

Conclusion and Recommendation

We now consider which of the two possibilities f = 0 or f = π is better. Just before the ending of the game, that is for t negative small, u tries to accelerate and v to delay the termination. And so the point x must be near the axis x₁ = 0,

            From x₁^’= x₂+ 2u it results that u wants to make x₁ as negative as possible and chooses

u=-1.

            In this case in equation (3.19) it is better to take  ū = sgn cos(t+ π ); that is,

u = cos180

u  = -1;

            It is worth noting that under a control system described by a system of ordinary differential equations, it is necessary to construct a strategy (control) which will assure a definite quality for the process controlled under specified conditions when the system is subject to perturbation or a controlling action from the opposite side. Differential games could also be used to study the problem of system design in which the system is subjected to unknown perturbation (disturbances), and the disturbances are considered to be chosen by player II.  Player I choose the design parameters to give the best possible system performance in the event of the worst possible disturbances.

References

1. Lewin J, Differential Games, Robert E. Publishers, New York, 1994.

2. Hanson Y., Applied Optimal Control, Wiley-Inter Science, New York, 1969.

3. Emilio O. R., Modern Optimal Control, Books/Cole Publishing Company, California, 1989.

4. Francis S., Numerical Analysis, Second Edition, Schaum’s Outline Series, New York, 1989.

5. Jerry B. M, Classical Dynamics of Particles and Systems, Academic Press, NewYork, 1982.

6. Stephen G. P., Physics for Scientist and Engineers, John Wiley & Sons, New York, 1996.

7. Rao S. S., Optimization Theory and Application, Second Edition, Willey Eastern Limited, 1984.

8. Philips D. S., Game theory and strategy, MIT Press Cambridge, 1993.