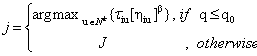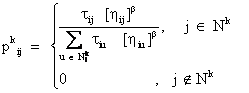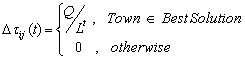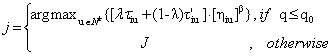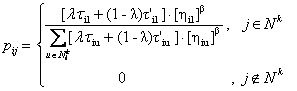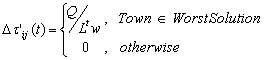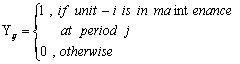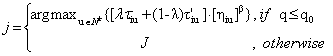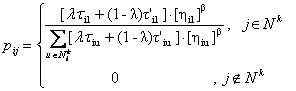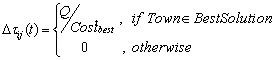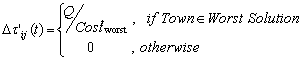Maintenance Scheduling by using the Bi-Criterion Algorithm of Preferential Anti-Pheromone
Triantafyllos MYTAKIDIS and Aristidis VLACHOS
Department of Informatics, University of Piraeus, 80, Karaoli & Dimitriou Str., 18534 Piraeus, Greece
E-mails: T.Mytakidis@gmail.com, AVlachos@unipi.gr
Abstract
This paper presents the solution for the Thermal Generator Maintenance Scheduling Problem, using a bi-criterion Ant Colony Optimization Algorithm called Preferential Anti-pheromone (PAP). This method allows the “agents” of an ant colony to deposit a small amount of pheromone trail to every path that has been used, to construct the potential solutions, but also to give extra emphasis to the best solution found at the end of an iteration of the algorithm. In the same time that good solutions are being investigated from the agents, bad solutions are examined too, with the aim to avoid short-term poor solutions and lead to long-term good and, respectively, global best solutions. In this way, through the iterations of the algorithm, we end up to the final solutions. The algorithm is applied to a real-scale problem, and further investigation is being made so as to find the best possible solution.
Keywords
Thermal Generator; Maintenance Scheduling; Ant Colony Optimization; Ant Colony System; Preferential Anti-Pheromone.
Introduction
The Thermal Generator Maintenance Scheduling Problem is a complex problem that is necessary for the reliability and right operation of a generator system, given that the whole production cost is dependent on the maintenance and operation cost. Thus, the maintenance procedure has to be scheduled and complied with the best possible way, minimizing these two costs and at the same time, covering the energy demands, so as every constraint of the problem is satisfied.
The problem has been studied in the past with a variety of methods and algorithms [1]. The initial formulation was made by Gruhl [2, 3] in 1973. He presented an umbrella of scheduling problems, one of which was the maintenance scheduling problem, with a linear approach.
During 1975, Dopazo and Merill [4] developed a model which was claimed to have the ability of finding the best solution. But this approach was lacking in real-scale problems application, something that Zurn and Quintana [5] later achieved to do.
In 1983, Yamayee and Sidenblad [6] improved the cost function that was used till then, with great improvements in execution time.
Eight years later, Satoh and Nara [7] applied for the first time a stochastic method, called Simulated Annealing with very good results in large-scale systems as well, that were impossible to be solved with linear methods in the past. They also investigated the problem with genetic algorithms [8] and tabu-list methods [9] with similar results, but with the ability to solve real-scale problems, too.
In 1993 Charest and Ferland [10] tried to modify the linear method with successful results in execution time, while Dahal and Donald [11] applied a genetic algorithm in Boolean representation [12] which had also some good results. In 1997, Burke and Smith [13] tried to create a hybrid model of the simulated annealing and the tabu-list method without success, following another attempt to make another hybrid model with memetic and tabu-list methods three years later, which resulted in better results, but with a small increase in execution time.
This paper studies the results of the Anti-pheromone method, an ACS-like algorithm based on the behavior of true ants. It is organized as follows: In section 2, we review the principal framework of the ACO, Ant Colony System and Prefferential Anti-Pheromone methods. In section 3, we represent the formulation of the Maintenance Scheduling problem. In section 4, we represent the implementation of PAP for the problem and the algorithm used. The paper ends with case studies on a real system in section 5 and conclusions in section 6.
Ant Colony Optimization (ACO)
Overview
Ant Colony Optimization is a pack of Artificial Intelligence algorithms that rely on the imitation of the social insects’ behavior, and especially ants’. These algorithms use agents, that we call “ants”, for the investigation of the best solution of a problem, for example the shortest path between some places that might be food for the colony, just like happening with the true ant colonies.
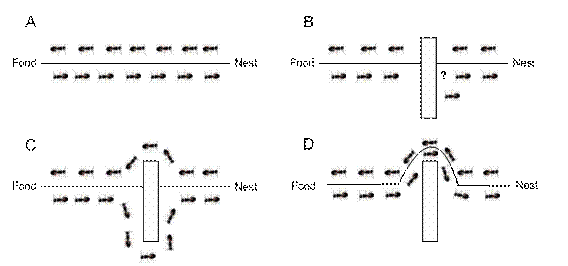
Figure 1. Real ants after a while tend to choose the shortest path between nest and food
These agents, are constructing through iteration the solutions of the problem. The probability for an ant to visit a town is affected from the amount of pheromone that every agent detects during its exploration. Pheromone is a substance that ants produce and deposit along the paths that have traversed, making them more attractive for the next ones that might pass from the same point, while the already existent pheromone is vaporizing as time passes. During the progress of the algorithm, the artificial pheromone is placed after the construction of a complete tour-solution on each and every town that was chosen and visited for the construction of it. In this way, the amount of pheromone is the heuristic information at a given timing point, reflecting the experience of the colony about the feasible solutions of the problem.
If we consider the possible solutions as a graph with the ants moving from town sr to sr+1, then the pheromone level that exists after the passing of an agent from a feasible solution is given from equation:
|
|
(1) |
where:
ñ is the pheromone trail evaporation factor
|
|
n the number of ants
k the number of each ant.
The probability of the kth ant to follow the path from town sr to sr+1, is:
|
|
(2) |
where
Nrk is a feasible solution when ant k is on node r, and arthe action required for the ant to move from node sr+1 tosr.
Ant Colony System (ACS)
The Ant Colony System (ACS) [14] meta-heuristic algorithm belongs to the umbrella of ACO algorithms. On each step of the algorithm (specifically for the Traveling Salesman Problem - TSP, but respectively for other problems), the transition of an ant from town i to town j, depends on:If town has already been visited. For each ant, a tabu list is being saved, which grows each time it reaches a new town, end empties whenever a full solution for the problem is accomplished. In this way, towns are never visited more than once.
The inverse proportion of the distance between two towns
|
|
that is called visibility, and describes the heuristic preference of an ant between two towns.
·
The amount of pheromone ![]() that exists between
two towns i and j, on which the experience of the colony is dependant, and
describes the preference for town j, according to the experience from previous
iterations.
that exists between
two towns i and j, on which the experience of the colony is dependant, and
describes the preference for town j, according to the experience from previous
iterations.
When the kth ant is on town i, the probability to move to town j, is given from equation:
|
|
(3) |
where:
¸ q is a random variable uniformly distributed between [0,1]
¸ q0 is a determining parameter between [0,1]
¸ Nk the number of nodes that are not in tabu list of ant k yet.
J is a town randomly chosen under equation:
|
|
(4) |
where:
¸ â the visibility variable for the transition rule.
¸ Nk the number of nodes that are not in tabu list of ant k yet.
In the end of every iteration the pheromone trail is updated under equation:
|
|
(5) |
where:
¸ t the number of iteration taking place
¸ ñ the evaporation trail factor with 0< ñ < 1
¸
![]() the initial pheromone amount that is
placed on every town.
the initial pheromone amount that is
placed on every town.
After completing an iteration (when all ants have created their won feasible solutions) the global update rule is being applied:
|
|
(6) |
whereã the global pheromone evaporation factor
|
|
where:
¸ Q the amount of pheromone added
¸ Lt the best solution found till iteration t
In this way, the equation above is applied only to towns that belong to the best solution during the execution (all iterations) and this enables them with a bigger amount of pheromone.
Preferential Anti-pheromone
During the ant exploration in the search space, they gain knowledge concerning the most desirable nodes. This often leads to short-term solutions that are not the best ones that can be found. Randal and Montgomery [15] are taking into account this fact with the “Accumulated Experience Ant Colony” - AEAC using a method that can find which solutions can lead to long-term good solutions. Anti-pheromone is a substance that can have similar effects and is placed in nodes that belong to the worst solutions, information that is lost with other methods.
Iradi, Merkle and Middendorf [16] suggest a method called “Preferential Anti-pheromone” (PAP) that uses pheromone, as much as anti-pheromone for the exploration of the search space. The use of this bi-criterion exploration is improved during the iteration process of the algorithm. This improvement is feasible due to the difference of ants concerning their preference between these two kinds of pheromone. For this reason, we use a parameter ë, which is given for the kth ant by equation (k-1)/(m-1), where k=[1,m]. In this way, we give some ants the opportunity to explore the best, but also to some others the worst solutions.
In this way, the transition rule of an ant from town I to town j that we discussed on classical ACO is:
|
|
(7) |
where J is a town chosen by equation:
|
|
(8) |
Pheromone and anti-pheromone are updated in the same way when ants traverse the problem’s nodes to form the solutions, as local updating ignores the cost of solutions produced. So, in addition with the local updating rule of classical ACO for pheromone, anti-pheromone is updated according to the following rule:
|
|
(9) |
After completing a tour and each ant has chosen a feasible solution, pheromone is placed on towns that belong to the best solution according the global updating rule of classic ACS, and pheromone to the worst ones, according to the following rule:
|
|
(10) |
where:
|
|
and Ltw the worst length (cost) solution found on tth iteration.
Formulation of the Problem
The objective of the Thermal Generator Maintenance Scheduling Problem is the maintenance of the energy production units of a system in a given horizon, usually in weeks, with the lowest possible cost.
The list of symbols that describe the problem is as follows [1, 7]:
i : Generator number
É : Number of generators
j : Number of week
J : Horizon in number of weeks
xi: Maintenance start period; xi Î {1, 2, …, J}
Xi: Set of preferred maintenance start periods; Xi: Î {1, 2, …, J}
Mi: : Maintenance length in weeks
Yij: : State variable;
|
|
pij : generator output of unit-i at period-j
fi : fuel cost coefficient (linear cost function)
ci(xi): maintenance cost of unit-i when the maintenance is committed at period xi
Pi : capacity of unit i
Dj : anticipated demand at period-j
Rj : required reserve at period-j
The generator maintenance scheduling problem is formulated as shown below:
Objective function
The objective is to minimize the sum of the following two terms:
|
|
(11) |
where the first term is the production cost and the second is the maintenance cost.
Constraints
1) The nominal starting period of maintenance is pre-specified for each generating unit:
|
|
(12) |
2) Once the maintenance of unit-i starts, the unit must be in the maintenance state for just Mi periods:
|
|
(13) |
3) If unit-i1 and unit-i2 cannot be maintained in a given week because of the crew constraint, the following constraint (combinational constraint) is imposed:
|
|
(14) |
4) If the maintenance of unit-i1 must be finished prior to the starting of that of unit-i2, the following constraint (order constraint) is added:
|
|
(15) |
5) The generator output must be less than its upper limit; and the output of the generator in maintenance must be equal to zero. Such an operation constraint is expressed by:
|
|
(16) |
6) The demand constraint must be met:
|
|
(17) |
7) In order to ensure that the total available power is greater than the demand Dj even when a unit random outage occurs, the reserve constraints are imposed. That is, the total available power from units which are not committed must be greater than the demand plus reserve:
|
|
(18) |
Penalty Function
In the maintenance scheduling problem, the constraints are classified into two groups; “easy” constraints and “difficult” constraints. The easy constraints are eq (2), (3), (5), (6), the difficult constraints are eq (4), (7), (8). Since the set Xi is given, the value of xi can be selected as a member of Xi so that eq (2), (5) are satisfied. Then the value of yij is directly defined by eq (3), and eq (6) becomes a simple bound on pij. On the other hand, it is very difficult to find a feasible solution which satisfies eq (4), (7) and (8). So, the artificial variables zi, ui, and vi are introduced corresponding to eq. (4), (7) and (8), with associated positive penalty parameters á, â, and ã. Then the problem is re-formulated as follows:
|
|
(19) |
|
|
(20) |
|
|
(21) |
|
|
(22) |
|
|
(23) |
|
|
(24) |
|
|
(25) |
|
|
(26) |
|
|
(27) |
|
|
(28) |
By using the above formulation, once the value of xi is determined, the value of yij is directly defined, and the value of pij is calculated through the equal incremental method (equal method) for the economic dispatch problem [1]. Therefore, the value of the objective function can be efficiently evaluated if the value of xi is specified.
Implementation of PAP for the Maintenance Scheduling Problem
Expression approach
For the implementation of the problem, we used a sort of graph. Every node of the graph represents a feasible solution, and more specifically a feasible week that the maintenance of every generator can be started. In this way, every ant traverses one by one the generator units, choosing one of the feasible maintenance starting periods and, in the end, constructing a complete solution. When all ants complete their tours, the iteration is completed and a new one takes place.
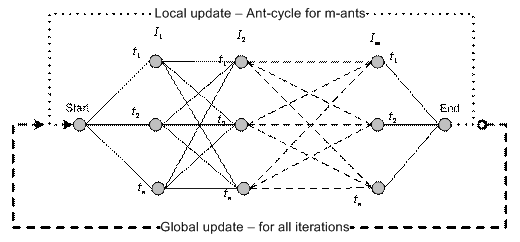
Figure 2. Representation of the problem using graph
So, on every step, all units are selected, and the total cost of the solution is calculated, summing up the total maintenance cost, plus the total generator operation cost needed for every week (plus the penalty of erroneous solutions, if any).
The probability for an ant-k that is on town-i to move to town-j, is given by the random-proportional rule of PAP:
|
|
(29) |
where J is a town chosen by equation:
|
|
(30) |
where Nk are the towns that are not yet included on the kth
agent’s tabu list. As visibility ![]() between towns, we will use the equation
between towns, we will use the equation
|
|
where PCVij(t) is a method counting the total number of the Problem Constraint Violations. We will bias each constraint violation using weights which correspond to the relative importance of each constraint. Thus, the nodes that cause violations will be less desirable by ants.
The pheromone trail is updated every time an ant traverses a node, according to the equation:
|
|
(31) |
where:
t the number of iteration taking place
ñ the pheromone evaporation factor, 0< ñ < 1
![]() the initial amount of pheromone added
on each node
the initial amount of pheromone added
on each node
while the anti-pheromone trail is updated according to the rule:
|
|
(32) |
Finally, the nodes’ pheromone trails that belong to the best solution found are updated according to equation:
|
|
(33) |
where
|
|
and the nodes’ pheromone trails that belong to the worst solution, according to equation:
|
|
where
|
|
where:
ã the global pheromone evaporation factor
Q the amount of pheromone added
Costtbest the best (lowest) cost found till iteration t
Costtworst the worst (highest) cost found on iteration t
The algorithm
1. Define problem parameters for each agent and generator.
2. For every ant and for every generator select a power level randomly.
3. Evaluation of every solution constructed by the ants
Costbest = min { Costbest , Costiteration-best }
Costworst = min { Costworst , Costiteration-worst }
4. Update the amount of pheromone and anti-pheromone trails for every traversed solution (local)
5. Update the amount of pheromone for the best solution path. (global)
6. Update the amount of anti-pheromone for the worst solution path. (global)
7. For every ant and for every generator select a power level based on the random-proportional rule.
8. Repeat algorithm from Step 3
1. Case study on a real-scale system of generators
The algorithm just described, was implemented on a real scale system of generator units [17] with 22 power generator units that have to be maintained within a 52-week horizon.
The table 1 shows the parameters that describe every generator unit’s operation and maintenance.
Table 1. System Parameters
|
É |
|
|
|
|
a |
b |
c |
|
Crew constraint for every maint. week |
|
1 |
100 |
1 |
47 |
6 |
70 |
8.00 |
0.00585 |
0.25 |
10+10+10+5+5+5 |
|
2 |
100 |
1 |
50 |
3 |
70 |
8.00 |
0.00580 |
0.20 |
15+15+15 |
|
3 |
100 |
1 |
50 |
3 |
70 |
8.00 |
0.00580 |
0.20 |
10+15+15 |
|
4 |
100 |
1 |
50 |
3 |
70 |
8.00 |
0.00580 |
0.20 |
10+10+10 |
|
5 |
90 |
1 |
47 |
6 |
60 |
8.00 |
0.00610 |
0.35 |
10+10+10+5+5+5 |
|
6 |
90 |
1 |
49 |
4 |
60 |
8.00 |
0.00610 |
0.30 |
10+10+10+10 |
|
7 |
95 |
1 |
50 |
3 |
68 |
8.00 |
0.00579 |
0.20 |
10+10+10 |
|
8 |
100 |
1 |
49 |
4 |
72 |
8.00 |
0.00565 |
0.20 |
10+10+5+5 |
|
9 |
650 |
27 |
48 |
5 |
525 |
7.00 |
0.00120 |
0.52 |
10+10+10+5+5 |
|
10 |
610 |
6 |
11 |
12 |
510 |
7.20. |
0.00142 |
0.50 |
3+2+2+2+2+2+2+2+2+2+2+3 |
|
11 |
91 |
1 |
49 |
4 |
62 |
8.25 |
0.00600 |
0.20 |
10+10+10+10 |
|
12 |
100 |
1 |
45 |
8 |
74 |
8.15 |
0.00578 |
0.30 |
10+10+5+5+5+5+5+3 |
|
13 |
100 |
1 |
50 |
3 |
70 |
8.00 |
0.00580 |
0.20 |
15+15+15 |
|
14 |
100 |
1 |
47 |
6 |
70 |
8.00 |
0.00585 |
0.25 |
10+10+10+5+5+5 |
|
15 |
220 |
1 |
48 |
5 |
85 |
7.90 |
0.00460 |
0.25 |
10+10+10+10+10 |
|
16 |
220 |
1 |
47 |
6 |
87 |
7.95 |
0.00464 |
0.25 |
10+10+10+5+5+5 |
|
17 |
100 |
1 |
48 |
5 |
69 |
8.18 |
0.00570 |
0.20 |
10+10+10+10+10 |
|
18 |
100 |
1 |
48 |
5 |
69 |
8.17 |
0,00572 |
0.25 |
10+10+10+5+5 |
|
19 |
220 |
1 |
50 |
3 |
81 |
7.90 |
0.00463 |
0.25 |
10+10+10 |
|
20 |
220 |
1 |
50 |
3 |
82 |
7.95 |
0.00462 |
0.25 |
10+15+15 |
|
21 |
240 |
1 |
50 |
3 |
82 |
7.40 |
0.00410 |
0.30 |
15+15+15 |
|
22 |
240 |
1 |
48 |
5 |
80 |
7.42 |
0.00415 |
0.30 |
10+10+10+5+5 |
Table 2. Weekly demand
|
j |
Demand Dj |
j |
Demand Dj |
|
1 |
1694 |
27 |
1737 |
|
2 |
1714 |
28 |
1927 |
|
3 |
1844 |
29 |
2137 |
|
4 |
1694 |
30 |
1927 |
|
5 |
1684 |
31 |
1907 |
|
6 |
1763 |
32 |
1888 |
|
7 |
1663 |
33 |
1818 |
|
8 |
1583 |
34 |
1848 |
|
9 |
1543 |
35 |
2118 |
|
10 |
1586 |
36 |
1879 |
|
11 |
1690 |
37 |
2089 |
|
12 |
1496 |
38 |
1989 |
|
13 |
1456 |
39 |
1999 |
|
14 |
1396 |
40 |
1982 |
|
15 |
1443 |
41 |
1672 |
|
16 |
1273 |
42 |
1782 |
|
17 |
1263 |
43 |
1772 |
|
18 |
1655 |
44 |
1556 |
|
19 |
1695 |
45 |
1706 |
|
20 |
1675 |
46 |
1806 |
|
21 |
1805 |
47 |
1826 |
|
22 |
1705 |
48 |
1906 |
|
23 |
1766 |
49 |
1999 |
|
24 |
1946 |
50 |
2109 |
|
25 |
2116 |
51 |
2209 |
|
26 |
1916 |
52 |
1779 |
where:
¸ Ri the highest level of energy can be produced.
¸ Ei and Li the earliest and latest period that the maintenance can start.
¸ Mi the maintenance period length (in weeks).
¸ a, b, c, the cost parameters for the operation of the generators.
¸ fi the fuel cost coefficient (linear function).
¸ and, finally, the maintenance crew needed for every maintenance week.
The highest level of energy that can be produced from all generators is zero.
The right table, also, represents the anticipated demand of the system for every week within the horizon.
The required reserve for each week of the horizon can be defined using one of the following approaches:
i. As a constant percentage of the demand Dj.
ii. As equal to the size of the largest generating unit.
iii. In dependence of other necessary criteria.
Here, we applied the first approach, with a 20% percentage on demand Dj.
That is: Rj = 20%, Dj , j = 1,2…J
It is important to define some determinant parameters for the solution of the problem. The following executions of the problem are looking into the following matters:
· As we are working on a real system, it is easy to appreciate the fact that we need a maintenance crew constraint that will be:
o “Flexible”, concerning the solutions that can be produced, without confining them.
o Big enough to produce solutions without violations-penalties and, respectively, non-feasible.
o Small enough so as to minimize the existence of not needed crew.
For all these reasons, after close study of the problem constraint table and the solutions produced, the crew number was set to 30.
· As we can see, the objective function describes the constraint violations as extra cost added to the production cost. These solutions are not feasible, thus we have to define the positive penalty weight parameters á, â and ã to be analogous with the solution cost of the problem, so as to be added an extra cost feasible to reject them. After experimental executions, we found that a solution without violations is in the order of hundreds millions cost units (108). So, forasmuch as each violation can occasionally occur, the parameters were defined as follows:
o á = 100
o â = 100
o ã = 20
· The following variables were defined empirically:
o ![]() =0,00001
=0,00001
o Q= 1
o Maximum number of iterations=2000, so as execution is not stopped early, and consequently without a good solution.
o Maximum number of iterations without a better solution=150, number big enough for a decent result.
· The definition of the heuristic information weight parameter â, the local and global pheromone trail evaporation factor ñ and ã, as well as the q0 parameter, is also essential. The following tables represent the results given by experimental executions. All solution costs are indicative and expressed in 108 cost units.
Table 3. â, ñ, q0 and ã versus Best solution
|
â |
Best Cost |
|
ñ |
Best Cost |
|
q0 |
Best Cost |
|
ã |
Best Cost |
|
0.1 |
3.3637 |
|
0.1 |
3.3477 |
|
0.1 |
3.3475 |
|
0.1 |
3.3486 |
|
0.2 |
3.3474 |
|
0.2 |
3.3475 |
|
0.2 |
3.3478 |
|
0.2 |
3.3479 |
|
0.3 |
3.3474 |
|
0.3 |
3.3473 |
|
0.3 |
3.3577 |
|
0.3 |
3.3468 |
|
0.4 |
3.3485 |
|
0.4 |
3.3479 |
|
0.4 |
3.3591 |
|
0.4 |
3.3473 |
|
0.5 |
3.3463 |
|
0.5 |
3.3465 |
|
0.5 |
3.3565 |
|
0.5 |
3.3476 |
|
0.6 |
3.3468 |
|
0.6 |
3.3482 |
|
0.6 |
3.3489 |
|
0.6 |
3.3475 |
|
0.7 |
3.3473 |
|
0.7 |
3.3534 |
|
0.7 |
3.3592 |
|
0.7 |
3.3488 |
|
0.8 |
3.3495 |
|
0.8 |
3.3483 |
|
0.8 |
3.3675 |
|
0.8 |
3.3494 |
|
0.9 |
3.3582 |
|
0.9 |
3.348 |
|
0.9 |
3.3576 |
|
0.9 |
3.3479 |
|
1 |
3.3581 |
|
|
|
|
|
|
|
|
|
|
2 |
3.3591 |
|
|
|
|
|
|
|
|
|
|
3 |
3.3498 |
|
|
|
|
|
|
|
|
|
|
4 |
3.3504 |
|
|
|
|
|
|
|
|
|
|
5 |
3.3485 |
|
|
|
|
|
|
|
|
|
|
6 |
3.3477 |
|
|
|
|
|
|
|
|
|
|
7 |
3.3479 |
|
|
|
|
|
|
|
|
|
|
8 |
3.3479 |
|
|
|
|
|
|
|
|
|
|
9 |
3.3473 |
|
|
|
|
|
|
|
|
|
|
10 |
3.3476 |
|
|
|
|
|
|
|
|
|
|
15 |
3.3486 |
|
|
|
|
|
|
|
|
|
|
20 |
3.3485 |
|
|
|
|
|
|
|
|
|
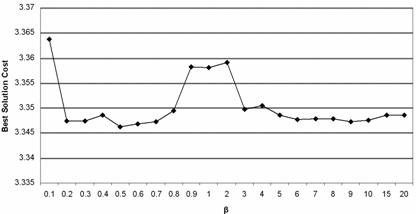
Figure 3. â versus Best solution
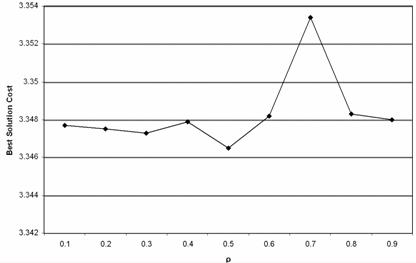
Figure 4 - ñ versus Best solution
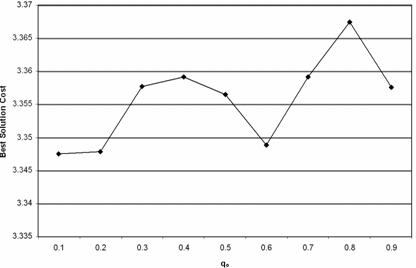
Figure 5. q0 versus Best solution
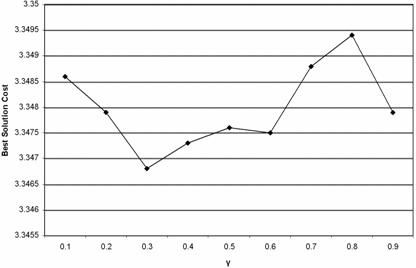
Figure 6. ã versus Best solution
We have to emphasize that the above results are not unique, as randomness is taken into account, although effort was made to minimize this factor.
The following parameters were chosen for the resolution of the problem:
· â=0,5
· ñ=1
· q0=0,6
· ã=0,3
The program of the proposed method is written in Matlab 6.5 and it is run on an AMD Athlon 3000+ 1.79 GHz processor giving the following results:
· The best solution found is
[35,5,36,34,30,19,29,14,46,6,40,7,10,16,25,24,21,26,31,18,48,41]
That is the period that maintenance for every unit of the system can start (For unit 1, maintenance starts at week 35, for unit 2 on week 5, and so on).
· The maintenance periods are represented in detail on the following diagram:
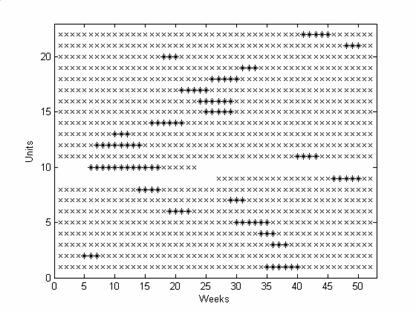
Figure 7. Maintenance periods of Best solution
where the feasible periods are represented with “x” and the selected periods with “*”
· The best solution cost found is 330560000.
· The best solution was found on iteration number 203.
· The best solution progress versus iterations is represented to the following figure:
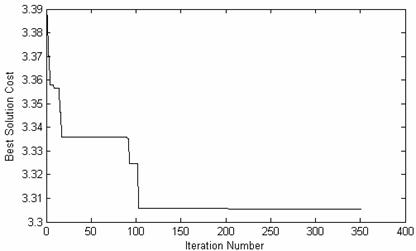
Figure 8. Best solution cost versus Iterations
The execution time is 0:13:35.812.
As we can see in Figure 8, the PAP algorithm has produced a very good solution with only a small number of iterations. From the first steps, it continuously finds better solutions with lower costs, until iteration 203 that no better solution is found for the next 150 iterations, so the algorithm is terminated. It is remarkable that the algorithm produced much better solutions step by step, without being “trapped” on local best solutions due to pheromone trails (a problem that characterizes most ant-based algorithms).
Conclusions
This paper looked into the Thermal Generator Maintenance Scheduling Problem of a real-scale system. The problem has been studied with many mathematical and heuristic approaches in the past. In this project, the preferential Anti-pheromone approach was used, which is a variation of the ACS algorithm based on the behavior of real ant colonies.
The results produced prove that the algorithm can be applied successfully to the problem so as the optimum solutions can be found, even in real energy production systems that the complexity raises significantly, because of the number of generating units, but also due to the number of feasible solutions that have to be produced in a reasonable time interval.
References
1. Burke E. K., Smith A. J., Hybrid Evolutionary Techniques for the Maintenance Scheduling Problem, IEEE Transactions on Power Systems, 2000, 15(1), pp.1-2.
2. Gruhl J., Electric generation production scheduling using a quasioptimal sequential technique, Research Note MIT-EL 73-003, MIT Energy Lab, April 1973.
8. Kim H., Nara K., A method for maintenance scheduling using GA combined with SA, Selected papers from the 16th annual conference on Computers and industrial engineering, 1994, p. 477-480.
15. Randall M., Montgomery J. Q., The Accumulated Experience Ant Colony for the Travelling Salesman Problem, Proceedings of Inaugural Workshop on Artificial Life, Adelaide, Australia, 2001, pp. 79-87.
16. Iredi S., Merkle D., Middendorf M.Q., Bi-Criterion Optimization with Multi Colony Ant Algorithms. Evolutionary Multi-Criterion Optimization, First International Conference (EMO’01), Zuric, 2001, pp. 359-372.
17. Ibrahim El-Amin, Salif Duffuaa, Mohammed Abbas, A tabu search algorithm for maintenance scheduling of generating units, King Fahd University of Petroleum and Minerals, 1998-1999, Electric Power Systems Research 54, 2000, pp. 96.
18. Wood J., Wood B. F., Woolenberg B. F., Power Generation, Operation, and Control, John Wiley, 1984.