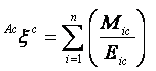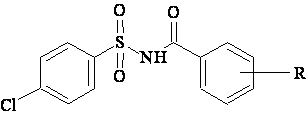Prediction of Antitumor Activity of N-(phenylsulfonyl)benzamides: Computational Approach using Topochemical Descriptors
Harish DUREJA and Anil K. MADAN*
Faculty of Pharmaceutical Sciences, M. D. University, Rohtak-124001, India.
*Corresponding author. E-mail: madan_ak@yahoo.com
Abstract
In the present study, the relationship between the topochemical indices and antitumor activity of N-(phenylsulfonyl)benzamides analogues has been studied. Three topochemical indices, Wiener’s topochemical index - a distance-based topochemical descriptor, molecular connectivity topochemical index - an adjacency-based topochemical descriptor and augmented eccentric connectivity topochemical index - an adjacency-cum-distance based topochemical descriptor, were used for the present investigation. The values of the Wiener’s topochemical index, molecular connectivity topochemical index and augmented eccentric connectivity topochemical index for each of the 62 analogues comprising the data set were computed using an in house computer program. Resultant data was analyzed and suitable models were developed after identification of the active ranges. Subsequently, an activity was assigned to each analogue involved in the dataset using these models, which was then compared with the reported antitumor activity. Statistical significance of proposed models was further investigated using Chi-square test and intercorrelation analysis. Accuracy of prediction using proposed models was found to vary from 80% to ~84%.
Keywords
Topochemical Indices; Wiener’s Topochemical Index; Molecular Connectivity Topochemical Index; Augmented Eccentric Connectivity Topochemical Index; Antitumor Activity; N-(phenylsulfonyl) benzamides.
Introduction
One important field of research in contemporary chemistry is the modeling and prediction of physico-chemical and biological properties of molecules. This kind of study is based on the paradigm that physico-chemical and biological properties are dependent on molecular structure [1]. Molecular structure can be represented by planar graph, G={V, E}, where the vector set V represents the atoms and the edge set E represents the bonds [2]. Invariants derived from graphs are properties, which have the same value for isomorphic graphs [3,4]. Spialter was the first to search for a graph invariant which could uniquely characterize the topology of molecular graphs [5]. One of the reason for the current upsurge of interest is the fact that such descriptors can be derived algorithmically i.e. can be computed from nay molecule real or hypothetical using computer software [6]. The topological description of a molecule contains information on the atom-atom connectivity in the molecule, and encodes the size, shape and branching features that determine the molecular properties. This graph description of molecules neglects information on bond lengths, bond angles and torsion angles [7]. The topostructural and topochemical descriptors are collectively referred to as topological descriptor. Topostructural descriptors encode information strictly on the adjacency and connectedness of atoms within a molecule, where as topochemical descriptors encode information related to both molecular topology and the chemical nature of atoms and bonds within a molecule [8]. A limited number of topostructural and topochemical indices have shown their successful applications in structure activity relationships. Some of the these topostructural indices include, Wiener’s index [9,10], Hosoya’s index [11,12], Randic’s molecular connectivity index [13,14], Zagreb group parameters [15,16], Balaban’s index [17,18], the higher-order connectivity indices, nc, for the paths of length n defined by Kier and Hall [19], eccentric connectivity index [20-23], Superpendentic index [24], revised Wiener index [25] and connective eccentricity index [26]. Topochemical indices, which have been successfully employed in SARs include molecular connectivity topochemical index [27,28], eccentric adjacency topochemical index [29], eccentric connectivity topochemical index [30], Weiner’s topochemical index [31], superadjacency topochemical index [32] and Zagreb topochemical indices [33] etc.
Colorectal cancer (CRC) is a common and lethal disease. Recently, important developments in the treatment (both surgical and chemotherapeutic) of colorectal cancer have occurred [34]. Despite decades of advances in the treatment and prevention of CRC, it remains the second most common cause of cancer death. However, the optimal method for early detection remains unknown and patient compliance with screening recommendations remains poor. This has led to the development of complementary strategies, such as chemoprevention to reduce morbidity and mortality from CRC [35]. In the last two decades, major progresses have been made in the management of patients with advanced colorectal cancer. The modulation of 5-fluorouracil by folinic acid, followed by the introduction of irinotecan and oxaliplatin have significantly improved the outcome of patients [36]. Bevacizumab (Avastin), the first approved therapy designed to inhibit tumor angiogenesis, has significant clinical benefits in the management of CRC. When bevacizumab is added to 5-fluorouracil/leucovorin/irinotecan as first-line therapy for metastatic CRC, significant overall and progression-free survival benefits has been obtained. Phase III trials are studying the benefit of combining bevacizumab with oxaliplatin based regimens [37]. First-, second-, and third-line therapies for the treatment of metastatic colorectal cancer may influence choices for subsequent therapy. First-line treatment for metastatic colorectal cancer has been proven to prolong survival, control disease progression, and improve quality of life, without excessive toxicity. Second-line targeted therapy has been well tolerated and active in several trials, however, second-line therapies are still in question because of residual toxicities and triplet therapy is also emerging. Future developments will most likely occur in the areas of pharmacogenetics and pharmacogenomics to produce individualized therapies for patients [38].
In the present study, the relationship of Wiener’s topochemical index- a distance-based topochemical descriptor, molecular connectivity topochemical index- an adjacency-based topochemical descriptor and augmented eccentric connectivity topochemical index - an adjacency-cum-distance based topochemical descriptor with antitumor activity of N-(phenylsulfonyl) benzamides has been investigated.
Methodology
Calculation of topochemical indices
Wiener’s topochemical index (Wc): It is a improved form of oldest and most widely used distance based topological index – Wiener’s index [9-10] and this modified index takes into consideration the presence as well as relative position of heteroatom(s) in a molecular structure. Wiener’s topochemical index is defined as the sum of the chemical distances between all pairs of vertices in hydrogen suppressed molecular graph [31], i.e.
|
|
(1) |
where ![]() is the chemical length of the path that
contains the least number of edges between vertex i and j in the
graph G, n is the number of vertices (maximum possible number of i
and j).
is the chemical length of the path that
contains the least number of edges between vertex i and j in the
graph G, n is the number of vertices (maximum possible number of i
and j).
Molecular connectivity topochemical index (cA): Molecular connectivity topochemical index is a modified form of the most widely used adjacency based topological index - molecular connectivity index [13,14] and it takes into consideration the presence as well as relative position of heteroatom(s) in a molecular structure. The molecular connectivity topochemical index [27,28] is defined as the summation of the modified bond values of adjacent vertices for all the edges in the hydrogen suppressed molecular graph as per the following equation:
|
|
(2) |
where, n is the number of vertices, Vci and Vcj are the modified degrees of adjacent vertices i and j forming the edge {i, j} in a graph G. The modified degree of a vertex can be obtained from the adjacency matrix by substituting row element corresponding to heteroatom, with relative atomic weight with respect to carbon atom.
Augmented eccentric connectivity topochemical index (Acxc): It is the topochemical version of the adjacency-cum-distance based augmented eccentric connectivity index [39] and is defined as the summation of the quotients of the product of adjacent vertex chemical degrees and chemical eccentricity of the concerned vertex, for all vertices in the hydrogen suppressed molecular graph. It is expressed as
|
|
(3) |
where, Mic is the product of chemical degrees of all vertices (vj), adjacent to vertex i, Eic is the chemical eccentricity, and n is the number of vertices in graph G. Augmented eccentric connectivity topochemical index is modification of the eccentric connectivity index, with augmented discriminating power and sensitivity towards the presence and relative position of heteroatom(s). Augmented eccentric connectivity topochemical index is calculated from the chemical distance matrix (Dc) and additive chemical adjacency matrix (Aac) obtained by modifying chemical adjacency matrix (Ac) [40].
Model design and analysis
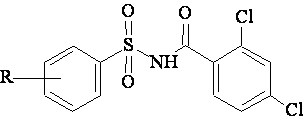
A data set [41] comprising 62 analogues of N-(phenylsulfonyl)benzamides was selected for the present investigation. The basic structure for these analogues is depicted in figure 1 and various substituents are enlisted in table 1.
|
A
B |
Figure 1. Basic structure of N-(phenylsulfonyl)benzamides
Table 1. Relationship of Wiener’s topochemical index, molecular connectivity topochemical index and augmented eccentric connectivity topochemical index with antitumor activity
|
Compd No. |
R |
Wc |
cA |
Acxc |
Antitumor activity Predicted Reported |
|||
|
Wc |
cA |
Acxc |
|
|||||
|
A1 |
2, 4 – diCl |
1255.808 |
7.885 |
29.681 |
± |
– |
± |
+ |
|
A2 |
H |
952.511 |
7.683 |
31.190 |
– |
– |
± |
– |
|
A3 |
2 – Cl |
1088.181 |
7.800 |
32.724 |
– |
– |
– |
– |
|
A4 |
3 – Cl |
1101.180 |
7.767 |
28.906 |
– |
– |
– |
– |
|
A5 |
4 – Cl |
1114.180 |
7.767 |
26.502 |
– |
– |
– |
– |
|
A6 |
2 – CH3 |
1069.579 |
8.093 |
32.146 |
– |
– |
± |
– |
|
A7 |
3 – Br |
1136.416 |
7.503 |
24.118 |
– |
+ |
– |
– |
|
A8 |
2 – NO2 |
1438.976 |
8.738 |
28.021 |
± |
± |
– |
– |
|
A9 |
4 – N(CH3)2 |
1431.983 |
8.871 |
28.495 |
± |
± |
– |
– |
|
A10 |
3, 4 – diCl |
1267.808 |
7.918 |
27.931 |
± |
– |
– |
– |
|
A11 |
2, 5 – diCl |
1243.808 |
7.885 |
31.450 |
± |
– |
+ |
– |
|
A12 |
3, 5 – diCl |
1255.808 |
7.851 |
30.926 |
± |
– |
± |
– |
|
A13 |
2 – Cl, 4 – Br |
1292.898 |
7.621 |
26.289 |
+ |
+ |
– |
+ |
|
A14 |
2 – Br, 4 – Cl |
1292.898 |
7.635 |
30.673 |
+ |
+ |
± |
+ |
|
A15 |
2, 4 – diBr |
1329.988 |
7.371 |
31.091 |
+ |
+ |
± |
+ |
|
A16 |
2 – F, 4 – Br |
1279.148 |
7.801 |
24.509 |
+ |
– |
– |
– |
|
A17 |
2 – CH3, 4 – Cl |
1236.228 |
8.178 |
27.673 |
± |
++ |
– |
+ |
|
A18 |
2 – CH3, 4 – Br |
1273.318 |
7.914 |
23.754 |
+ |
– |
– |
+ |
|
A19 |
2 – Cl, 4 – NO2 |
1592.333 |
8.856 |
30.816 |
± |
± |
± |
+ |
|
A20 |
2 – C2H5, 4 – Cl |
1379.275 |
8.716 |
28.277 |
+ |
± |
– |
+ |
|
A21 |
2 – Propyl, 4 – Cl |
1544.323 |
9.216 |
28.621 |
± |
– |
– |
– |
|
A22 |
2, 4 – diCH3 |
1216.648 |
8.487 |
31.561 |
– |
± |
+ |
– |
|
A23 |
2 – OCH3, 4 – Cl |
1389.432 |
8.562 |
28.696 |
+ |
± |
– |
– |
|
A24 |
2 – NH2, 4 – Cl |
1237.898 |
8.142 |
27.844 |
± |
– |
– |
– |
|
A25 |
2, 4 –bis(CF3) |
2258.532 |
10.317 |
33.295 |
– |
– |
– |
– |
|
A26 |
2 – NO2, 4 – Cl |
1540.333 |
8.841 |
29.668 |
± |
± |
– |
– |
|
A27 |
2 – NO2, 4 – CF3 |
2089.114 |
10.065 |
31.873 |
– |
– |
± |
– |
|
A28 |
2 – NO2, 4 – NO2 |
1899.944 |
9.812 |
31.035 |
– |
– |
± |
– |
|
A29 |
2 – Cl, 4 – CN |
1407.029 |
8.689 |
30.672 |
± |
± |
± |
– |
|
A30 |
2 – Cl, 4 – SO2CH3 |
1881.221 |
8.520 |
34.761 |
– |
± |
– |
– |
|
A31 |
2 – Cl, 4 – OCH3 |
1415.432 |
8.575 |
30.502 |
± |
± |
± |
– |
|
A32 |
2 – Cl, 4 – OH |
1239.558 |
8.123 |
32.516 |
± |
– |
– |
– |
|
A33 |
2 – Cl, 4 – NH2 |
1237.898 |
8.157 |
32.892 |
± |
– |
– |
– |
|
A34 |
2, 4 – diOCH3 |
1554.097 |
9.252 |
29.709 |
± |
– |
± |
– |
|
B1 |
H |
1077.513 |
7.800 |
31.550 |
– |
– |
+ |
+ |
|
B2 |
4 – CH3 |
1236.228 |
8.194 |
30.957 |
± |
++ |
± |
+ |
|
B3 |
4 – Br |
1292.898 |
7.621 |
26.512 |
+ |
+ |
– |
+ |
|
B4 |
3 – Br |
1278.898 |
7.621 |
29.728 |
+ |
+ |
± |
+ |
|
B5 |
4 – OCH3 |
1426.100 |
8.575 |
30.139 |
± |
± |
± |
+ |
|
B6 |
4 – tert-butyl |
1781.375 |
9.406 |
31.424 |
– |
– |
+ |
+ |
|
B7 |
3 – Cl, 4 – CH3 |
1404.503 |
8.312 |
31.756 |
+ |
++ |
+ |
+ |
|
B8 |
3 – Cl, 4 – F |
1410.624 |
8.206 |
31.962 |
± |
++ |
± |
+ |
|
B9 |
4 – F |
1242.058 |
8.076 |
30.552 |
± |
– |
± |
+ |
|
B10 |
3 – Cl |
1241.808 |
7.885 |
31.276 |
± |
– |
+ |
+ |
|
B11 |
3,4 – diCl |
1425.062 |
8.036 |
31.495 |
± |
– |
+ |
+ |
|
B12 |
4 – SCH3 |
1466.787 |
8.215 |
29.867 |
± |
++ |
± |
+ |
|
B13 |
4 – acetyl |
1601.322 |
9.029 |
30.592 |
± |
± |
± |
+ |
|
B14 |
3 – CH3 |
1222.228 |
8.194 |
32.253 |
± |
++ |
± |
+ |
|
B15 |
3,4 – diBr |
1502.951 |
7.576 |
30.432 |
± |
+ |
± |
+ |
|
B16 |
3 – NO2 |
1571.669 |
8.856 |
32.067 |
± |
± |
± |
+ |
|
B17 |
3 – OCH3 |
1398.100 |
8.575 |
31.534 |
+ |
± |
+ |
+ |
|
B18 |
4 – N(CH3)2 |
1606.343 |
8.988 |
30.754 |
± |
± |
± |
+ |
|
B19 |
3 – C6H6 |
2152.806 |
10.767 |
31.825 |
– |
– |
+ |
+ |
|
B20 |
4 – CO2CH3 |
1817.359 |
9.423 |
30.203 |
– |
± |
– |
|
|
B21 |
4 – NO2 |
1613.669 |
8.856 |
30.689 |
– |
± |
± |
– |
|
B22 |
4 – C6H6 |
2236.806 |
10.767 |
30.644 |
– |
– |
± |
– |
|
B23 |
3,4 – diOCH3 |
1764.685 |
9.375 |
31.894 |
– |
– |
± |
– |
|
B24 |
2 – Cl |
1227.808 |
7.948 |
33.731 |
± |
– |
– |
– |
|
B25 |
2 – Cl, 5 – NO2 |
1742.652 |
9.003 |
35.281 |
– |
± |
– |
– |
|
B26 |
2 – CH3, 5 – NO2 |
1720.135 |
9.281 |
33.250 |
– |
– |
– |
– |
|
B27 |
2 – Br, 4 – CH3 |
1430.447 |
8.104 |
35.234 |
± |
– |
– |
– |
|
B28 |
3,5 – diCl |
1412.062 |
7.969 |
33.681 |
± |
– |
– |
– |
+, Active analogues; ++, Very active analogues; –, Inactive analogues;
±, Transitional analogues where biological activity could not be specifically assigned
The values of the Wiener’s topochemical index were computed for each analogue using an in-house computer program. For the selection and evaluation of range specific features, exclusive activity ranges were discovered from the frequency distribution of response level and subsequently identifying the active range by analyzing the resultant data by maximization of the moving average with respect to the active compounds (<35% = inactive, 35-65% = transitional, >65% = active) [42]. Subsequently, each analogue was assigned a biological activity that was then compared with the reported [41] antitumor activity. The antitumor activity was reported quantitatively as IC50 values at different concentrations. The analogues possessing IC50values of <1.0 mM were considered to be active and analogues possessing IC50values of >1.0 mM were considered to be inactive for the purpose of present study. The percentage degree of prediction of a particular range and overall degree of prediction of each model was calculated.
Aforementioned procedure was similarly followed for molecular connectivity topochemical index, cA and augmented eccentric connectivity topochemical index, Acxc.
The statistical significance of association between Wiener’s topochemical index, molecular connectivity topochemical index and augmented eccentric connectivity topochemical index and distribution of correctly predicted derivatives in active range, very active range, transitional range and inactive range was determined using Chi-square test. A value of p<0.05 was considered to be statistically significant. Further, intercorrelation between Wiener’s topochemical index, molecular connectivity topochemical index and augmented eccentric connectivity topochemical index was investigated using the index values of 62 analogues of N-(phenylsulfonyl)benzamides. The degree of correlation was appraised by the correlation coefficient r. Pairs of indices with r>0.97 are considerably highly intercorrelated, those with 0.90<r<0.97 are appreciably correlated, those with 0.50<r<0.89 are weakly correlated and finally the pairs of indices with low r values (<0.50) are not intercorrelated [43]. The results are summarized in Table 1, Table 2, Table 3, Table 4 and Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6.
Table 2. Proposed models for antitumor activity
|
Model Index |
Nature of range in proposed model |
Index Value |
Number of analogues in the range |
Number of analogues predicted correctly |
Percent accuracy |
Average IC50 (mM) |
|
Wc |
Lower Inactive Lower Transitional Active Upper Transitional Upper Inactive |
<1222.228 1222.228 – <1273.318 1273.318 – 1404.503 >1404.503 – <1613.669 >1613.669 |
08 13 11 18 12 |
07 N.A.* 09 N.A. 10 |
87.5 N.A. 81.82 N.A. 83.33 |
11.191(12.714) ** N.A. 0.935 (0.410) N.A. 7.543 (8.920) |
|
cA |
Active Lower Inactive Very Active Transitional Upper Inactive |
7.371 – 7.635 >7.635 – <8.178 8.178 – 8.312 >8.312 – <9.216 >9.216 |
07 21 06 17 11 |
06 15 06 N.A. 09 |
85.71 71.43 100.00 N.A. 81.82 |
2.441(0.348) 8.763 (12.093) 0.427 N.A. 6.411(7.689) |
|
Acxc |
Lower Inactive Lower Transitional Active Upper Transitional Upper Inactive |
<29.681 29.681 – <31.276 31.276 – 31.825 >31.825 – <32.516 >32.516 |
16 21 09 06 10 |
11 N.A. 07 N.A. 10 |
68.75 N.A. 77.78 N.A. 100.00 |
5.449 (7.745) N.A. 2.191 (0.574) N.A. 13.680 |
|
*Not applicable **Values in the bracket indicate average IC50 values of correctly predicted analogues in the particular range. |
||||||
Table 3. Statistical association between Wiener’s topochemical index (Wc), molecular connectivity topochemical index (cA) and augmented eccentric connectivity topochemical index (Acxc) and activity ranges
|
Number of derivatives |
Wc |
cA |
Acxc |
|
Active |
9 |
6 |
7 |
|
Very Active |
0 |
6 |
0 |
|
Inactive |
17 |
24 |
21 |
|
Transitional |
31 |
17 |
27 |
|
Wrongly predicted |
5 |
9 |
7 |
|
Total |
62 |
62 |
62 |
Table 4. Intercorrelation matrix between Wiener’s topochemical index (Wc), molecular connectivity topochemical index (cA) and augmented eccentric connectivity topochemical index (Acxc)
|
|
Wc |
cA |
Acxc |
|
Wc |
1 |
0.894 |
0.309 |
|
cA |
|
1 |
0.264 |
|
Acxc |
|
|
1 |
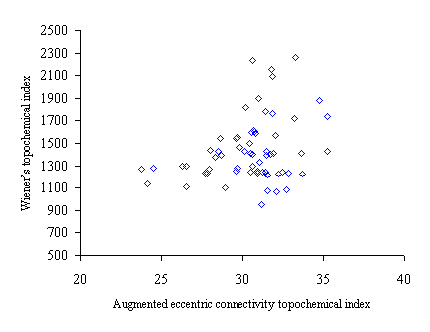
Figure 2. Intercorrelation between augmented eccentric connectivity topochemical index (Acxc) and Wiener’s topochemical index (Wc)
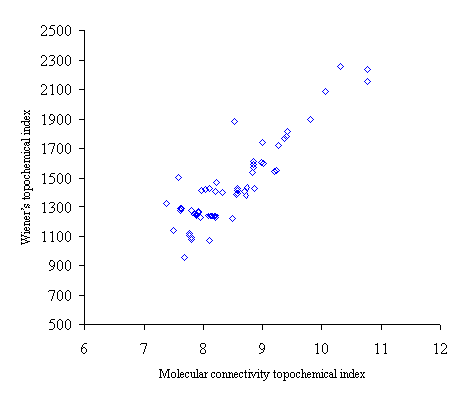
Figure 3. Intercorrelation between molecular connectivity topochemical index (cA) and Wiener’s topochemical index (Wc)
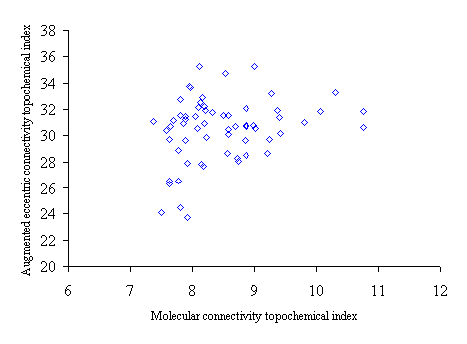
Figure 4. Intercorrelation between molecular connectivity topochemical index (cA) and augmented eccentric connectivity topochemical index (Acxc)
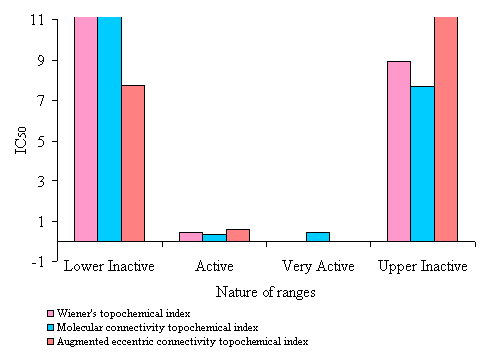
Figure 5. Average IC50 (mM) value of N-(phenylsulfonyl)benzamides of correctly predicted analogues in various ranges of topochemical models.
Results and Discussion
Relationship of Wiener’s topochemical index - a distance-based topochemical descriptor, molecular connectivity topochemical index - an adjacency-based topochemical descriptor and augmented eccentric connectivity topochemical index - an adjacency-cum-distance based topochemical descriptor with antitumor activity of N-(phenylsulfonyl)benzamides was studied and suitable models were developed for prediction of antitumor activity. Though all the analogues in the datasets possess varying degree of biological activity but only those analogues having IC50 values of <1.0 nM were considered to be active for the purpose of present study. The methodology used in the present studies aims at the development of suitable models for providing lead molecules through exploitation of the active ranges in the proposed models based on topochemical indices. Proposed models are unique and differ widely from conventional QSAR models. Both system of modeling have relative advantages and limitations. In the instant modeling, the system adopted has distinct advantage of identification of narrow active range(s), which may be erroneously skipped during regression analysis in conventional QSAR modeling. Since the ultimate goal of modeling is to provide lead structures, therefore, these active ranges can play vital role in providing lead structures [44].
Retrofit analysis of the data in table 1 and 2 reveals the following information with regard to models based upon Wiener’s topochemical index:
· A total of 31 out of 62 compounds were classified correctly in both the active and inactive ranges using the model based upon Wiener’s topochemical index. The overall accuracy of prediction was found to be ~84% with regard to antitumor activity.
· The active range had Wiener’s topochemical index values of 1273.318 to 1404.503. 82% of the analogues in the active range exhibited antitumor activity. The average IC50 value of active range was found to be only 0.935 mM. This clearly indicates high potency of the active range.
· Two inactive ranges - a lower inactive range with index values of <1222.228 and an upper inactive range with index values of >1613.669 were observed. Activity of 17 out of 20 compounds in these inactive ranges was predicted correctly.
· Two transitional ranges ideally bracketed the active range and indicate gradual transition from active to inactive range and vice versa. A lower transitional range with index values of 1222.228 to <1273.318 and an upper transitional range with index values of >1404.503 to <1613.669 was observed.
· The ratio of average IC50 values of active range and lower inactive range was found to be 1:12 (1:31 for correctly predicted analogues) and ratio of average IC50 values of active range and upper inactive range was found to be 1:8 (1:22 for correctly predicted analogues).
Retrofit analysis of the data in tables 1 and 2 reveals the following information with regard to model based upon molecular connectivity topochemical index:
· A total of 45 out of 62 compounds were classified correctly in both the active and inactive ranges using model based upon molecular connectivity topochemical index. The overall accuracy of prediction was found to be 80% with regard to antitumor activity.
· An active range with index values of 7.371 to 7.635 was observed. 92 % of the analogues in the active range exhibited antitumor activity. The average IC50value of active range was found to be 2.44 mM, indicating high potency of the active range.
· A very active range with index values of 8.178 to 8.312 was observed. 100 % of the analogues in the active range exhibited antitumor activity. The average IC50value of very active range was found to be 0.427 mM. This clearly indicates high potency of the very active range.
· Two inactive ranges - a lower inactive range with index values of >7.635 to < 8.178 and an upper inactive range with index values of >9.216 were observed. Activity of 15 out of 18 analogues in these inactive ranges was predicted correctly.
· A transitional range with index values of >8.312 to <9.216 was observed. The transitional range indicates gradual transition from active to inactive range and vice versa.
· The ratio of average IC50 values of active range and lower inactive range was found to be 1:4 (1:35 for correctly predicted analogues) and ratio of average IC50 values of active range and upper inactive range was found to be 1:3 (1:22 for correctly predicted analogues).
· The ratio of average IC50 values of very active range and lower inactive range was found to be 1:21 (1:28 for correctly predicted analogues) and ratio of average IC50 values of very active range and upper inactive range was found to be 1:15 (1:18 for correctly predicted analogues).
Retrofit analysis of the data in tables 1 and 2 reveals the following information with regard to augmented eccentric connectivity topochemical index:
· A total of 35 out of 62 compounds were classified correctly in both the active and inactive ranges using the model based upon augmented eccentric connectivity topochemical index. The overall accuracy of prediction was found to be 80% with regard to antitumor activity.
· The active range had augmented eccentric connectivity topochemical index values of 31.276 to 31.825. 78% of the analogues in the active range exhibited antitumor activity. The average IC50 value of active range was found to be only 2.191 mM. This clearly indicates high potency of the active range.
· Two inactive ranges - a lower inactive range with index values of <29.681 and an upper inactive range with index values of >32.516 were observed. Activity of 21 out of 26 compounds in these inactive ranges was predicted correctly.
· Two transitional ranges ideally bracketed the active range and indicate gradual transition from active to inactive range and vice versa. A lower transitional range with index values of 29.681 to <31.276 and an upper transitional range with index values of >31.825 to <32.516 was observed.
· The ratio of average IC50 values of active range and lower inactive range was found to be 1:3 (1:14 for correctly predicted analogues) and ratio of average IC50 values of active range and upper inactive range was found to be 1:6 (1:24 for correctly predicted analogues).
The Wiener’s topochemical index, molecular connectivity topochemical index and augmented eccentric connectivity topochemical index (table 3) were found to be statistically different for distribution of the derivatives into various activity ranges. There is relationship between these graph invariants (Wiener’s topochemical index, molecular connectivity topochemical index and augmented eccentric connectivity topochemical index) and distribution of derivatives in activity ranges because p<0.05.
Intercorrelation analysis (table 4) revealed that Wiener’s topochemical index is weakly correlated with the molecular connectivity topochemical index. The augmented eccentric connectivity topochemical index is not correlated with Wiener’s topochemical index and molecular connectivity topochemical index as well.
Conclusion
Investigations reveal significant correlations of all the three-topochemical indices with antitumor activity of N-(phenylsulfonyl)benzamides. The overall accuracy of prediction varied from minimum of 80% for models based on augmented eccentric connectivity topochemical and molecular connectivity topochemical index to a maximum of ~84% in case of Wiener’s topochemical index. High predictability of the proposed models based upon the topochemical indices offer a vast potential for providing lead structures for the development of potent agents with regard to antitumor activity.
References
1. Duart M. J., Anton-Fos G. M., De Julian-Ortiz J. V., Gozalbes R., Galvez J., Garcia-Domenech R., Use of molecular topology for the prediction of physico-chemical, pharmacokinetics and toxicological properties of a group of antihistaminic drugs, Int. J. Pharm., 2002, 246, p. 111-119.
2. Harary F., Graph Theory, Addison-Wesley Publishing Company, Reading, MA, 1969.
3. Trinajstic N., Chemical Graph Theory, 2nd Ed., CRC Press, Boca Raton, FL, 1992.
4. Basak S. C., Bertelsen S., Grunwald G. D., Use of graph theoretic parameters in risk assessment of chemicals, Toxicol. Lett., 1995, 79, p. 239-250.
5. Basak S. C., Bertelsen S., Grunwald G. D., Application of graph theoretical parameters in quantifying molecular similarity and structure-activity relationships, J. Chem. Inf. Comput. Sci., 1994, 34, p. 270-276.
6. Basak S. C., Gute B. D., Grunwald G. D., Use of topostructural, topochemical, and geometric parameters in the prediction of vapor pressure: A hierarchical QSAR approach, J. Chem. Inf. Comput. Sci., 1997, 37, p. 651-655.
7. Ivanciuc O., Taraviras S. L., Cabrol-Bass D., Quasi-orthogonal basis sets of molecular graph descriptors as a chemical diversity measure, J. Chem. Inf. Comput. Sci., 2000, 40, p. 126-134.
8. Basak S. C., Mills D., Hawkins D. M., EL-Masri H. A., Prediction of tissue-air partition coefficients: A comparison of structure-based and property-based methods, SAR and QSAR in Environ. Res., 2002, 13, p. 649-665.
9. Wiener H., Correlation of heat of isomerization and difference in heat of vaporization of isomers among paraffin hydrocarbons, J. Am. Chem. Soc., 1947, 69, p. 2636-2638.
10. Wiener H., Influence of interatomic forces on paraffin properties, J. Chem. Phys., 1947, 15, p. 766-766.
11. Hosoya H., Topological index; newly proposed quantity characterizing the topological nature of structure of isomers of saturated hydrocarbons, Bull. Chem. Soc. Jpn., 1971, 44, p. 2332-2337.
12. Hosoya H., Topological index as strong sorting device for coding chemical structure, J. Chem. Doc., 1972, 12, p. 181-183.
13. Randic M., On characterization of molecular branching, J. Am. Chem. Soc., 1975, 97, p. 6609-6615.
14. Randic M., The Connectivity index 25 years after, J. Mol. Graph. Mod., 2001, 20, p. 19-35.
15. Gutman I., Ruscic B., Trinajstic N., Wicox C. F., Graph theory and molecular orbitals. XII. acyclic polyenes, J. Chem. Phys., 1975, 62, p. 3399-3405.
16. Gutman I., Randic M., Algebraic characterization of skeletal branching, Chem. Phys. Lett., 1977, 47, p. 15-19.
17. Balaban A. T., Chiriac A., Motoc I., Simon Z., Steric fit in QSAR, Lect. Notes Chem., 1980, 15, p. 22-27.
18. Balaban A. T., Applications of graph theory in chemistry, J. Chem. Inf. Comput. Sci., 1985, 25, p. 334-343.
19. Kier L. B., Hall L. H., Molecular Connectivity in Structure-Activity Analysis, Research Studies Press, Letchworth, UK, 1986.
20. Sharma V., Goswami R., Madan A. K., Eccentric connectivity index: a novel highly discriminating topological descriptor for structure property and structure activity studies, J. Chem. Inf. Comput. Sci., 1997, 37, p. 273-282.
21. Gupta S., Singh M., Madan A. K., Application of graph theory: relationship of eccentric connectivity index and Wiener’s index with anti-inflammatory activity, J. Math. Anal. Applic., 2002, 266, p. 259-268.
22. Kumar V., Madan A. K., Topological Models for the Prediction of Cyclin-Dependent Kinase 2 Inhibitory Activity of Aminothiazoles, MATCH Commun. Math. Comput. Chem., 2004, 51, p. 59 -78.
23. Lather V., Madan A. K., Predicting Acyl-Coenzyme A: Cholesterol O-Acyltransferase Inhibitory Activity: Computational Approach using Topological Descriptors, Drug Design and Discovery, 2003, 18, p. 117-122.
24. Gupta S., Singh M., Madan A. K., Superpendentic index: a novel topological descriptor for prediction of biological activity, J. Chem. Inf. Comput. Sci., 1999, 39, p. 272-277.
25. Randic M., On generalization of Wiener index for cyclic structures, Acta Chim. Slov., 2002, 49, p. 483-496
26. Gupta S., Singh M., Madan A.K., Connective eccentricity index: a novel topological descriptor for predicting biological activity, J. Mol. Graph. Model., 2000, 18, p. 18-25.
27. Goel A., Madan A. K., Structure-activity study on anti-inflammatory pyrazole carboxylic acid hydrazide analogs using molecular connectivity indices, J. Chem. Inf. Comput. Sci., 1995, 35, p. 510-514.
28. Dureja H., Madan A. K., Topochemical models for prediction of cyclin-dependent kinase 2 inhibitory activity of indole-2-ones, J. Mol. Mod., 2005, 11, p. 525-531
29. Gupta S., Singh M., Madan A. K., Novel topochemical descriptors for predicting anti-HIV activit,. Indian J. Chem., 2003, 42A, p. 1414-1425.
30. Kumar V., Sardana S., Madan A. K., Predicting anti-HIV activity of 2,3-diaryl-1,3-thiazolidin-4-ones: computational approach using reformed eccentric connectivity index, J. Mol. Mod., 2004, 10, p. 399-407.
31. Bajaj S., Sambi S. S., Madan A. K., Predicting anti-HIV activity of phenethylthiazolethiourea (PETT) analogs: computational approach using Wiener’s topochemical index, J. Mol. Struct. (THEOCHEM), 2004, 684, p.197-203.
32. Bajaj S., Sambi S. S., Madan A. K., Prediction of carbonic anhydrase activation by tri-/tetrasubstituted-pyridinium-azole compounds: a computational approach using novel topochemical descriptor, QSAR & Comb. Sci., 2004, 23, p. 506-514.
33. Bajaj S., Sambi S. S., Madan A. K., Prediction of anti-inflammatory activity of N-arylanthranilic acids: computational approach using refined Zagreb indices, Croat. Chem. Acta, 2005, 78, p. 165-174.
34. Dekker E., Gulik T., Colorectal cancer: what the clinician wants to know, Cancer Imaging, 2005, 5, p. S127-S132.
35. Raju R., Cruz-Correa M., Chemoprevention of colorectal cancer, Dis. Colon Rectum, 2006, 49, p. 113-125.
36. Sultan-Amar V., Fabre-Guillevin E., Piedbois P., Progresses in the medical treatment of advanced colorectal cancer, Rocz. Akad. Med. Bialymst., 2005, 50, p. 97-100.
37. Diaz-Rubio E., Schmoll H., The future development of bevacizumab in colorectal cancer, J. Oncol., 2005, 69, p. 34-45.
38. Rougier P., Lepere C., Metastatic colorectal cancer: first- and second-line treatment in 2005, Semin. Oncol., 2005, 32, p. 15-20.
39. Bajaj S., Sambi S. S., Gupta S., Madan A. K., Model for prediction of Anti-HIV activity of 2-pyridinone derivatives using novel topological descriptor, QSAR & Comb. Sci., 2006, 25, p. 813-823.
40. Bajaj S., Study on topochemical descriptors for the prediction of physicochemical and biological properties of molecules, Ph.D. Thesis, Guru Gobind Singh Indraprastha University, India, 2005.
41. Lobb K. L., Hipskind P. A., Aikins J. A., Alvarez E., Cheung Y.-Y., Considine E. L., Dios A. D., Durst G. L., Ferritto R., Grossman C. S., Giera D. D., Hollister B. A., Huang Z., Iversen P. W., Law K. L., Li T., Lin H.-O., Lopez B., Lopez J. E., Cabrejas L. M. M., McCann D. J., Molero V., Reilly J. E., Richett M. E., Shih C., Teicher B., Wikel J. H., White W. T., Mader M. M., Acyl sulfonamide anti-proliferatives: benzene substituents structure-activity relationships for a novel class of antitumor agents, J. Med. Chem., 2004, 47, p. 5367-5380.
42. Gupta S., Singh M., Madan A. K., Predicting anti-HIV activity: computational approach using novel topological descriptor, J. Comput. Aid. Mol. Des., 2001, 15, p. 671-678.
43. Nikolic S., Kovacevic G., Milicevic A., Trinajstic N., The Zegrab indices 30 years after, Croat. Chem. Acta, 2003, 76, p. 113-124.
44. Dureja H., Madan A. K., Models for the prediction of h5-HT2A receptor antagonistic activity of arylindoles: computational approach using topochemical descriptors, J. Mol. Graph. Mod., 25, 2006, p. 373-379.