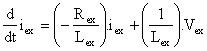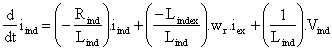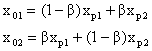Intelligent Controller Design for DC Motor Speed Control based on Fuzzy Logic-Genetic Algorithms Optimization
Boumediene ALLAOUA*, Abdellah LAOUFI, Brahim GASBAOUI, Abdelfatah NASRI and Abdessalam ABDERRAHMANI
Departement of Electrical Engineering, Bechar University, B.P 417 BECHAR (08000) Algeria
E-mail(s): elec_allaoua2bf@yahoo.fr, laoufi_ab@yahoo.fr, brahim_gasb@yahoo.com, nasriab1978@yahoo.fr, abderrahmani@yahoo.fr
Abstract
In this paper, an intelligent controller of the DC (Direct current) Motor drive is designed using fuzzy logic-genetic algorithms optimization. First, a controller is designed according to fuzzy rules such that the systems are fundamentally robust. To obtain the globally optimal values, parameters of the fuzzy controller are improved by genetic algorithms optimization model. Computer MATLAB work space demonstrate that the fuzzy controller associated to the genetic algorithms approach became very strong, gives a very good results and possesses good robustness.
Keywords
Direct current motor drive; Nonlinear control; Fuzzy logic controller; Genetic algorithm; Intelligent fuzzy control using genetic algorithms.
Introduction
In spite of the development of power electronics resources, the direct current machine became more and more useful. Nowadays their uses isn’t limited in the car applications (electrics vehicle), in applications of weak power using battery system (motor of toy) or for the electric traction in the multi-machine systems too.
The speed of DC motor can be adjusted to a great extent as to provide controllability easy and high performance [1, 2]. The controllers of the speed that are conceived for goal to control the speed of DC motor to execute one variety of tasks, is of several conventional and numeric controller types, the controllers can be: PID Controller, Fuzzy Logic Controller; or the combination between them Fuzzy-Genetic Algorithm, Fuzzy-Neural Networks, Fuzzy-Ants Colony, Fuzzy-Swarm (Swarm).
Fuzzy theory was first proposed and investigated by Prof. Zadeh in 1965. The Mamdani fuzzy inference system was presented to control a steam engine and boiler combination by linguistic rules [3, 7]. Fuzzy logic is expressed by means of if-then rules with the human language. In the design of a fuzzy logic controller, the mathematical model is not necessary. Thus, the fuzzy logic controller owns good robustness. Fuzzy controller has been widely used in industry for its easy realization. However, the rules and the membership functions of a fuzzy logic controller are constructed by expert experience or knowledge database.
Much work has been done on the analysis of fuzzy control rules and membership function parameters [3]. In 1960, Prof. Holland introduced genetic algorithms [4, 5]. Genetic algorithms are applied to search the globally optimal solution of problems. The evolution process of genetic algorithms is based on the natural selection. Genetic algorithms employ chromosomes through three operations, reproduction, crossover, and mutations to generate offspring for next iterations. The advantages of genetic algorithms are derivative-free stochastic optimization, parallel-search procedure and applicable to both continuous and discrete problems.
Recently, there have been some researches in discussing the design of fuzzy controller with genetic algorithms. In [5, 6, 7], genetic algorithms are applied to adjust the ranges of membership functions. However, the expert experiences or knowledge are still required for the shapes of membership functions and fuzzy inference rules. In [8, 9, 10], genetic algorithms are applied to choose membership functions and fuzzy rules. However, the expert experiences or knowledge are still necessary for the ranges of membership functions. In this paper, a novel strategy is proposed to design the optimal fuzzy controller.
Genetic algorithms are applied to search the globally optimal parameters of fuzzy logic. The best ranges of membership functions; the best shapes of membership functions and the best fuzzy inference rules are dug out at the same time. Furthermore, the performances of three different fuzzy logic controllers are compared. Computer simulations demonstrate the optimal design is effectiveness.
Model of DC Motor
DC machines are characterized by their versatility. By means of various combinations of shunt-, series-, and separately-excited field windings they can be designed to display a wide variety of volt-ampere or speed-torque characteristics for both dynamic and steady-state operation. Because of the ease with which they can be controlled systems of DC machines have been frequently used in many applications requiring a wide range of motor speeds and a precise output motor control [11, 12].
In this paper, the separated excitation DC motor model is chosen according to his good electrical and mechanical performances more than other DC motor models. The DC motor is driven by applied voltage. Fig.1 show the equivalent circuit of DC motor with separate excitation. The Symbols, Designations and Units are publicized in Table 1.
The characteristic equations of the DC motor are represented as:
|
|
(1) |
|
|
(2) |
|
|
(3) |
Table 1. Symbols, Designations and Units.
|
Symbols |
Designations |
Units |
|
iexandiend |
Excitation current and Induced current. |
[A] |
|
wr |
Rotational speed of the DC Motor. |
[Rad/Sec] |
|
VexandVind |
Excitation voltage and Induced voltage |
[Volt] |
|
RexandRind |
Excitation Resistance and Induced Resistance. |
[W] |
|
Lex,Lindand Lindex |
Excitation Inductance Induced Inductance and Mutual Inductance. |
[mH] |
|
|
Moment of Inertia. |
[Kg.m2] |
|
|
Couple resisting. |
[N.m] |
|
|
Coefficient of Friction. |
[N.m.Sec/Rad] |
The equivalent circuit of DC motor with separate excitation illustrated in Fig. 1.
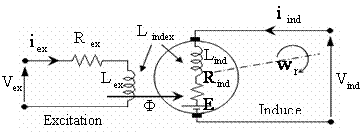
Figure 1. Equivalent circuit of DC motor with Separate Excitation.
From the state equations (1), (2), (3) previous, can construct the model with the environment MATLAB 7.4 (R2007a) in Simulink version 6.6. The model of the DC motor in Simulink is shown in Fig. 2. The various parameters of the DC motor are shown in Table 2.
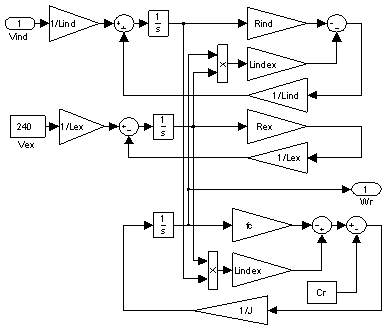
Figure 2. Model of the DC Motor in Simulink.
Table 2. Parameters of the DC Motor.
|
Vex=240[V] |
Lind=0.012[mH] |
|
Vind=240[V] |
Lindex=1.8[mH] |
|
Rex=240[W] |
|
|
Rind=0.6[W] |
|
|
Lex=120[mH] |
|
Zuzzy Logic Controller
Zuzzy logic is expressed by means of the human language [10]. Based on fuzzy logic, a fuzzy controller converts a linguistic control strategy into an automatic control strategy, and fuzzy rules are constructed by expert experience or knowledge database.
First, set the error 
and the error variation 
of the
angular velocity to be the input variables of the fuzzy logic controller. The
control voltage 
is the output variable of the fuzzy
logic controller.
The linguistic variables are defined as {NB, NS, Z, PS, PB}, where NB means negative big, NS means negative small, Z means zero, PS means positive small and PB means positive big. The membership functions of the fuzzy logic controller are shown in Fig. 3. The fuzzy rules are summarized in Table 3. The type of fuzzy inference engine is Mamdani. The fuzzy inference mechanism in this study follows as:
|
|
(4) |
where
is the membership function of , 
is the membership
function of 
, 
is the membership function of 
, j is an
index of every membership function of fuzzy set, m is the number of rules and
is the inference result. Fuzzy output 
can be calculated by the center of
gravity defuzzification as:
|
|
(5) |
where i is the output rule after inferring.
Table 3. Fuzzy inference rules.
|
|
|
|||||
|
NB |
NS |
Z |
PS |
PB |
||
|
|
NB |
NB |
NB |
NS |
NS |
Z |
|
NS |
NB |
NS |
NS |
Z |
PS |
|
|
Z |
NS |
NS |
Z |
PS |
PS |
|
|
PS |
NS |
Z |
PS |
PS |
PB |
|
|
PB |
Z |
PS |
PS |
PB |
PB |
|
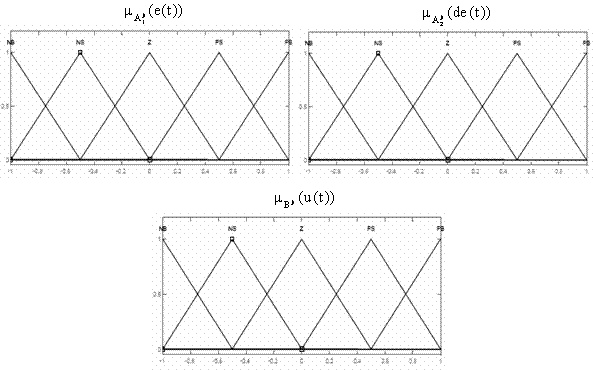
Figure 3. Membership function of fuzzy logic controller.
Genetic Algorithms
Genetic algorithms are developed by Prof. Holland [5, 6]. This methodology is a derivative free optimization technique based on the concept of natural selection and evolution processes. The genetic operations are reproduction, crossover and mutation.
The evolution procedure of GAs is shown in Fig. 4. Producing initial populations is the first step of GAs. The population is composed of the chromosomes that are binary bit string or real codes. The corresponding evaluation of a population is called the “fitness function”. It is the performance index of a population. The fitness value is bigger, and the performance is better. The fitness function is defined as follow:
|
|
(6) |
where “PI” is the fitness value, e is the speed error and “
” is a
constant.
After the fitness function is calculated, the fitness value and the number of the generation determine whether the evolution procedure is stopped or not. In the following, the new populations are generated through reproduction, crossover and mutation. The selection operation decides which parents take part in reproducing offspring for the next generation. The crossover operation is applied to generate new chromosomes. The equations of the new populations generated from crossover are:
|
|
(7) |
Where xp1 and xp2 are the old chromosomes, b is the random value from 0 to 1, x01 and x02 are the new chromosomes. Mutation is a method to find the global optimal values. It changes the chromosomes from a random value.
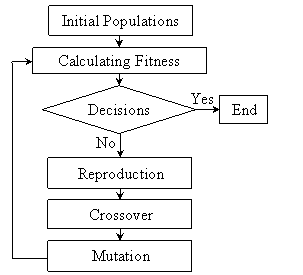
Figure 4. The evolution procedure of GAs.
Optimal Fuzzy Controller Design
To design the optimal fuzzy controller, the genetic algorithms are applied to search the globally optimal parameters of the fuzzy logic. The structure of the fuzzy logic controller with genetic algorithms is shown in Fig. 5.
In this paper, the chromosomes of the genetic algorithms include three parts: the range of the membership functions (Ke and Kde), the shape of the membership functions (e1~e5, de1~de5 and u1~u5) and the fuzzy inference rules (r1~r25). It makes the output voltage to be optimal such that the steady-state error of the response is zero. The genes in the chromosomes are defined as:
|
[Ke, Kde, e1, e2, e3, e4, e5, de1, de2, de3, de4, de5, u1, u2, u3, u4, u5, r1, r2, r3, r4, r5, r6, r7, r8, r9, r10, r11, r12, r13, r14, r15, r16, r17, r18, r19, r20, r21, r22, r23, r24, r25] |
(8) |
Fig. 6 shows the membership functions of the fuzzy logic controller with GAs. Table 4 lists the fuzzy inference rules with GAs. Table 5 lists the parameters of genetic algorithms used in this paper. The fuzzy inference rules (r1~r25) are replaced of 1 (NB), 2 (NS), 3 (Z), 4(PS) and 5 (PB).
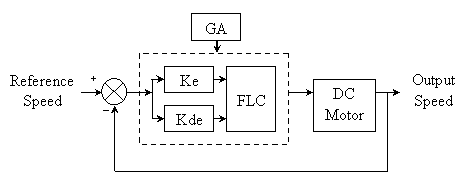
Figure 5. FLC with GAs structure.
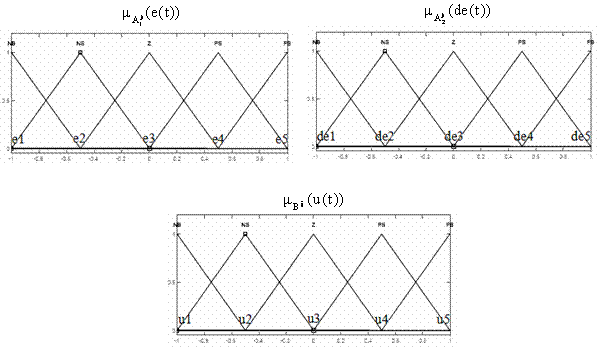
Figure 6. Membership functions of fuzzy logic controller with GAs.
Table 4. Fuzzy inference rules.
|
|
|
|||||
|
NB |
NS |
Z |
PS |
PB |
||
|
|
NB |
r1 |
r6 |
r11 |
r16 |
r21 |
|
NS |
r2 |
r7 |
r12 |
r17 |
r22 |
|
|
Z |
r3 |
r8 |
r13 |
r18 |
r23 |
|
|
PS |
r4 |
r9 |
r14 |
r19 |
r24 |
|
|
PB |
r5 |
r10 |
r15 |
r20 |
r25 |
|
Table 5. Parameters of GA.
|
Population |
42 |
|
Generation |
50 |
|
Crossover |
0.9 |
|
Mutation |
0.08 |
|
Min-offset |
200 |
|
Ke and Kde |
[0.001 0.005] |
|
e1, de1 and u1 |
[-1 -0.5] |
|
e2, de2 and u2 |
[-1 0] |
|
e3, de3 and u3 |
[-0.5 +0.5] |
|
e4, de4 and u4 |
[0 +1] |
|
e5, de5 and u5 |
[+0.5 +1] |
Computer Simulation
Three different fuzzy logic controllers are designed for the computer simulation. First, the fuzzy logic controller is designed based on the expert experience as described in section 3. Second, the fuzzy logic controller is designed based on the genetic algorithms to only find the optimal range of the membership functions (FLC1 with GAs). Last, the optimal fuzzy controller is designed based on the genetic algorithms to search the optimal range of the membership functions, the optimal shape of the membership functions and the optimal fuzzy inference rules (FLC2 with GAs).
After the evolution process, the optimal values of Ke and Kde in FLC1 with GAs are calculated as 0.005 and 0.005, respectively. The best chromosomes in FLC2 with GAs are pursued as:
|
[ 0.0047, 0.0039, -0.7860, -0.6640, 0.2778, 0.6323, 0.6693, -0.7963, -0.7275, 0.4050, 0.1561, 0.8070, -0.6799, -0.1561, -0.0661, 0.1085, 0.5899, 1, 1, 1, 2, 4, 5, 2, 3, 3, 5, 5, 3, 1, 1, 1, 4, 4, 4, 3, 3, 5, 1, 2, 3, 3] |
(9) |
The optimal membership functions are shown in Fig. 7. The optimal fuzzy inference rules are listed in Table 6.
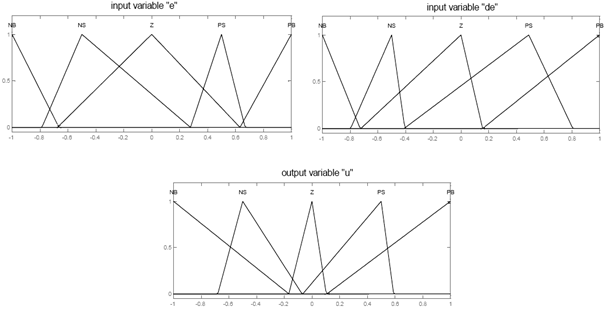
Figure 7. The optimal membership functions.
Table 6. The optimal fuzzy rules.
|
|
|
|||||
|
NB |
NS |
Z |
PS |
PB |
||
|
|
NB |
NB |
PB |
PB |
PS |
PB |
|
NS |
NB |
NS |
NB |
PS |
NB |
|
|
Z |
NB |
Z |
NB |
PS |
NS |
|
|
PS |
NS |
Z |
NB |
Z |
Z |
|
|
PB |
PS |
PB |
NB |
Z |
Z |
|
Let the command signal be a step for the speed of the DC motor at 127.93 Rad/Sec. The simulation results are obtained for 0.1 second range time.
The speed response of FLC (Fuzzy Logic Controller) without GAs is shown in Fig 8. The speed response of FLC1 with GAs is shown in Fig 9. The speed response of the optimal fuzzy controller is shown in Fig 10.
The performances of three different fuzzy logic controllers are listed in Table 7.
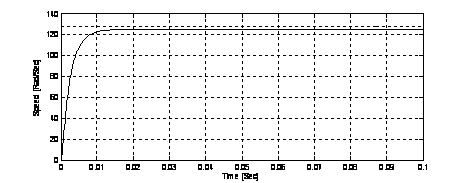
Figure 8. The speed response of FLC without GAs.
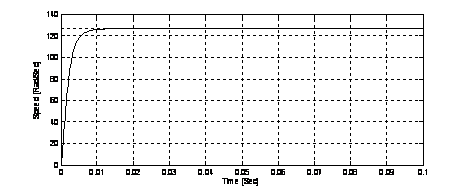
Figure 9. The speed response of FLC1 with GAs.
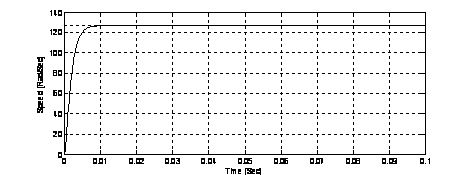
Figure 10. The speed response of FLC2 with GAs.
Table 7. Performances of three fuzzy logic controllers.
|
Results |
FLC without GAs |
FLC1 with GAs |
FLC2 with GAs |
|
Rising time [Sec] |
0.0207 |
0.0114 |
0.0088 |
|
Overtaking [%] |
0 |
0 |
0 |
|
Steady state error [%] |
0.45 |
0 |
0 |
According to our MATLAB model simulation, we illustrate that the steady state error equal zero in two cases: FLC1 with GAs and FLC2 with GAs (Figure 9 and 10); the overtaking value is zero in the three cases that means the FLC used is robust. The rising time of DC motor speed step is less important in FLC1 with GAs compared with FLC alone and it’s have the minimal value in The FLC2 with GAs.
In the present work, the intelligent controller based on Fuzzy Logic-Genetic Algorithms optimisation give a good agreement with the step reference speed. In the fuzzy logic DC motor control, the optimization of membership functions and rules became very necessary, it’s important shown in the minimal rising time of speed response, so the membership functions are adjusted in optimal values to give a steady state error speed value equal zero. The computer MATLAB simulation demonstrate that the fuzzy controller associated to the genetic algorithms approach became very strong, gives a very good results and possesses good robustness.
Conclusions
In this paper, the speed of a DC Motor drive is controlled by means of three different fuzzy controllers. The optimal fuzzy logic is designed using genetic algorithms. According to the results of the computer simulation, the FLC1 with GAs is better than the traditional FLC without GAs. The FLC2 with GAs is the best controller which presented satisfactory performances and possesses good robustness (no overshoot, minimal rise time, Steady state error = 0). The major drawback of the fuzzy controller is the insufficient analytical design technique (choice of the rules, the membership functions and the scaling factors). That we chose with the use of the genetic algorithm for the optimization of this controller in order to control DC motor speed. Finally, the proposed controller provides drive robustness improvement.
References
1. Hénao H., Capolino G.A., Méthodologie et application du diagnostic pour les systèmes électriques, Article invité dans Revue de l'Electricité et de l'Electronique (REE), n°6, pp.79-86. (Text in french), June 2002.
2. Raghavan S., Digital control for speed and position of a DC motor, MS Thesis, Texas A&M University, Kingsville, August 2005.
3. Yen J., Langari R., Fuzzy logic: Intelligence, Control, and Information, Prentice-Hall, 1999.
4. Swarup K.S., Yamashiro S., Unit commitment solution methodology using genetic algorithm, IEEE Trans: Power System, vol. 17, pp. 87–91, 2002.
5. Gen M., Cheng R., Genetic Algorithms and Engineering Design, John Wiley and Sons, INC, 1997.
6. Belarbi K., Titel F., Genetic Algorithm for the Design of a Class of Fuzzy Controllers An Alternative, IEEE Trans: On Fuzzy Systems, Vol. 8, No. 3 pp. 398-405, 2000.
7. Zhou Y. S., Lai L. Y., Optimal Design for Fuzzy Controllers by Genetic Algorithms, IEEE Trans: On Industry Application, Vol. 36, No. 1 pp. 93-97, 2000.
8. Hazzab A., Bousserhane I.K., Kamli M., Design of fuzzy sliding mode controller by genetic algorithms for induction machine speed control, International Journal of Emerging Electric Power System, Vol. 01, No. 02, 2004.
9. Lee M., Takagi H., Integrating design stages of fuzzy systems using genetic algorithms, Proc. 2nd IEEE Internat. Conf. on Fuzzy Systems, San Francisco, CA, pp. 612-617, 1993.
10. Foran J., Optimisation of a Fuzzy Logic Controller Using Genetic Algorithms, Doctorat, Texas University of America, USA, 2002.
11. Halila A., Étude des machines à courant continu, MS Thesis, University of LAVAL, (Text in French), May 2001.
12. Capolino G. A., Cirrincione G., Cirrincione M., Henao H., Grisel R., Digital signal processing for electrical machines, International Conference on Electrical Machines and Power Electronics, Kusadasi (Turkey), pp.211-219, 2001.