Application of SUMT Method to Combine Economic and Emission Dispatch

 

Lahouaria BENASLA, Abderrahim BELMADANI and Mustapha RAHLI

 

Department of Electrical Engineering,U.S.T.O, B.P 1505, Oran El M’naouar, Oran, Algeria.

Department of Computer Science U.S.T.O, B.P 1505, Oran El M’naouar, Oran, Algeria.

 

E-mail(s): jbenasla@yahoo.fr. belmadan@univ-usto.dz, rahlim@yahoo.fr.

 

Abstract

This paper presents a new approach for solving the combined economic and emission dispatch problem under some equality and inequality constraints. The equality constraints reflect a real power balance, and the inequality constraints reflect the limits of real generation. The voltage levels and security are assumed to be constant. The problem is solved by a Sequential Unconstrained Minimization Technique (SUMT) algorithm which was developed by Fiacco and McCormick. Combined economic emission dispatch problem is obtained by considering both the economy and emission objectives. This bi-objective problem is converted into a single objective function using a price penalty factor. In this paper SUMT method is tested on three generators system and its results are compared with the solutions obtained in [1]. The results are quite encouraging and useful in the economic emission environment.

Keywords

Economic Dispatch; Emission Dispatch; Combined Economic Emission Dispatch; Penalty Function Methods; SUMT Method.

 

Introduction

 

Economic dispatch is one of the most important optimization problems in power system operation and forms the basis of many application programs. The main objective of economic load dispatch of electric power generation is to schedule the committed generating unit outputs so as to meet the load demand at minimum operating cost while satisfying all unit and system constraints. One of those constraints which always took into account is the environmental constraint. That is minimization of pollution emission (NOx, CO2, SO2, small quantities of toxic metals, etc) in case of power plants. However, the rise of interests in environment problem in the recent years, it become necessary for power utilities to count this constraint as one of the main objectives, which should be solved together with the cost problem [2]. Thus, we are facing with a bi-objective optimization problem to deal with. This problem is converted into mono-objective optimisation problem by introducing price penalty factor.

In this paper, SUMT method [3, 4] is applied to solve combined economic and emission dispatch problem. A three generators system is considered to investigate the effectiveness of the proposed algorithm.

 

 

Problem formulation

 

Economic dispatch

Economic dispatch is the important component of power system optimization. It is defined as the minimization of the combination of the power generation, which minimizes the total cost while satisfying the power balance relation. The problem of economic dispatch can be formulated as minimization of the cost function subjected to the equality and inequality constraints [5].

Minimize the cost function

                                                                    (1)

Where  is the total fuel cost of the system, is the number of generators,, and are the cost coefficients of the i-th unit.

Emission dispatch

The emission function can be expressed as the sum of all types of emission considered, such as NOx, SO2, CO2, particles and thermal emissions, ect, with suitable pricing of weighting on each pollutant emitted [6].

In the present study, only one type of emission (NOx) is taken into account. The NOx emissions of the system are expressed as follows:

                                                                                            (2)

Where  is the total NOx emission of the system, , and are the emission coefficients of the i-th unit.

Constraints

Equality constraints

The total power generation must cover the total demand  and the transmission loss of the system. Hence,

                                                                                      (3)

 

Inequality Constraints

Generation power should be within the minimum output  and the maximum output.

                                                                                      (4)

 

Combined economic and emission dispatch

Aggregating equations (1) to (4), the power dispatch problem is expressed as a bi-objective optimization problem as follows

                                                                                        (5)

The bi-objective combined economic emission dispatch problem is converted into single optimization problem by introducing price penalty factor  as follows:

                                                                          (6)

Subject to the power constraints given by (3) and (4).

The price penalty factor  is the ratio between the maximum fuel cost and maximum emission of corresponding generator [1, 7]

                                                                                                 (7)

The steps to determine the price penalty factor for a particular load demand are:

1.      Find the ratio between maximum fuel cost and maximum emission of each generator.

2.      Arrange  (i=1,2…,ng) in ascending order.

3.      Add the maximum capacity of each unit (PGimax) one at a time, starting from the smallest Pfi until .

4.      In this stage, Pfi associated with the last unit in the process is the price penalty factor of the given load.

Once the value of Pfi is known, then (6) can be rewritten in terms of known coefficients and the unknown output of the generators.

                                                  (8)

Where:

,,

 

SUMT method [3, 4]

The nonlinear programming problem can be formally stated as:

Minimise:f(x)                                                                                                              (9)

Subject to m linear and/or nonlinear equality constraints

            hi(x)=0i=1,2,…,m                                                                                          (10)

and  linear and/or nonlinear inequality constraints

gi(x)0, i=m+1,…,p                                                                                      (11)

The nonlinear programming algorithm SUMT [3] developed at the Research Analysis Corp., McLean, VA, is an extension of the “created response surface technique” proposed by Caroll, Fiabo and McCormick subsequently developed and validated the method and extended it to accommodate equality constraints. The SUMT algorithm has been developed to solve the nonlinear programming problem stated by Eqs. (9)- (11), in which the objective functions  and inequality constraints , can be nonlinear functions of the independent variables, but the equality constraints must be a linear function of the independent variables if convergence to the solution of the nonlinear programming problem is to be guaranteed.

The basic idea underlying SUMT is to solve repetitively a sequence of the unconstrained problems whose solutions at the limit approach the minimum of the version of SUMT the nonlinear programming problem. In 1967 coded version of SUMT the nonlinear programming problem is converted into a sequence of unconstrained problems by defining the  function as follows:

                                                     (12)

Where the weighting factors  are positive. Note that Fiacco and McCormich originally chose to make the function of the inequality constraints in the form of an added “barrier”:

For as one or more  from the feasible region, ; hence the concept of a barrier. As  is reduced, the effect of the barrier is reduced, and  may move closer to an inequality constraint boundary. As mentioned before, other possible choices exist for , such as:

.

Or                   .

and in the 1970 coded version of SUMT the penalty function used was:

                                       (13)

In both versions of the code the form of  chosen was simply the sum of the squares of the respective equality constraints, so that as , the equality constraints are more and more closely satisfied. Although in principle each equality constraint might be split up into two inequalities and treated as such, in practice this type of approach is quite unsatisfactory, it slows the search excessively and tends to cause premature termination.

The minimization of Eq.(12) or Eq.(13) is initiated at an interior point (or boundary point), that is, a point  at which all the inequality constraints are satisfied. After  is computed,  is determined by minimizing. Then  is computed and  determined by minimizing, and so forth.

The procedure described suffers from several handicaps. First, the Hessian matrix of the  function becomes progressively more ill-conditioned as the extreme is approached; hence the search directions may become mix-leading. Second, the rate of convergence depends on the initial choice of  and the method of reducing.

The summary of the computational procedure is as follows:

Step 1:

Step 2: compute where  and

Step 3:

Step 4:

Step 5:

Step 6:

Step 7: if 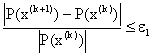 and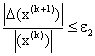

The problem becomes optimal and terminate the procedure. Otherwise, go to step 8.

Step 8: k=k+1 and go to step 2.

 

 

Application

 

The proposed method is applied to a model system to verify its effectiveness. The model system has three thermal units. Generators characteristics, that is, cost and emission coefficients, generation limits, and transmission loss using Bmn matrix are taken from [1].

The fuel cost equations in Rs/h for the three generators are

NOx emission equations in kg/h are

Generation limits in MW are

The loss coefficient matrix is

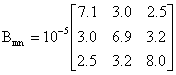
The SUMT algorithm is implemented by a software developed in “Turbo Pascal” language. For the power demand of 400 MW, the method is applied and the solutions obtained are given in table 1.

Table 1.  Summary of optimization process

 (Rs/kg)

 (MW)

 (MW)

 (MW)

 (MW)
44.8

100.27

151.28

148.52

7.15

 (Rs/h)

 (kg/h)

 (Rs/h)

Stage number

Computing time (s)

20515.77

193.84

29199.97

15

0.01

 

The convergences of total cost, fuel cost, NOx emission and power losses are illustrated in figures 1 to 4.

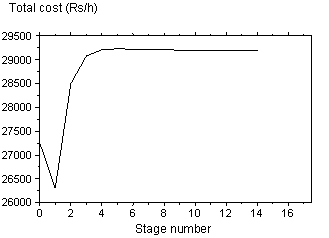
Figure 1. Total cost for power demand of 400 MW  

Figure 2. Fuel cost for power demand of 400 MW

 

Figure 3. NOx emission for power demand of 400 MW

 

Figure 4. Power losses for power demand of 400 MW

 

Figures 5 and 6 illustrate the total cost and NOx emission values associated with the power demand.

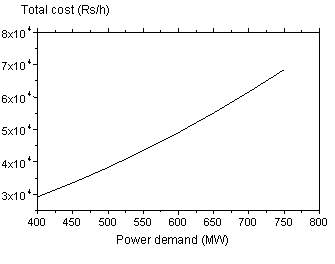
Figure 5. Total cost

Figure 6. NOx emission

 

It is clearly shown that total cost and NOx emission increase by increasing the power demand.

In order to demonstrate the performance of the proposed algorithm, a comparison for the power demand of 400 MW emerges between SUMT’method and other optimization methods [1], as is shown in figures 7, 8 and 9.

SUMT’ method.

CM : Conventional method.

SGA : Simple Genetic Algorithm.

RGA : Refined Genetic Algorithm.

                      

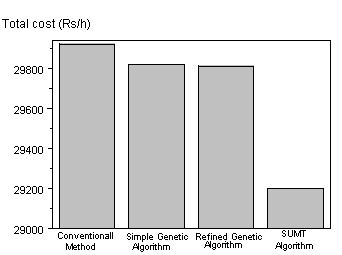
Figure 7. Comparison of total cost obtained from CM, SGA, RGA and SUMT' Method

 

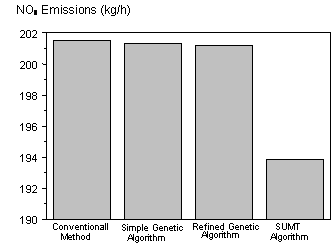
Figure 8. Comparison of NOx emission obtained from CM, SGA, RGA and SUMT' method

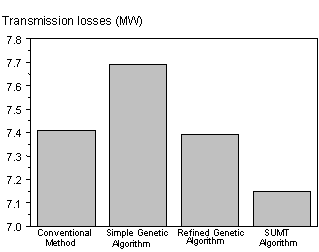
Figure 9. Comparison of transmission losses obtained from CM, SGA, RGA and SUMT' method

 

From the results, it is obvious that the proposed method is performing well in the solution of combined economic emission dispatch problem.

 

 

Conclusion

 

In this paper the combined economic emission dispatch problem is solving by SUMT method to minimize the fuel cost and NOx emission for a given load.

Satisfactory results are obtained by adapting the SUMT’method to three generators system and found that those results are very similar and even better to those obtained in [1]

Thus, the proposed algorithm is simple tool for the power industry to aid in curbing pollution and protect our environment.

 

 

References

 

1.            M. Sudhakaran, M. R.S. Slochanal, R. Sreeran, and N. Chandrasekhar, Application of refined genetic algorithm to combined economic and emission dispatch, IE (I) Journal-EL, Vol. 85, , pp. 115-119. 2004

2.            Bahman Kermanshahi, and Yoshimosa Aizowa, Genetic algorithm for coordination of environmental and economy objectives in ELD problem, Journal of Electrical Science and Technology, pp. 85-92. 1996

3.            M. Himmelblau, Applied non linear programming, McGraw-Hill, 1972.

4.            M.Rahli, P.Pirotte, Optimal load flow using sequential unconstrained minimization technique (SUMT) method under power transmission losses minimization, Electric Power Systems Research 52 61-64. 1999

5.            Y.Wallach.R.Even, Calculations and programs for power systems network, Prentice-Hall, Englewood, 1986.

6.            Chao-Ming Huang, Hong-Tzer Yang, and Chen-Lien Huang, Bi-objective power dispatch using fuzzy satisfaction maximizing decision approach, IEEE Transactions on Power Systems, Vol. 12, N°4, pp. 1715-1721.1997

7.            N.Kumarappan and M.R Mohan, Hybrid genetic algorithm based combined economic and emission dispatch for utility system, ICISIP, pp. 19-24. 2004