Generalized Predictive Control and Neural Generalized Predictive Control
Sadhana CHIDRAWAR1, Balasaheb PATRE1
Asst. Prof, MGM’s College of Engineering, Nanded (MS) 431 602
Professor, S.G.G.S. Institute of Engineering And Technology, Nanded (MS) 431 606
E-mail(s): sadhana_kc@rediff.com. bmpatre@yahoo.com
Abstract
As Model Predictive Control (MPC) relies on the predictive Control using a multilayer feed forward network as the plants linear model is presented. In using Newton-Raphson as the optimization algorithm, the number of iterations needed for convergence is significantly reduced from other techniques. This paper presents a detailed derivation of the Generalized Predictive Control and Neural Generalized Predictive Control with Newton-Raphson as minimization algorithm. Taking three separate systems, performances of the system has been tested. Simulation results show the effect of neural network on Generalized Predictive Control. The performance comparison of this three system configurations has been given in terms of ISE and IAE.
Keywords
Neural network; Model predictive control; GPC; NGPC.
Introduction
In recent years, the requirements for the quality of automatic control in the process industries increased significantly due to the increased complexity of the plants and sharper specifications of product quality. At the same time, the available computing power increased to a very high level. As a result, computer models that are computationally expensive became applicable even to rather complex problems. Intelligent and model based control techniques were developed to obtain tighter control for such applications.
In recent years, incorporation of neural networks as intelligent control techniques, to adaptive control system design has been claimed to be a new method for the control of systems with significant nonlinearities. Those neural network based control systems so far developed are generally classified as indirect or direct control methods.
Model predictive control (MPC) has found a wide range of applications in the process, chemical, food processing and paper industries. Some of the most popular MPC algorithms that found a wide acceptance in industry are Dynamic Matrix Control (DMC), Model Algorithmic Control (MAC), Predictive Functional Control (PFC), Extended Prediction Self Adaptive Control (EPSAC), Extended Horizon Adaptive Control (EHAC) and Generalized Predictive Control (GPC). In this work, among these number of MPC algorithms GPC is studied in detail.
Generalized Predictive Control (GPC)
The GPC method was proposed by Clarke et al [1] and has become one of the most popular MPC methods both in industry and academia. It has been successfully implemented in many industrial applications, showing good performance and a certain degree of robustness.
The basic idea of GPC is to calculate a sequence of future control signals in such a way that it minimizes a multistage cost function defined over a prediction horizon. The index to be optimized is the expectation of a quadratic function measuring the distance between the predicted system output and some reference sequence over the horizon plus a quadratic function measuring the control effort.
Generalized Predictive Control has many ideas in common with the other predictive controllers since it is based upon the same concepts but it also has some differences. As will be seen later, it provides an analytical solution (in the absence of constraints), it can deal with unstable and non-minimum phase plants and incorporates the concept of control horizon as well as the consideration of weighting of control increments in the cost function. The general set of choices available for GPC leads to a greater variety of control objective compared to other approaches, some of which can be considered as subsets or limiting cases of GPC.
The GPC scheme can be seen in Fig. 1. It consists of the plant to be controlled, a reference model that specifies the desired performance of the plant, a linear model of the plant, and the Cost Function Minimization (CFM) algorithm that determines the input needed to produce the plant’s desired performance. The GPC algorithm consists of the CFM block.
The GPC system starts with the input signal, r(t), which is presented to the reference model. This model produces a tracking reference signal, w (t) that is used as an input to the CFM block. The CFM algorithm produces an output, which is used as an input to the plant. Between samples, the CFM algorithm uses this model to calculate the next control input, u (t+1), from predictions of the response from the plant’s model. Once the cost function is minimized, this input is passed to the plant. This algorithm is outlined below.
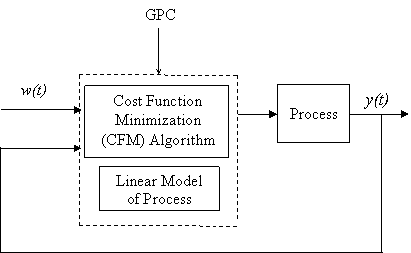
Figure 1. Basic Structure of GPC
Formulation of Generalized Predictive Control
Most single-input single-output (SISO) plants, when considering operation around particular set points and after linearization, can be described by Equation (1) [2].
![]() (1)
(1)
where
![]() and
and
![]() are
the control and output sequence of the plant and
are
the control and output sequence of the plant and ![]() is a zero mean white noise.
is a zero mean white noise. ![]() ,
,![]() And
And ![]() are the
following polynomials in the backward shift operator
are the
following polynomials in the backward shift operator ![]() :
:
![]()
![]()
![]()
Where, ![]() is the dead time of the system. This
model is known as a Controller Auto-Regressive Moving-Average (CARIMA) model.
It has been argued that for many industrial applications in which disturbances
are non-stationary an integrated CARMA (CARIMA) model is more appropriate. A
CARIMA model is given by Equation (2):
is the dead time of the system. This
model is known as a Controller Auto-Regressive Moving-Average (CARIMA) model.
It has been argued that for many industrial applications in which disturbances
are non-stationary an integrated CARMA (CARIMA) model is more appropriate. A
CARIMA model is given by Equation (2):
![]() (2)
(2)
with
![]()
For
simplicity, ![]() polynomial in Equation (2) is chosen to
be 1. Notice that if
polynomial in Equation (2) is chosen to
be 1. Notice that if ![]() can be truncated it can be absorbed
into
can be truncated it can be absorbed
into ![]() and
and![]() .
.
Cost Function
GPC algorithm consists of applying a control sequence that minimizes a multistage cost function of the form given in Equation (3)
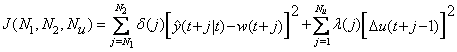 (3)
(3)
where
![]() is
an optimum j-step ahead prediction of the system output on data up to time k,
is
an optimum j-step ahead prediction of the system output on data up to time k,
![]() and
and
![]() are
the minimum and maximum costing horizons,
are
the minimum and maximum costing horizons, ![]() control horizon,
control horizon, ![]() and
and ![]() are
weighing sequences and
are
weighing sequences and ![]() is the future reference trajectory,
which can considered to be constant.
is the future reference trajectory,
which can considered to be constant.
The
objective of predictive control is to compute the future control sequence ![]() ,
, ![]() ,…
,…![]() in such a
way that the future plant output
in such a
way that the future plant output ![]() is driven close to
is driven close to ![]() . This is
accomplished by minimizing
. This is
accomplished by minimizing![]() .
.
Cost Function Minimization Algorithm
In order to optimize the cost function the optimal
prediction of ![]() for
for ![]() and
and ![]() is required. To compute
the predicted output, consider the following Diophantine Equation (4):
is required. To compute
the predicted output, consider the following Diophantine Equation (4):
![]() With
With ![]() (4)
(4)
The
polynomials ![]() and
and ![]() are uniquely defined with
degrees
are uniquely defined with
degrees ![]() and
and
![]() respectively.
They can be obtained dividing 1 by
respectively.
They can be obtained dividing 1 by ![]() until the remainder can be factorized
as
until the remainder can be factorized
as ![]() .
The quotient of the division is the polynomial
.
The quotient of the division is the polynomial![]() . An example demonstrating
calculation of Ej and Fj coefficients in Diophantine
Equation is shown in Example 1 below:
. An example demonstrating
calculation of Ej and Fj coefficients in Diophantine
Equation is shown in Example 1 below:
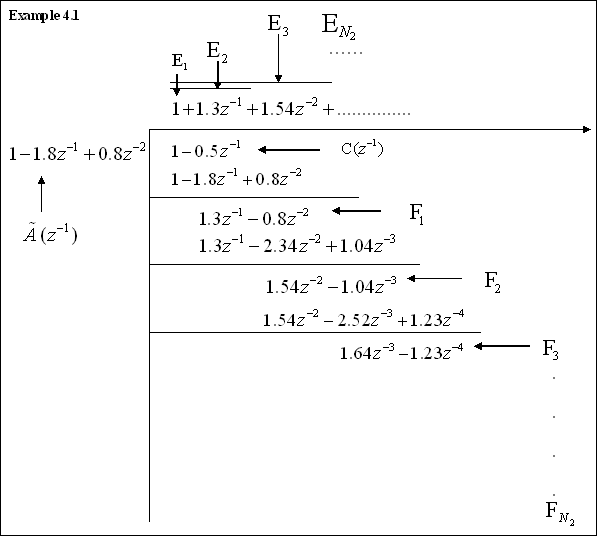
Example 1: Diophantine Equation Demonstration Example
Introduction to Neural Generalized Predictive Control
The ability of the GPC to make accurate predictions can be enhanced if a neural network is used to learn the dynamics of the plant instead of standard nonlinear modeling techniques. [3] The selection of the minimization algorithm affects the computational efficiency of the algorithm. Explicit solution for it can be obtained if the criterion is quadratic, the model is linear and there are no constraints; otherwise an iterative optimization method has to be used. In this project work Newton-Raphson method is used as the optimization algorithm. The main cost of the Newton-Raphson algorithm is in the calculation of the Hessian, but even with this overhead the low iteration numbers make Newton-Raphson a faster algorithm for real-time control [4].
The Neural Generalized Predictive Control (NGPC) system can be seen in Fig. 2. It consists of four components, the plant to be controlled, a reference model that specifies the desired performance of the plant, a neural network that models the plant, and the Cost Function Minimization (CFM) algorithm that determines the input needed to produce the plant’s desired performance. The NGPC algorithm consists of the CFM block and the neural net block.
![]()

Figure 2. Block Diagram of NGPC System
The NGPC system starts with the input signal, r(n), which is presented to the reference model. This model produces a tracking reference signal, ym(n), that is used as an input to the CFM block. The CFM algorithm produces an output that is either used as an input to the plant or the plant’s model. The double pole double throw switch, S, is set to the plant when the CFM algorithm has solved for the best input, u(n), that will minimize a specified cost function. Between samples, the switch is set to the plant’s model where the CFM algorithm uses this model to calculate the next control input, u(n+1), from predictions of the response from the plant’s model. Once the cost function is minimized, this input is passed to the plant. This algorithm is outlined below.
The computational performance of a GPC implementation is largely based on the minimization algorithm chosen for the CFM block. The selection of a minimization method can be based on several criteria such as: number of iterations to a solution, computational costs and accuracy of the solution. In general these approaches are iteration intensive thus making real-time control difficult. In this work Newton-Raphson as an optimization technique is used. Newton-Raphson is a quadratic ally converging. The improved convergence rate of Newton-Raphson is computationally costly, but is justified by the high convergence rate of Newton-Raphson.
The quality of the plant’s model affects the accuracy of a prediction. A reasonable model of the plant is required to implement GPC. With a linear plant there are tools and techniques available to make modeling easier, but when the plant is nonlinear this task is more difficult. Currently there are two techniques used to model nonlinear plants. One is to linearize the plant about a set of operating points. If the plant is highly nonlinear the set of operating points can be very large. The second technique involves developing a nonlinear model which depends on making assumptions about the dynamics of the nonlinear plant. If these assumptions are incorrect the accuracy of the model will be reduced.
Models using neural networks have been shown to have the capability to capture nonlinear dynamics. For nonlinear plants, the ability of the GPC to make accurate predictions can be enhanced if a neural network is used to learn the dynamics of the plant instead of standard modeling techniques. Improved predictions affect rise time, over-shoot, and the energy content of the control signal.
Formulation of NGPC
Cost Function
As mentioned earlier, the NGPC algorithm [4] is based on minimizing a cost function over a finite prediction horizon. The cost function of interest to this application is
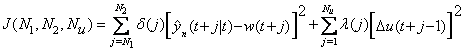 (5)
(5)
N1 = Minimum Costing Prediction Horizon
N2 = Maximum Costing Prediction Horizon
Nu= Length of Control Horizon
![]() = Predicted Output from Neural; Network
= Predicted Output from Neural; Network
![]() = Manipulated Input
= Manipulated Input
![]() = Reference Trajectory
= Reference Trajectory
δ and λ = Weighing Factor
This cost function minimizes not only the mean squared error between the reference signal and the plant’s model, but also the weighted squared rate of change of the control input with it’s constraints. When this cost function is minimized, a control input that meets the constraints is generated that allows the plant to track the reference trajectory within some tolerance. There are four tuning parameters in the cost function, N1, N2, Nu, and λ. The predictions of the plant will run from N1 to N2 future time steps. The bound on the control horizon is Nu. The only constraint on the values of Nu and N1 is that these bounds must be less than or equal to N2. The second summation contains a weighting factor, λ that is introduced to control the balance between the first two summations. The weighting factor acts as a damper on the predicted u (n+1).
Cost Function Minimization Algorithm
The objective of the CFM algorithm is to minimize J in Equation (6) with respect to [u(n+l), u(n+2), ..., u(n+Nu)]T, denoted U. This is accomplished by setting the Jacobian of Equation (5) to zero and solving for U. With Newton-Rhapson used as the CFM algorithm, J is minimized iteratively to determine the best U. An iterative process yields intermediate values for J denoted J(k). For each iteration of J(k) an intermediate control input vector is also generated and is denoted as in Equation (6):
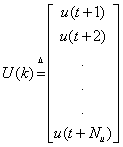
![]() k=1,……Nu (6)
k=1,……Nu (6)
Newton-Raphson method is one of the most widely used of all
root-locating formula. If the initial guess at the root is xi,
a tangent can be extended from the point [xi, f(xi)].
The point where this tangent crosses the x-axis usually represents an
improved estimate of the root. So the first derivative at x on
rearranging can be given as:![]()
Using this Newton-Raphson update rule, U(k+1) is given by Equation (7)
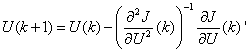
Where ![]() (7)
(7)
And the Jacobian is denoted as in Equation (8)
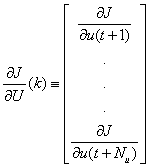 (8)
(8)
And the Hessian as in Equation (9)
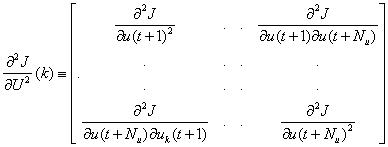 (9)
(9)
Each element of the Jacobianis calculated by partially differentiating Equation (8) with respect to vector U.
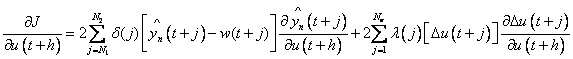 (10)
(10)
Where,
![]()
Once again Equation (10) is partially differentiated with respect to vector U to get each element of the Hessian.
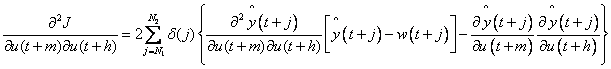
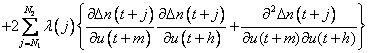 (11)
(11)
The ![]() elements of the Hessian matrix in
Equation (11) are
elements of the Hessian matrix in
Equation (11) are![]() .
.
The last computation needed to evaluate ![]() is the calculation
of the predicted output of the plant,
is the calculation
of the predicted output of the plant,![]() , and it’s derivatives. The next
sections define the equation of a multilayer feed forward neural network, and
define the derivative equations of the neural network.
, and it’s derivatives. The next
sections define the equation of a multilayer feed forward neural network, and
define the derivative equations of the neural network.
Neural Network Architecture
In NGPC the model of the plant is a neural network. This neural model is constructed and trained using MATLAB Neural Network System Identification Toolbox commands [5].
The output of trained neural network is
used as the predicted output of the plant. This predicted output is used in the
Cost Function Minimization Algorithm. If yn(t) is the neural
network’s output then it is nothing but plant’s predicted output ![]() .
.
The initial training of the neural network is typically done off-line before control is attempted. The block configuration for training a neural network to model the plant is shown in Fig. 3. The network and the plant receive the same input, u(t). The network has an additional input that either comes from the output of the plant, y(t), or the neural network’s, yn(t). The one that is selected depends on the plant and the application. This input assists the network with capturing the plant’s dynamics and stabilization of unstable systems. To train the network, its weights are adjusted such that a set of inputs produces the desired set of outputs. An error is formed between the responses of the network, yn(t), and the plant, y(t). This error is then used to update the weights of the network through gradient descent learning. In this work a Levenberg-Marquardt method is used as gradient descent learning algorithm for updating the weights. This is standard method for minimization of mean-square error criteria, due to its rapid convergence properties and robustness. This process is repeated until the error is reduced to an acceptable level.
Since a neural network will be used to model the plant, the configuration of the network architecture should be considered. This implementation of NGPC adopts input/output models.
u(t) s y(t) z-1 Neural Plant Model
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()

![]()
Figure 3. Block Diagram of Off-line Neural Network Training
The diagram below, Fig.4, depicts a multi-layer feed-forward neural network with a time-delayed structure. For this example, the inputs to this network consists of two external inputs, u(t) and two outputs y(t-1), with their corresponding delay nodes, u(t), u(t-1) and y(t-1), y(t-2). The network has one hidden layer containing five hidden nodes that uses bi-polar sigmoidal activation output function. There is a single output node which uses a linear output function, of one for scaling the output.
Y(t-1) Y(t-2) U(t) U(t-1)
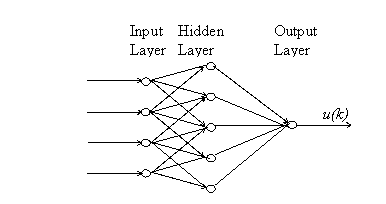
Figure 4. Neural Network Architecture
The equation for this network architecture is:
![]()
And
![]() (12)
(12)
Where,
![]() is the
output of the neural network
is the
output of the neural network
![]() is the
output function for the
is the
output function for the ![]() node of the hidden layer
node of the hidden layer
![]() is the
activation level of the
is the
activation level of the ![]() node’s output function
node’s output function
![]() is
the number of hidden nodes in the hidden layer
is
the number of hidden nodes in the hidden layer
![]() is
the number of input nodes associated with
is
the number of input nodes associated with ![]()
![]() is
the number of input nodes associated with
is
the number of input nodes associated with ![]()
![]() is
the weight connecting the
is
the weight connecting the ![]() hidden node to the output node
hidden node to the output node
![]() is
the weight connecting the
is
the weight connecting the ![]() hidden input node to the
hidden input node to the ![]() hidden node
hidden node
![]() is the
delayed output of the plant used as input to the network
is the
delayed output of the plant used as input to the network
![]() is the
input to the network and its delays
is the
input to the network and its delays
This neural network is trained in offline condition with plants input/output data
Prediction Using Neural Network
The NGPC algorithm uses the output of the plant's model to predict the plant's dynamics to an arbitrary input from the current time, t, to some future time, t+k. This is accomplished by time shifting equations Equation (11) and (12), by k, resulting in Equation (13) and (14).
![]() (13)
(13)
And
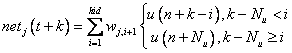
![]() (14
(14
![]()
The first summation of Equation (14) breaks the input into
two parts represented by the conditional. The condition where ![]() handles the
previous future values of the
handles the
previous future values of the ![]() up to
up to ![]() . The condition where
. The condition where ![]() sets the
input from
sets the
input from ![]() to
to ![]() equal to
equal to ![]() . The second
condition will only occur if
. The second
condition will only occur if ![]() . The next summation of Equation (14) handles
the recursive part of prediction. This feeds back the network output,
. The next summation of Equation (14) handles
the recursive part of prediction. This feeds back the network output,![]() , for
, for ![]() or
or ![]() times,
which ever is smaller. The last summation of Equation (14) handles the previous
values of y. The following section derives the derivatives of Equation
(13) and (14) with respect to the input
times,
which ever is smaller. The last summation of Equation (14) handles the previous
values of y. The following section derives the derivatives of Equation
(13) and (14) with respect to the input![]() .
.
Neural Network Derivative Equations
To evaluate the Jacobian and the Hessian in Equation (8) and (9) the network’s first and second derivative with respect to the control input vector are needed.
Jacobian Element Calculation
The elements of the Jacobian are obtained by differentiating yn(t+k) in Equation (13) with respect to u(t+h) resulting in
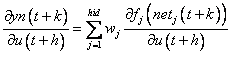 (15)
(15)
Applying chain rule
to![]() results in
results in
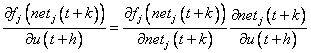 (16)
(16)
Where ![]() is the output function’s derivative
which will become zero as we are using a linear (constant value) output
activation function and
is the output function’s derivative
which will become zero as we are using a linear (constant value) output
activation function and
 (17)
(17)
![]()
Note that in the last summation of Equation (17) the step function, δ, was introduced. This was added to point out that this summation evaluates to zero for k-i<l, thus the partial does not need to be calculated for this condition.
Hessian Element Calculation
Hessian elements are obtained by once again differentiating Equations (15) by u(t+m), resulting in Equation (18):
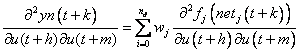 (18)
(18)
Where,
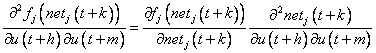 (19)
(19) 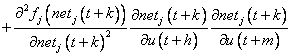
Equation (19) is the result of applying the chain rule twice
Simulation Results
The objective of this study is to show how GPC and NGPC implementation can cope with linear systems. GPC is applied to the systems with changes in system order. The Neural based GPC is implemented using MATLAB Neural Network Based System Design Toolbox. [5].
GPC and NGPC for Linear Systems
The above derived GPC and NGPC algorithm is applied to the different linear models with varying system order, to test its capability. Carrying out simulation in MATLAB 7.0.1 does this. Different systems with large dynamic differences are considered for simulation. GPC and NGPC are showing robust performance for these systems. In below figures, for every individual system the systems output with GPC and NGPC is plotted in single figure for comparison purpose. Also the control efforts taken by the both controllers are plotted in consequent figures for every individual figure.
In this simulation, neural network architecture considered is as follows. The inputs to this network consists of two external inputs, u(t) and two outputs y(t-1), with their corresponding delay nodes, u(t), u(t-1) and y(t-1), y(t-2). The network has one hidden layer containing five hidden nodes that uses bi-polar sigmoid activation output function. There is a single output node that uses a linear output function, of one for scaling the output.
For all the systems Prediction Horicon N1 =1, N2 =7 and Control Horizon (Nu) is 2. The weighing factor λ for control signal is kept to 0.3 and δ for reference trajectory is set to 0. The same controller setting is used for all the systems simulation. The following simulation results are obtained showing the Plant output when GPC and NGPC are applied. Also the required Control action for different systems is shown.
System I: The GPC and NGPC algorithms are applied to a second order system given in Equation (20). Fig. 5 shows the plant output when GPC and NGPC. Fig. 6 shows the control efforts taken by both controllers.
![]() (20)
(20)
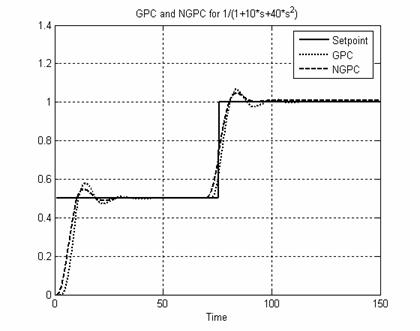
Figure 5. System I Output using GPC and NGPC
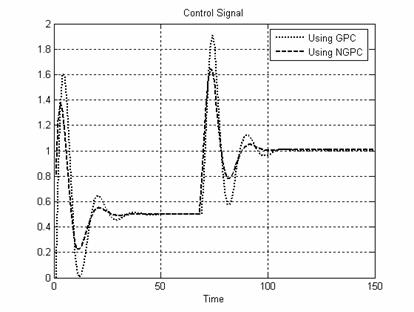
Figure 6. Control Signal for System I
System II A simple first order system given by Equation (21) is controlled. Fig. 7 and Fig. 8 show the system output and control signal.
![]() (21)
(21)
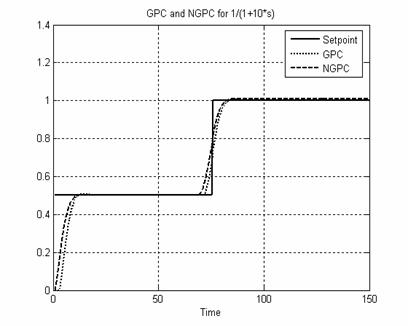
Figure 7. System II Output using GPC and NGPC
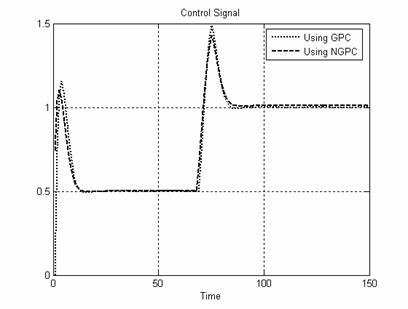
Figure 8. Control Signal for System II
System III: A second order system given by Equation (22) is controlled using GPC. Fig. 9 and Fig10show the predicted output and control signal.
![]() (22)
(22)
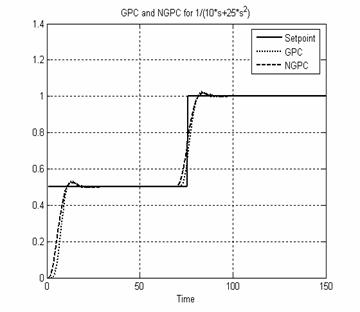
Figure 9. System III Output using GPC and NGPC
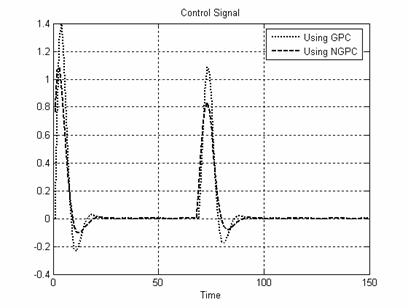
Figure 10. Control Signal for System III
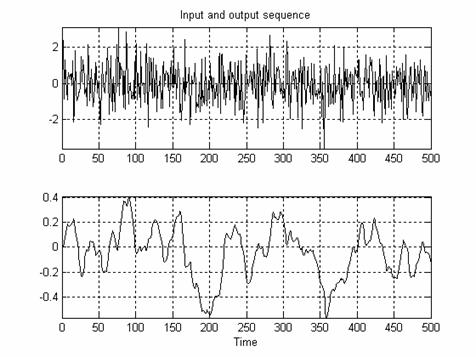
Before applying NGPC to the all above systems it is initially trained using Levenberg-Marquardt learning algorithm. Fig. 10(a) shows Input data applied to the neural network for offline training purpose. Fig. 10(b) shows the corresponding neural network output.
Figure 10 (b). Neural Network
Response for Random Input Figure 10 (a). Input Data for Neural Network Training
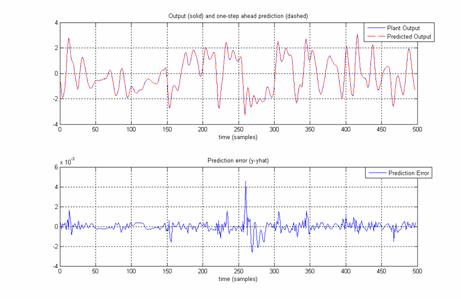
To check whether this neural network is trained to replicate it as a perfect model or not, common input is applied to the trained neural network and plant. Fig. 11(a) shows the trained neural networks output & predicted output for common input. Also the error between these two responses is shown in Fig. 11(b).
Figure
11(b). Error between Neural Network & Plant
Output Figure
11(a). Neural Network & Plant Output
Performance evaluation of both the controller is carried out using ISE and IAE criteria given by the following equations:

Table 1 gives ISE and IAE values for both GPC and NGPC implementation for all the linear systems given by Equation 20 to Equation 21. We can find that for each system ISE and IAE for NGPC is smaller or equal to GPC. So using GPC with neural network i.e. NGPC control configuration for linear application, is also a better choice.
Table 5.1: ISE and IAE Performance Comparison of GPC and NGPC for Linear System
|
Systems |
Setpoint |
GPC |
NGPC |
||
|
ISE |
IAE |
ISE |
IAE |
||
|
System I |
0.5 |
1.6055 |
4.4107 |
1.827 |
3.6351 |
|
1 |
0.2567 |
1.4492 |
0.1186 |
1.4312 |
|
|
System II |
0.5 |
1.1803 |
3.217 |
0.7896 |
2.6894 |
|
1 |
0.1311 |
0.767 |
0.063 |
1.017 |
|
|
System III |
0.5 |
1.4639 |
3.7625 |
1.1021 |
3.3424 |
|
1 |
0.1759 |
0.9065 |
0.0957 |
0.7062 |
|
|
1 |
0.1311 |
0.767 |
0.063 |
1.017 |
|
Conclusion
In this paper a conventional Generalized Predictive Control algorithm is derived in detail. The capability of the algorithm is tested on variety of systems. An efficient implementation of GPC using a multi-layer feed-forward neural network as the plant’s nonlinear model is presented to extend the capability of GPC i.e. NGPC for controlling linear process very efficiently.
References
1. D. W. Clarke, C. Mohtadi and P. S. Tuffs, Generalized predictive control-part I. the basic algorithm, Automatica, vol 23, pp. 137-148. 1987
2. Jacek M. Zurada, Introduction to Artificial Neural Systems, Jaico Publishing House, 2006.
3. Xue-Mei Sun, Chang-Ming Ren, Pi-Lian He, Yu-Hong Fan, Predictive control based on neural network for nonlinear system with time delays, IEEE proceeding , , pp. 319-322. 2002
4. Donald Soloway, Neural generalized predictive control, Proceeding IEEE International Symposium on Intelligent Control, Dearborn, , pp. 277-282. 1996
5. M. Nørgaard, Neural Network Based Control System Design Toolkit, ver.2 Tech. Report. 00-E-892, Department of Automation, Technical University of Denmark, 2000.
6. E. P. Nahas, M. A. Henson, D. E. Seborg, Nonlinear internal model control strategy for neural network models, Computers Chemical Engineering, vol.16, pp. 1039-1057. 1992.