Extrinsic and Intrinsic Effects in Photon Induced K X-Ray Satellite Spectra of Al and Al2O3
Sanjay KUMAR SRIVASTAVA and Amar BAHADUR*
Department of Physics, Kamla Nehru Institute of Physical and Social Sciences, Sultanpur, 228118, INDIA
*E-mail: amarknipss@gmail.com
Abstract
The origin of KaL1 and KaL2 satellite spectra of Al and Al2O3 have been explained using plasmon theory with new approach by considering relative interference between intrinsic and extrinsic effects. The results have been probed by comparing to the relative satellite yields obtained by photo- ionization and other experimental estimates. We also review existing calculations and measurements found that these satellites are due to surface plasmon excitations.
Keywords
X-ray satellites; Energy separation; Surface plasmon; Extrinsic and intrinsic effects; relative intensity.
Introduction
The origins of collective oscillations of free electron gas in solids are well known since early days of X- ray photoemission spectroscopy [1-19]. In a pioneered theoretical investigation, Bohm and Pine [20] suggested that electrons are not entirely free in an electron gas as concluded by Sommerfeld [21] but these are free within the Debye length. Generally speaking, this electron gas or sea of conduction electrons refers to the bulk of material which has properties that allow the assumption of condition electrons acting as a free electron gas. Beyond Debye length they behave collectively and oscillate with frequency called plasma frequency ωp = (4πne2/m)1/2 where n = electron density, m = effective mass of electrons, e = charge of electron. These collective oscillations of free electron gas are called plasma oscillation [22]. Bohm and Pine [23] also suggested that during x- ray photoemission process (XPS) the solid absorbs an incident photon and emits an electron form the core level. The out going electron may suffer energy losses before escaping out of the material. This energy loss process is quantized and quantum of energy is called plasmon. Thus the energy loss spectrum (ELS) shows zero loss peak centered at E0 and satellite peak at E0 -ħωp, E0 -2ħωp, E0 -3ħωp etc., where ħωp is plasmon energy. The emission line owing to this process is called Low Energy Satellites. However if plasma pre-exist, then during x-ray photoemission process it can transfer its energy to the transiting photoelectron before escaping out of the material. Thus the energy of emitted photoelectron will be higher than the energy of main peak E0 by an amount equal to the plasmon energy and satellites are observed at an enrgy separation E0 +ħωp, E0 +2ħωp, E0 +3ħωp etc. The emission line owing to this process is called High Energy Satellites.
Recently, P. Suresh et.al. [24] have observed several satellites on high energy side of main line employing photon excitation and assigned the origin of these satellite using molecular orbital approach. However in a comparison between the experimental [25-29] and calculated [30] results one can observe the major differences. Although the origin of these satellites can be explained by different theoretical models, but plasmon excitation model is most suitable model for all the satellites which are observed in plasmon energy range (4ev to 20eV). In the present paper we have explained the origin of KaL1 and KaL2 satellites of Al using plasma oscillation theory with new approach by considering intrinsic and extrinsic effects simultaneously.
Plasma oscillations are two types- Bulk plasmon and Surface plasmon. Bulk plasmons are longitudinal oscillation mode of the electron gas in the solid and are given by condition ε =0, where ε is bulk dielectric function. The collective oscillations of electron gas on the interface between a metal and dielectric are known as surface plasmons. Surface plasmons are an oscillating sheet of charge located at the surface, although its energy is associated by bulk property ε = -1. Satellites can be bulk plasmon satellites or surface plasmon satellites depending upon whether plasma oscillations are excited in the bulk or near the surface. Langreth [13] has pointed out, when the surface effect is more important than bulk and vice versa. The energy of bulk plasmon is given by Marton et.al. [31] as bulk plasmon energy:
(ħwp) = 28.8 (Z's/W)1/2 (eV) (1)
Where Z' = effective number of electrons taking place in plasma oscillation, s = specific gravity of compounds, W = molecular weight of compounds. Since at the surface more a localized oscillation can occur with frequency ωs and also depending upon conditions and the energy of corresponding peak, surface plasmon may also be seen. Hence we also surface plasmon energy using formula given by Ritchie [32] as-
Surface plasmon energy
(ħws) = ħwp /√2 (eV) (2)
Table1. Calculation of surface plasmon energy (eV).
|
Satellites |
Metal/ Compounds |
Z' |
s |
W |
Calculated plasmon energy |
Experimental energy separation |
|
KaL1 |
Al |
3 |
2.7 |
26.98 |
11.2 ( ħws) |
10.5±0.02 [24] 9.4[33] |
|
KaL2 |
Al |
- |
- |
26.98 |
22.3 (2ħws) |
21.0±0.02[24]20.6[33] |
|
KaL1 |
Al2O3 |
8 |
3.97 |
101.96 |
11.4 (ħws) |
11.6 ±0.02 [24] |
|
KaL2 |
Al2O3 |
- |
- |
101.96 |
22.7 (2ħws) |
23.1 [33] |
Intrinsic and Extrinsic effects
Our calculated values of surface plasmon energy agree well with the observed values but in order to further confirm the involvement of plasmon we also calculated the relative intensity of these satellites using plasmon theory in new light. The physics of plasma excitation in photoemission is very interesting because different processes contribute to its intensity. The sudden change in the potential due to formation of a core hole attracts the conduction electrons to screen the core- hole resulting, in the intrinsic plasmon [34] excitation. On the other hand, the extrinsic plasmon excitation is created by the Coulomb interaction of the conduction electrons with the photoelectron traversing through the solid form the photoemission site to the surface. The interference effect can also be visualizes as the interaction between localizes photohole (intrinsic) and the outgoing photoelectron (extrinsic) in which the virtual plasmon created by one is absorbed by the other. It has been observed that both the contributions of both intrinsic and extrinsic plasmon excitations in photoemission spectrum overlap one another, so they are not be readily separable experimentally. Also the question whether the photoemission satellite spectra seen are intrinsic or extrinsic in nature has aroused much controversy. Thus in order to analyze the spectrum a more detailed qualitative analysis is needed. Many theoretical studies have been performed to evaluate the contribution of the intrinsic and extrinsic processes and to understand their origin in photoemission. Lundquist [1] suggested that over 50% of the loss spectrum is due to the intrinsic processes, while a more recent semi- phenomenological analysis by Pardee et al. [3] indicated 10% or less for Al. Sunjic et al. [14-15] argued that photoemission is a many- body process and thus the breakdown into intrinsic and extrinsic effects is artificial. In ref.[35] it is suggested that the extrinsic effect should always be of major importance for free-electron like materials since the probability for electron- plasmon scattering in these materials is relatively high for almost any electron kinetic energy. Chang et al. [10] estimated that the intrinsic plasmon production associated with the core hole is quite small including the interferences between the core hole and outgoing electron. The analysis of the intensity profiles of the plasmon loss structure in XPS spectrum for Al indicates that the extrinsic effects contribute the major part. Feibelman [12] calculated the plasmon intensities as a function of depth and θ, assuming an infinite vector. Penn [16] calculated the plasmon line-shapes and estimated the intrinsic bulk plasmon contribution to be 26% for Al, which was much lower than 50% intrinsic plasmon contribution suggested by Lundqvist [1].
Inglesfield [17-18] studied the suppression of the plasmon intensities at low electron kinetic energy by calculating the plasmon line shapes as function of the kinetic energy and depth of photoemission site. Inglesfield [18] used the golden rule formalism of photoemission and considered plasmon dispersion as well as the interference effect. The interference between extrinsic and intrinsic plasmon was found to suppress the long wavelength plasmon excitations. Using a transition- matrix approach, Bose et. al. [36] calculated the line shape and intensity of the intrinsic, extrinsic and interference contributions to both bulk and surface plasmons as function of z, and their results are in good agreement with that of Inglesfield [18]. The theoretical calculations by different groups predict an asymmetric line- shape for both bulk and surface plasmon [16-18, 36-37]. Although plasmon excitations in photoemission spectra of Al have been known for more than three decades and were studied by different groups in the late 1970 and early 1980s, yet the explanation of satellite intensity remained unresolved. Now in the present paper we have tried tackle this longstanding problem and tried to incorporate both the processes i.e. the relative contribution of extrinsic process as well as intrinsic process. Intrinsic process is further divided into two categories [38]. (a) When number of slow electrons is conserved; plasmon satellites are weak and (b) when number of electrons is not conserved; plasmon satellites are strong. We have calculated relative intensity in both the cases with new modification in the light of Bradshaw [38] and Lengreth [2] work, which explains that not only intrinsic process but extrinsic process and their relative contribution may also contribute in relative intensities. The combined effect of intrinsic and extrinsic plasmon excitation intensity variation was suggested by Lengreth [13] as:
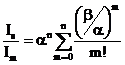 (3)
(3)
The value of β [39] is taken as β = 0.12rs which is purely intrinsic, rs = (47.11/ ħws) 2/3 is dimensionless parameter [40] and α = 0.47 rs1/2 [41-46] in the place of α = (1+l/L)-1 used by Pardee et. al. [3]. The equation (3) contains a series of terms. The first term of the equation is purely extrinsic, while second term is purely intrinsic. The other terms are containing the relative contributions of both extrinsic and intrinsic. The specialty of this formula is that each term alone or simultaneously with other terms is able to give the relative intensity. This formula also includes both the categories mentioned by Bradshaw [38] and gives better results as compared than traditional methods for calculation of the relative intensity. Using the values of α, β and rs in equation (3) we calculated the relative intensity of satellites as given is Table 2.
Table 2. Relative intensity of satellites (%)
|
Satellites |
Metal or Compounds |
rs |
α |
β |
Intensity assignments |
Relative intensity |
|
|
Calculated |
Experimental |
||||||
|
KaL1 |
Al |
2.61 |
0.76 |
0.31 |
β2/2α+ β3/6α2 |
0.074 |
0.099±0.0009 [24] 0.107 [25] 0.08 [26] 0.11 [26] 0.09 [This study] 0.10 [This study] 0.101 [27] 0.107 [28] 0.117 [29] 0.105 [30] |
|
KaL2 |
Al |
2.07 |
0.68 |
0.25 |
β3/6α |
0.004 |
0. 0056±0.0006 [24] 0.011 [25] 0.01 [29] 0.007 [30] |
|
KaL1 |
Al2O3 |
2.58 |
0.75 |
0.31 |
β2/2α+ β3/6α2 |
0.072 |
0.114±0.01 [24] 0.123 [25] 0.119 [27] 0.119 [28] |
|
KaL2 |
Al2O3 |
2.05 |
0.67 |
0.25 |
β3/6α |
0.0037 |
0.0079±0.0008[24] |
Conclusion
The presented calculated energy separation of high energy satellites KaL1 (also KaL2) of diagram line KaL0 compare well with the values reported P. Suresh et.al. [24] using photon excitation (Rh tube x-rays) and theoretically calculated by Maruer and Wastson [33] within experimental errors. The KaL1 satellites are due to single plasmon excitation, while KaL2 satellites are due to double plasmon excitation. Our calculated values of relative intensity of Al and Al2O3 (see table-2) also compare well with values observed by P. Suresh et.al. [24] using photon excitation (Rh tube x-rays), Utiainen et.al. [25] employing photon excitation (Cr tube x-rays), Bonnelle Ch and Senemaud [26] employing photon excitation (Ag, MO L x-rays) and theoretical results by T. Aberg [30]. Hence we conclude that satellites of Al and Al2O3 are due to relative interference of intrinsic and extrinsic effects.
Acknowledgement
Authors would acknowledge Prof. K. S. Srivastava (Physics Department, Lucknow University, Lucknow U.P.) and Dr. A. K. Srivastava (Head, Department of Physics, Kamla Nehru Institute of Physical and Social Sciences, Sultanpur) for their guidance and valuable suggestions.
References
1. B. I. Lundqvist, Phys. Kondens. Mater., 236, 9, 1969.
2. D. C. Lengreth, Phys. Rev. Letter, 26, 1229, 1971.
3. W. J. Pardee, G.D. Mahan, D. E. Eastman, R.A. Pollak, L. Ley, F.R. McFeely, S.P. Kowalczky and D.A. Shirely, Phys. Rev. B, 11, 3614, 1975.
4. J. C. Fuggle, D.J.Febian and L.M. Waston, Journal of Elect. Secpectroscopy and Related Phenomenon, 9, 99, 1976.
5. P. M. Th. van Attekum and J.M. Trooster, Phys. Rev. B, 18, 3872, 1978.
6. A.M. Bradshaw, W. Domcke, and L.S. Cederbaum, Phys. Rev. B, 16, 1480, 1977.
7. R. J. Baird, C.S. Fadley, S.M. Goldberg, P. J. Febelman and M. Sunjific, Surface Science, 72, 495, 1978.
8. Y. Baer and G. Busch, Phys. Rev. Letter, 30, 280, 1973.
9. D. Norman and D. P. Woodruff, Surface Science, 79, 76, 1979.
10. J. J. Chang and D. C. Lengreth, Phys. Rev. B, 5, 3512, 1972.
11. G. D. Mahan, Phys. Status Solidi B, 55, 703, 1973.
12. Peter. J. Feibelman, Phys. Rev. B, 7, 2305, 1973,
13. D. C. Lengreth, Collective Properties of Physical Systems, edited by B. Lundquist and S. Lunduquist (Academic Press New York, 1974) p.210.
14. M. Sunjic, D. Sokcevis and A. Lucas, Journal of Electron Secpectroscopy and Related Phenomenon, 5, 963, 1974.
15. Sunjic, M. and Sokcevic, D., Solid State Commun., 1974, 15, 165;
16. D. R. Penn, Phys. Rev. Letter, 38, 1429, 1977.
17. J. E. Iglesfield, Solid State Communications: Solid State Phys. 40, 467, 1981.
18. J. E. Iglesfield, J. Phys. C, 16, 403, 1983.
19. L. H. Hedin, X-Ray Spectroscopy, (Ed. by L. V. Azaroff), McGraw-Hill, New York, p. 226, 1974,
20. D. Pines and D. Bohm, Phys. Rev. 85, 338, 1952.
A. Sommerfeld, Z. Phys. 47, 1, 1928.
21. D. Pines, Elementary Excitations in Solids, Benjamin, New York, 1964, p. 92.
22. D. Pines and D. Bohm, Phys. Rev. 92, 609, 1953.
23. P Suresh, B.Seetharami Reddt, T Seshi Reddy, M. L. N. Raju, B.V. Thirumala Rao, B Malliikarajuna Rao and M.V. R. Murti, J. Phys. B: At. and Mol. Opt. Phys. 33, 1665, 2000.
24. J. Utriainen, M. Linkoaho, E. Rantavuori, T. Aberg and G. Graeffe, Z. Naturf. 23A, 1187, 1968.
25. Bonnelle Ch and Senemaud Ch C. R. Acad. Sci. Paris. 268, 65, 1969.
26. W. L. Baun and D.W. Fischer, Advanced In X- ray analysis 8, (New York, Plenum) p. 371.
27. V. F. Demekhin and V.P. Sachenko, 1967, Bull. Advanced Sci. USSR, Phys. Scr. 31, 921.
28. M.O. Kraus, J.G. Ferreira, J. Physique, 88, 2007, 1975.
29. T. Aberg , Phys. Lett. 26, 515, 1968.
30. L. Marton, L. B. Leder and H. Mendlowitz, Advanced in electronic and electron phys. (Ed. by L. Marton) New York, Academic Press, 1955, p.183.
31. R. H. Ritchie, Phys. Rev.106, 874, 1957.
32. R. J. Maurer and R.L.Waston, At. Data Nucl. Data Tables, 34, 185, 1986.
33. S. Hufner, Photoelectron Spectroscopy Springer, Berlin, Springer, 1995.
34. C. J. Tung and R. H. Ritchie, Phys, Rev. B l6, 4302, 1977.
35. S. M. Bose, S. Prutzer, and P. Longe, Phys. Rev. B, 27,5992, 1983.
36. L.H. Hedin, In X-ray Spectroscopy, New York (ed. Azaroff, L. V.), McGraw-Hill, 1974.
A. M. Bradshaw, Cederbaurn S.L, Domeke W. & Krause Jour. Phys C: Solid State Phys. 7, 4503, 1974.
37. K. S. Srivastava, K.Sinha, A. K. Srivastava, Sameer Sinha, S. K. Shukla, M.N. Sharma, D. K.Singh, and S.K. Srivastava, Indian Jour. of Pure and Applied Physics, 34, 190, 1996.
38. K. S. Srivastava, Shiv Singh, A.K. Srivastava, R. S. Nayal, A. Chaubey, and P. Gupta, Phys. Rev. A 25, 2838, 1982.
39. S. K. Srivastava, Amar Bahadur and Pankaj Kumar Singh, Material Science: (an Indian Journal) 4, 119, 2008.
40. S. K. Srivastava, Amar Bahadur and Pankaj Kumar Singh, Material Science: (an Indian Journal) 4, 117, 2008.
41. S. K. Srivastava, Amar Bahadur, Sanjeet Pratap Singh and Arun Kumar Singh, Ultra Science, 20, 587, 2008.
42. S. K. Srivastava, Amar Bahadur, Fizika A, 17, 117, 2008.
43. S. K. Srivastava, Amar Bahadur and Pankaj Kumar Singh, Ultra Science, 20, 315, 2008.
44. S. K. Srivastava, Amar Bahadur and Pankaj Kumar Singh, Leonardo Journal of Sciences, 13, 39, 2008.