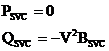Voltage Stability Improvement using Static Var Compensator in Power Systems
Mark Ndubuka NWOHU
Department of Electrical/Computer Engineering, Federal University of Technology, Minna, Niger State, Nigeria
E-mail: mnnwohu@yahoo.com
Abstract
This paper investigates the effects of Static Var Compensator (SVC) on voltage stability of a power system. The functional structure for SVC built with a Thyristor Controlled Reactor (TCR) and its model are described. The model is based on representing the controller as variable impedance that changes with the firing angle of the TCR. A Power System Computer Aided Design /Electromagnetic Transients including DC (PSCAD/EMTDC) is used to carry out simulations of the system under study and detailed results are shown to access the performance of SVC on the voltage stability of the system.
Keywords
Thyristor; Transmission; Simulations; Stability; Voltage.
Introduction
Today’s changing electric power systems create a growing need for flexibility, reliability, fast response and accuracy in the fields of electric power generation, transmission, distribution and consumption. Flexible Alternating Current Transmission Systems (FACTS) are new devices emanating from recent innovative technologies that are capable of altering voltage, phase angle and/or impedance at particular points in power systems. Their fast response offers a high potential for power system stability enhancement apart from steady-state flow control. Among the FACTS controllers, Static Var Compensator (SVC) provides fast acting dynamic reactive compensation for voltage support during contingency events which would otherwise depress the voltage for a significant length of time. SVC also dampens power swings and reduces system losses by optimized reactive power control. Power System Computer Aided Design/Electromagnetic Transients Direct Current (PSCAD/EMTDC) has been used in this paper to conduct simulations on voltage regulation at the point of connection of SVC to the system.
However, the aim of this paper is to enhance voltage stability using Static Var Compensator at the event of occurrence of fault in the system.
Model of SVC with PSCAD Representation of Its Control
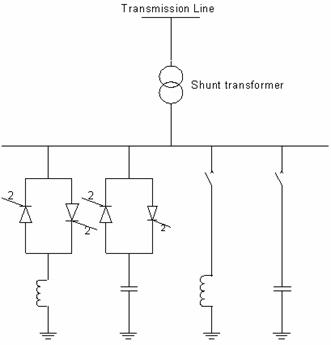
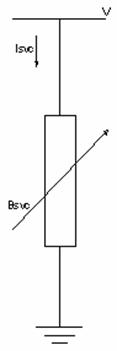
In order to investigate the impact of SVC on power systems, appropriate SVC model is very important. In this section, SVC and its mathematical model will be introduced. SVC is built up with reactors and capacitors, controlled by thyristor valves which are in parallel with a fixed capacitor bank. It is connected in shunt with the transmission line through a shunt transformer and thus, represented in Figure 1 [1]. Figure 2 shows the equivalent circuit at which SVC is modeled [2, 3].
|
|
|
|
Figure 1. Functional diagram of SVC |
Figure 2. Equivalent circuit of SVC |
The model considers SVC as shunt-connected variable susceptance, BSVC which is adapted automatically to achieve the voltage control. The equivalent susceptance, Beq is determined by the firing angle α of the thyristors that is defined as the delay angle measured from the peak of the capacitor voltage to the firing instant. The fundamental frequency equivalent neglecting harmonics of the current results in [4]:
|
|
(1) |
where
|
|
If the real power consumed by the SVC is assumed to be zero, then:
|
|
(2) |
where V is the bus voltage magnitude.
As the reactive power demand at the bus varies, the susceptance is varied subject to the limits. However, the reactive power is a function of the square of the bus voltage. Hence the reactive power generated decreases as the voltage decreases.
Svc Control Scheme
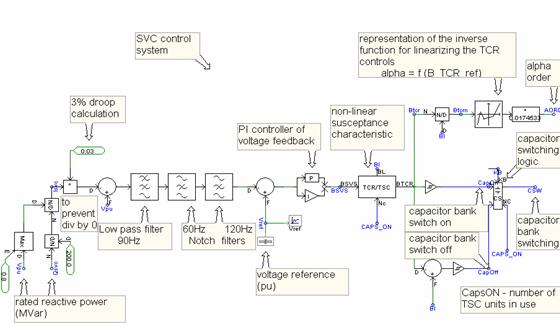
Figure 3. PSCAD representation of SVC control system [5]
The SVC can both absorb as well as supply reactive power at the bus it is connected to by control of the firing angle of the thyristor elements. By controlling the firing angle α of the thyristors (i.e., the angle with respect to the zero crossing of the phase voltage), the device is able to control the bus voltage magnitude. Changes in α results in changes on the current and hence, the amount of reactive power consumed by the inductor. When α = 90°, the inductor is fully activated but is deactivated when α = 180°. Actually, the basic control strategy is typically to keep the transmission bus voltage within certain narrow limits defined by a controller droop and the firing angle α limits (90° < α > 180°).
Studied System
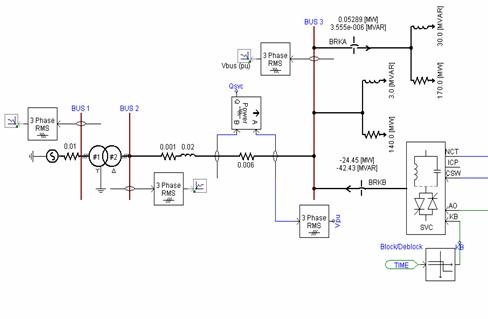
Figure 4. A 230kV power system with SVC connected at bus 3
Figure 4 shows a 230kV power network to which SVC is connected at bus 3. The power system comprises a generator generating 16kV which is stepped up by a transformer to 230kV. This voltage is transmitted via the transmission line to bus 3. The models of the generator and the SVC as well as the transformer parameters are the IEEE standard models of PSCAD/EMTDC [5].
Simulation and Results
The system under study is carried out in PSCAD/EMTDC when the generator is operating at its rated power level. The voltage at bus 3 having a load of 4MW and 3MVar is found approximately to be 230kV. But, when the load is increased to 150MW and 30MVar, the voltage dropped to 229.151kV. So, further increase in load resulted in the corresponding voltage drop at bus 3 as is shown in Table 1.
Table 1. Load variation with and without SVC
|
Loads |
Voltages in kV |
||
|
MW |
MVar |
Without SVC |
With SVC |
|
4 |
3 |
229.977 |
230.350 |
|
150 |
30 |
229.151 |
230.618 |
|
155 |
35 |
229.014 |
232.048 |
|
160 |
40 |
228.877 |
229.065 |
|
260 |
60 |
228.286 |
231.154 |
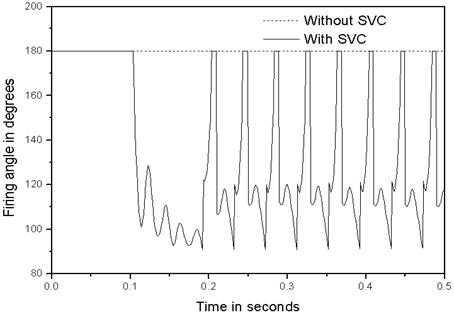
Figure 5. The firing angle at the same load with P = 4MW and Q = 3MVars
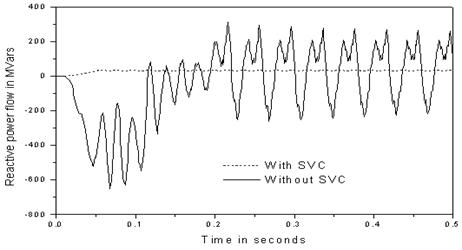
Figure 6. Reactive power flow at the load with P = 4MW and Q = 3MVars
However, with SVC connected to bus 3, the voltage required (230kV) is maintained even at the increase of load. It is observed that the voltage magnitude at bus 3 is maintained averagely to 230.65kV during load variation. When SVC is unconnected, the firing angle is 180° showing that the inductor is deactivated. However, the inductor is activated when SVC is connected and the firing angle is 116.9°, hence optimizing the reactive power and improving the voltage profile (See figures 5 – 6).
It should be noted here that changes in firing angle result on changes in the current, and hence the amount of reactive power consumed by the inductor. As the load increases, the firing angle decreases and hence more amount of reactive power is consumed by the inductor, and vice versa.
Conclusion
In this paper, the basic structure of an SVC operating under typical bus voltage control and its model are described. The model is based on representing the controller as variable impedance that changes with the firing angle of the Thyristor Controlled Reactor (TCR), which is used to control voltage in the system. Simulations carried out confirmed that Static Var Compensator could provide the fast acting voltage support necessary to prevent the possibility of voltage reduction and voltage collapse at the bus to which it is connected.
References
1. Cai L., Robust Co-ordinated Control of FACTS Devices in Large Power Systems a PhD thesis, University of Duisburg, Germany, published by Logos Verlag Berlin, 2004.
2. Acha E., Ambriz-Perez H., Fuerte-Esquivel, Advanced SVC Models for Newton-Raphson Load Flow and Newton Optimal Power Flow Studies, IEEE Transactions on Power Systems, 15(1), p.129-136, 2000.
3. Agelidis V. G. et all., Power Electronic Control in Electrical Systems, Newnes, 2002.
4. Hingorani N. G., Gyugyi L., Understanding FACTS concepts and Technology of flexible AC transmission systems, New York. IEEE Press, 2000.
5. Manitoba H. V. D. C. Research centre Inc., PSCAD/EMTDC manual version 3.0, 244 Cree Crescent, Winnipeg, Manitoba, Canada R3J 3W1.