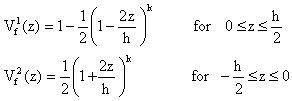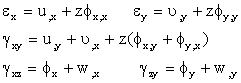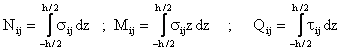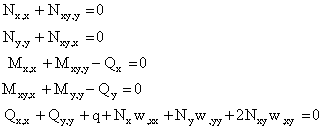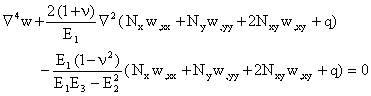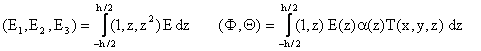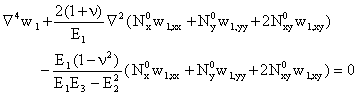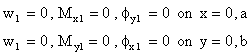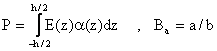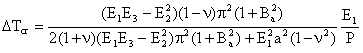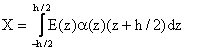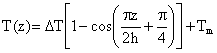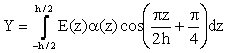Buckling Analysis of Functionally Graded Plates with Simply Supported Edges
Bouazza MOKHTAR1, 2, Tounsi ABEDLOUAHED2, Adda BEDIA EL ABBAS2, Megueni ABDELKADER3
1 Department of Civil Engineering, University of Béchar, Béchar 08000, Algeria.
2 Laboratory of Materials and Hydrology (LMH), University of Sidi Bel Abbès, Sidi Bel Abbès 2200, Algeria.
3 Department of Mechanical Engineering, University of Sidi Bel Abbès, Sidi Bel Abbès 2200, Algeria.
E-mail: bouazza_mokhtar@yahoo.fr
Abstract
Thermal buckling analyses of S-FGM are investigated by using first order shear deformation theory. Material properties are varied continuously in the thickness direction according to a sigmoid distribution. The thermal buckling behaviours under uniform, linear and sinusoidal temperature rise across the thickness are analyzed. In addition, the effects of temperature field, volume fraction distributions, and system geometric parameters are investigated. The results are compared with the results of the classic plate theory (CPT).
Keywords
Thermal buckling; Functionally graded material; First order shear deformation theory.
Introduction
Functionally graded materials (FGMs) have been designed and developed in many engineering parts that need to be super heat resistant, such as thermal barrier materials for Text for this section, aerospace structural applications and fusion reactors. In FGMs, material properties vary smoothly and continuously from one surface to the other, especially from metal to ceramic. From this smooth and continuous change in composition, FGMs can withstand extremely high temperature environments while maintain their structural integrity.
Nan et al. [1] directly address the constitutive relations of FGM and specifically, used an analytical approach to describe the uncoupled thermomechanical properties of metal/ceramic FGM. These novel materials were first introduced by a group of scientists in Sendai, Japan (Koizumi, [2]) and then rapidly developed by the scientists.
The nonlinear equilibrium equations and associated linear stability equations were expressed for bars, plates, and shells by Brush and Almroth [3]. The subject matter of this book is the buckling behavior of structural members subjected to mechanical loads. Subsequently, many researchers developed equilibrium and stability equations for plates and shells made of composite layered materials and used them to determine the buckling and vibration behaviour of structures. A review of recent developments in laminated composite plate buckling was carried out by Leissa [4]. Considerable research has focused on the buckling analysis of composite plates under mechanical and thermal loads based on the classical plate theory (Birman and Bert, [5]; Pandey and Sherbourne, [6] using the classical plate theory, which neglects the effects of transverse shear deformation, the calculations of the buckling loads are rather simple and generally may result in closed-form solutions.
In this study, Thermal buckling analyses of S-FGM are investigated by using first order shear deformation theory. Material properties are varied continuously in the thickness direction according to a sigmoid distribution. The thermal buckling behaviours under uniform, linear and sinusoidal temperature rise across the thickness are analyzed. In addition, the effects of temperature field, volume fraction distributions, and system geometric parameters are investigated. The results are compared with the results of the classic plate theory (CPT).
Theoretical Formulation
The functionally graded material (FGM) can be produced by continuously varying the constituents of multi-phase materials in a predetermined profile. The most distinct features of an FGM are the non-uniform microstructures with continuously graded properties. A FGM can be defined by the variation in the volume fractions. Most researchers use the power-law function, exponential function, or sigmoid function to describe the volume fractions. In order to avoid the stress concentrations appear in one of the interfaces (Lee and Erdogan [7]), the sigmoid function is used in this study.
Sigmoid FGM structures
In order to analyze sigmoid FGM structures as shown in Fig. 1, the sigmoid function (Lee and Erdogan [7], Bouazza et al [8]) can be employed in this study. The volume fraction using two power-law functions to ensure smooth distribution of stresses is defined.
|
|
(1) |
where h is the thickness of the plate and k
is the material parameter that dictates the material variation profile through
the thickness.
By using the rule of mixture, the material properties of the S-FGM can be calculated by:
|
|
(2) |
where E(z) denotes a generic material property such as modulus, Ec and Em indicate the property of the top and bottom faces of the structure, respectively.
Figure 1. Typical FGM square plate
Fig. 2 showed that the variation of volume fraction in Eq.(1) represents sigmoid distributions, and this FGM structure is thus called a sigmoid FGM structure (S-FGM structures). Consider an elastic rectangular plate. The local coordinates x and y define the mid-plane of the plate, whereas the z-axis originated at the middle surface of the plate is in the thickness direction. The material properties, Young's modulus, on the upper and lower surfaces are different but are pre-assigned according to the performance demands. However the Young's modulus of the plates and vary continuously only in the thickness direction (z-axis) i.e., E=E(z). It is called functionally graded material (FGM) plates. There have been numerous works on studying the response of FG plates made of isotropic elastic constituents with the homogenized material also modelled as isotropic elastic, the only other study on FG anisotropic plate [9] has assumed that all elastic constants vary exponentially through the plate thickness at the same rate. It is highly unlikely that elastic modulus of a FG anisotropic plate will exhibit this property.
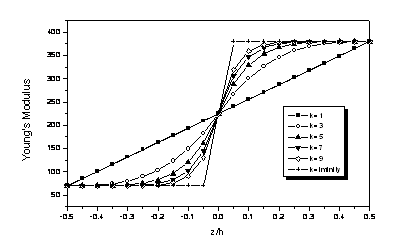
Figure 2. Young’s modulus variation associated with different exponent indexes for a S-FGM plate
Stability equations
Assume that u,v,w denote the displacements of the neutral plane of the plate in x, y, z directions respectively; εx, εy denote the rotations of the normal to the plate mid-plane. According to the first order shear deformation theory, the strains of the plate can be expressed:
|
|
(3) |
The forces and moments per unit length of the plate expressed in terms of the stress components through the thickness are:
|
|
(4) |
The nonlinear equations of equilibrium according to Von Karman’s theory are given by:
|
|
(5) |
Using Eqs.(2) (3) and (4), and assuming that the temperature variation is either linear with respect to x- and y-directions, or constant, the equilibrium Eq. (5) may be reduced to a set of two equations as:
|
|
(6) |
where
|
|
(7) |
To establish the stability equations, the critical equilibrium method is used. Assuming that the state of stable equilibrium of a general plate under thermal load may be designated by w0. The displacement of the neighbouring state is w0+w1, where w1 is an arbitrarily small increment of displacement. Substituting w0+w1 into Eq.(6) and subtracting the original equation, results in the following stability equation:
|
|
(8) |
where, ![]() refer to the pre-buckling
force resultants
refer to the pre-buckling
force resultants
To determine the buckling temperature difference ΔTcr, the pre-buckling thermal forces should be found firstly. Solving the membrane form of equilibrium equations, gives the pre-buckling force resultants:
|
|
(9) |
Substituting Eq(9) into Eq. (8), one obtains:
|
|
(10) |
The simply supported boundary condition is defined as:
|
|
(11) |
The following approximate solution is seen to satisfy both the governing equation and the boundary conditions:
|
|
(12) |
where m, n are number of half waves in the x and y directions, respectively, and c is a constant coefficient.
Buckling Analysis
In this section, the thermal buckling behaviours of fully simply supported rectangular metal – ceramic plates under thermal environment are analyzed. The thermal load is assumed to be uniform, linear and sinusoidal temperature rise through the thickness direction. The reference temperature is assumed to be 5°C. The effects of volume fraction index and geometric parameter a/h are investigated in each case.
Table 1. Material properties of metal and ceramic [10, 11]
|
Material |
Property |
||||
|
E (GPa) |
ρ(kg/m3) |
ν |
α (1/°C) |
k(W/mk) |
|
|
Aluminum Alumina |
70 380 |
2707 3800 |
0.3 0.3 |
23e-6 7.4e-6 |
204 10.4 |
Uniform temperature rises
Substituting Eq. (12)
into Eq. (10), and substituting for the thermal parameter ![]() from Eq. (7), yields:
from Eq. (7), yields:
|
|
(13) |
where:
|
|
(14) |
The critical temperature difference is obtained for the values of m=n=1.
|
|
(15) |
The variation of the critical temperature change ΔTcr of metal -ceramic S-FGM plates under uniform temperature rise according to a/h and plate aspect ratio a/b is presented in Fig. 3. The cases of a/b = 1, 0.75, 0.5and 0.25 are for the graded plates with two constituent materials. In this figure, the as aspect ratio a/b is decreased, the critical temperature change decreases. However, the critical temperature change decreases rapidly, when the geometric parameter a/h is increased. Thus when the plates are thicker, the critical temperature change becomes higher.
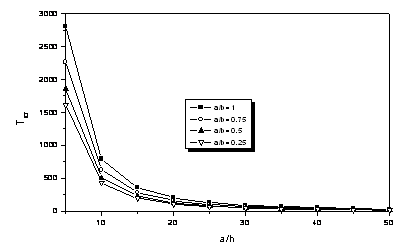
Figure 3. Critical temperature change with respect to aspect ratio and a/h under uniform temperature rise
Linear Temperature Rise
The temperature field under linear temperature rise through the thickness is assumed as:
|
|
(16) |
where z is the coordinate variable in the thickness direction which measured from the middle plane of the plate.
Tm is the ceramic temperature and DT is the temperature difference between metal surface and ceramic surface, i.e., DT = Tc - Tm. For this loading case, the thermal parameter Φ can be expressed as:
|
|
(17) |
where:
|
|
(18) |
From Eq.(17) one has:
|
|
(19) |
By solving Eq.(19), the critical temperature gradient DTcr can be obtained. Fig. 4 gives the variation of the critical temperature gradient DTcr of fully clamped Aluminum–Alumina FGM plates under linear temperature rise. The responses are very similar comparing to those under uniform temperature rise; however, the critical temperature gradient under linear temperature rise is higher than that under uniform temperature rise.
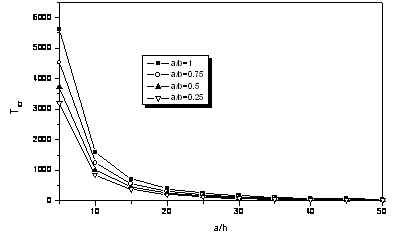
Figure 4. Critical temperature gradient with respect to aspect ratio and a/h under linear temperature rise
Sinusoidal temperature rise
The temperature field under sinusoidal temperature rise across the thickness is assumed as:
|
|
(20) |
where T(z) is the temperature gradient. From Eq(20) and (7) the expression become as follows:
|
|
(21) |
where:
|
|
(22) |
From Eq.(21):
|
|
(23) |
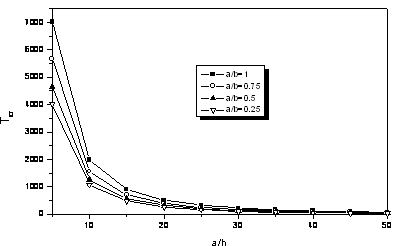
Figure 5.Critical temperature gradient with respect to aspect ratio and a/h under sinusoidal temperature rise
By solving Eq.(23), the critical temperature gradient ΔTcr can be obtained. The critical temperature gradient with respect to aspect ratio a/b and a/h is presented in Fig. 5. The responses are very similar comparing to previous results, but the critical temperature gradient of sinusoidal temperature rise is the highest in three cases. The critical temperature gradient increases as aspect ratio a/b is increased. When a/h is increased, the critical temperature gradient decreases, rapidly. From the results, one can find that as the plates are thicker, the critical temperature gradient becomes higher.

Figure.6. Comparison between temperature graphs vs. ratio b/h based on first order shear deformation theory, classic plate theory in the case of uniform temperature rise with simply supported edge

Figure.7. Comparison between temperature graphs vs. ratio b/h based on first order shear deformation theory, classic plate theory in the case of linear temperature rise with simply supported edge.

Figure 8. Comparison between temperature graphs vs. ratio b/h based on first order shear deformation theory, classic plate theory in the case of sinusoidal temperature rise with simply supported edge
In Figures 6-8 the graphs of results of thermal buckling analysis for the S-FGM based on the FSDT compared to CPT are presented. This figure shows that the buckling temperature increases when the ratio b/h reduces. Also, based on the figure, the results obtained by first order shear deformation theory coincide well with the results of classic plate theory, except for very low values of b/h. This is well explained by the large plate aspect ratio b/h=20, 30, 40, 50,60,70,80, 90,100 or the small plate thickness h.
Conclusions
Thermal buckling of rectangular Aluminum–Alumina plates under thermal environment is investigated by using first order shear deformation theory. The thermal load is assumed to be uniform, linear and sinusoidal temperature rise through the thickness direction. In thermal buckling analysis, as geometric parameter a/h is increased, the critical temperature gradient decreases rapidly. When plate aspect ratio a/b is decreased, the critical temperature reduces as the plate becomes thinner. The critical temperature under sinusoidal temperature rise has the highest value in three cases, and that under linear temperature rise is higher than that under uniform temperature rise.
References
1. Nan C. W., Yuan R. Z., Zhang L. M. , The physics of metal/ceramic functionally gradient materials, Ceramic. Trans. Funct. Gradient Mater. 1993, 34, p. 75-82.
2. Koizumi M., FGM activities in Japan, Composites Part B 1997, 28(1–2), p. 1-40.
3. Brush D. O., Almroth B. O., Buckling of Bars, Plates and Shells, McGraw-Hill, New York, 1975.
4. Leissa A. W. Review of recent developments in laminated composite plate buckling analysis, Composite Mat. Tech. 1992, 45, p. 1-7.
5. Birman V., Bert C. W, Buckling of composite plate and shells subject to elevated temperature, Trans. ASME J. Appl. 1993, 60, p. 514-519.
6. Pandey M. D., Sherbourne A. N,. Buckling of anisotropic composite plates under stress gradient, J. Engrg. Mech. 1991, 117(2), p. 260-275.
7. Lee Y. D., Erdogan F., Residual/thermal stress in FGM and laminated thermal barrier coatings, Int J Fracture 1995, 69, p. 145-165.
8. Bouazza M., Tounsi A., Adda-Bedia E. A., Megueni A. Thermal buckling of sigmoid functionally graded plates using first order shear deformation theory, MAMERN09: 3rd International Conference on Approximation Methods and Numerical Modeling in Environment and Natural Resources Pau (France), June 8-11, 2009.
9. Pan E., Exact solution for functionally graded anisotropic composite laminates. J Compos Mater 2003, 37, p. 1903-20.
10. Javaheri R., Eslami M. R., Buckling of functionally graded plates under in-plane compressive loading, ZAMM Z Angew Math Mech 2002, 82(4), p. 277-83.
11. Javaheri R., Eslami M. R., Thermal buckling of functionally graded plates, AIAA, 2002, 40(1), p. 162-9.