Modelling and Estimation of Hammerstein System with Preload Nonlinearity
Khaled ELLEUCH1 and Abdessattar CHAARI2
UCA Unit of Automatic Control National Engineering School of Sfax, B. P: 1173, 3038 Sfax, Tunisia.
E-mails: 1ked_elleuch@yahoo.fr, 2abdessattar2004@yahoo.fr:
Abstract
This paper deals with modelling and parameter identification of nonlinear systems described by Hammerstein model having asymmetric static nonlinearities known as preload nonlinearity characteristic. The simultaneous use of both an easy decomposition technique and the generalized orthonormal bases leads to a particular form of Hammerstein model containing a minimal parameters number. The employ of orthonormal bases for the description of the linear dynamic block conducts to a linear regressor model, so that least squares techniques can be used for the parameter estimation. Singular Values Decomposition (SVD) technique has been applied to separate the coupled parameters. To demonstrate the feasibility of the identification method, an illustrative example is included.
Keywords
Identification; Hammerstein model; preload nonlinearity; generalised orthonormal basis; Singular Values Decomposition.
Introduction
In the last decades, a considerable effort of research has been deployed to modelling, identification and control of nonlinear systems using nonlinear models such block-oriented nonlinear models. Among these models, we can cite particularly Hammerstein model, Wiener model and Hammerstein-Wiener model. This category of nonlinear dynamic systems is studied by many researchers in automatic control [1-5].
Recursive identification methods, that are well adapted to a great number of real time applications, are extensively developed. In addition, they can be easily combined with on-line control strategies to produce adaptive control algorithms [6]. Some of these methods were applied to the nonlinear systems of Hammerstein type with different forms of discontinuous piecewise-linear nonlinearity [1, 7]. In these approaches, a parameter redundancy was considered and leads, therefore, to a significant increase of the number of estimated parameters. Other forms of Hammerstein models based on the key-term separation principle are described in the literature. In this case, the static nonlinearity is represented by piecewise nonlinearities [8-11]. Such models are linear in parameters and the recursive least square algorithm can be applied [9]. Other method of Hammerstein model parameter identification, based on a key term separation principle and a substitution providing a nonlinear model which represents a MISO system [8], is suggested. The considered Hammerstein models contain an internal variable not available to the measure thus it is necessary to build the observations vector what requires the manipulation of a great number of iterations ensuring the least squares algorithm convergence [1, 7, 8, 9].
In this paper, we propose a new approach to the parameter identification of nonlinear dynamic systems based on Hammerstein models where the linear dynamic block is described by generalised orthonormal basis and the static nonlinearity is formulated by a preload nonlinearity characteristic. To estimate the parameters, a proper switching function is incorporated. Thereafter, the recursive least square algorithm will be applied and the SVD will be used to obtain the optimal estimates of the parameter matrices.
Description of Hammerstein models
Hammerstein model is one of the most easy and known of the family of blocks oriented nonlinear systems [12]. The Hammerstein model is given by the cascade connection of a static nonlinearity block N(.) followed by a linear dynamic system defined by a transfer function H(q) shown in Figure 1. In this paper, a special form of mathematical Hammerstein model containing internal variable and proper switching function is developed where the linear dynamic block is described by generalized orthonormal basis and the static nonlinearity is represented by a piecewise linear characteristic such us preload nonlinearity function N(.).
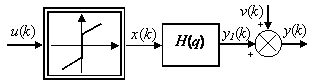
Figure 1. Hammerstein model
where: u(k) : model input; y1(k): model output without noise; y(k) : noisy model output; x(k) : internal variable which represents the output of nonlinear block, not available to the measure;
v(k) : noise of measure in the output.
Description of the static nonlinear block
The static nonlinear block is described by a preload nonlinearity characteristic. In this case, the slopes S1, S2 and the values of crossing C1, C2, are parameters to be estimated. These parameters can be positive or negative, Figure 2.
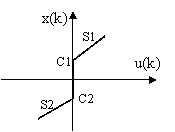
Figure 2. Preload nonlinearity
The output of the nonlinear block x(k) depends on the position of the input signal u(k) in regard with the points of discontinuities zero. It is written in the following way:
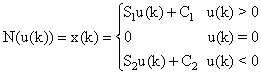 (1)
(1)
We define a switching function, described by the following equation:
![]() (2)
(2)
then the static nonlinearity output x(k) can be written as:
![]() (3)
(3)
Description of the dynamic linear block
The dynamic linear block is represented by a discrete transfer function H(q) given by:
![]() (4)
(4)
where p designates the number of poles and ![]() represents the generalized orthonormal basis
which are described by the following relationships:
represents the generalized orthonormal basis
which are described by the following relationships:
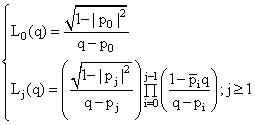 (5)
(5)
where ![]() is
the pole number i and
is
the pole number i and ![]() represents its conjugate.
represents its conjugate.
Then, the system output can be defined by the following equation:
![]() (6)
(6)
In a matrix form, we can write the system output equation as follows:
![]() (7)
(7)
where ![]() is the parameters
vector and
is the parameters
vector and ![]() is the observations vector,
they are respectively, given by:
is the observations vector,
they are respectively, given by:
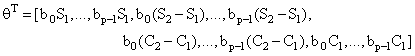 (8)
(8)
and
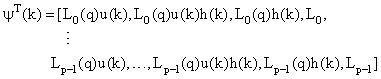 (9)
(9)
Estimation algorithm of the Hammerstein model
In a first step, we estimate the parameters of vector ![]() using the recursive least squares algorithm by
minimizing the quadratic criterion on the prediction error as follows:
using the recursive least squares algorithm by
minimizing the quadratic criterion on the prediction error as follows:
![]() (10)
(10)
The RLS algorithm can be formulated by solving the quadratic criterion:
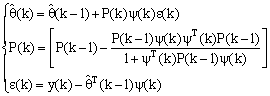 (11)
(11)
where ![]() is the
prediction error, and
is the
prediction error, and ![]() designates
the adaptation matrix.
designates
the adaptation matrix.
A second step is devoted to estimate separately the parameters bi, Si and Ci parameters. For this purpose, we use the SVD decomposition [13] by assuming:
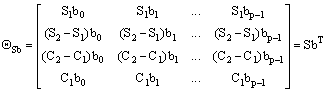 (12)
(12)
with: ![]() and
and ![]()
The estimate ![]() of matrix
of matrix ![]() can
be obtained by the RLS algorithm which allows to compute
can
be obtained by the RLS algorithm which allows to compute ![]() and the estimates
and the estimates ![]() and
and ![]() . These estimates will be obtained by minimizing the following
criterion:
. These estimates will be obtained by minimizing the following
criterion:
![]() (13)
(13)
The previous equation is solved using the SVD decomposition of ![]() such as:
such as:
![]() (14)
(14)
where Nk is a diagonal matrix containing the k non-zero
singular values ![]() of
of ![]() and the matrixes
and the matrixes ![]() and
and ![]() contain only the first k columns of the unitary matrixes U
and V provided by the full SVD of
contain only the first k columns of the unitary matrixes U
and V provided by the full SVD of ![]() described by the following relationship.
described by the following relationship.
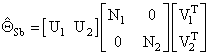 (15)
(15)
with dim (U1) =dim (S) et dim (V1) =dim (b)
and the N1 block is, in fact, the first singular value ![]() of
of ![]() . It results that the estimates can be written as:
. It results that the estimates can be written as:
![]() (16)
(16)
![]() (17)
(17)
Simulation Results
The proposed method for the parameter estimation of nonlinear dynamic systems with discontinuous nonlinearities using the Hammerstein model was implemented and tested by means of MATLAB packages. The estimation of the model parameters (those of linear and nonlinear blocks) were carried out on the basis of input and output records. To illustrate the feasibility of the proposed identification method, the following example shows the parameters estimation process for the linear dynamic block, which is given by the following recursive equation:
![]() (18)
(18)
The discontinuous nonlinearity is described by the following parameters:
![]() ,
, ![]() ,
, ![]() ,
, ![]()
The identification was carried out with 1000 samples of uniformly distributed random inputs and simulated outputs. The output noise was generated as a zero mean white noise and the Signal to Noise Ratio (the square root of the ratio of output and noise variances) was (SNR =10, 50 and 100).
The evolution curves, for the estimate of coupled parameters with a value of SNR equal to 10, are given in Figure 3.
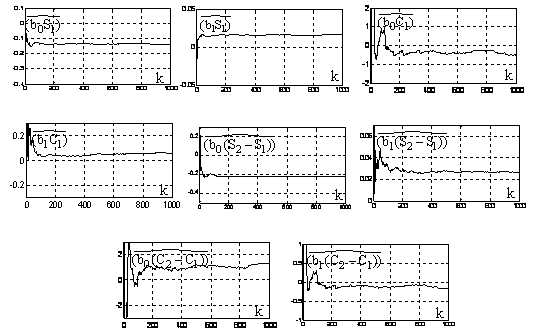
Figure 3. Curves for the estimate of coupled parameters.
We give, in Tables 1 and 2, the estimate values of coupled and separate parameters.
Table 1. Estimate values of coupled parameters
|
SNR |
|
|
|
|
|
|
|
|
|
10 |
-0.1361 |
0.0163 |
-0.4663 |
0.0559 |
-0.2248 |
0.0268 |
1.2771 |
-0.1541 |
|
50 |
-0.1352 |
0.0164 |
-0.4507 |
0.0545 |
-0.2251 |
0.0272 |
1.2614 |
-0.1525 |
|
100 |
-0.1351 |
0.0162 |
-0.4501 |
0.0540 |
-0.2249 |
0.0270 |
1.2605 |
-0.1512 |
Table 2. Estimate values of separate parameters
|
SNR |
|
|
|
|
|
|
|
10 |
-0.3003 |
0.0362 |
0.4517 |
1.1962 |
1.5485 |
-2.7100 |
|
50 |
-0.3002 |
0.0363 |
0.4510 |
1.2003 |
1.5010 |
-2.7005 |
|
100 |
-0.3001 |
0.0360 |
0.4507 |
1.1998 |
1.5005 |
-2.7001 |
Discussion
The previous curves show a good convergence of the algorithm. Indeed, the estimate parameters fluctuations appearing in the early samples are not severe. The statistical average, for the estimate of coupled and separate parameters of the last two hundred samples with various values of SNR (10, 50 and 100), is respectively given in previous Table1 and Table 2.
The estimation results, for this kind of model, have proved the efficiency of this method for an acceptable value of SNR. Indeed, for the value of SNR equal to 10, the estimate parameters of the static nonlinear block are closed to the exact values. If the values of SNR increase, the estimates converge more towards the exact values.
Conclusions
In this paper, a new approach, in modelling and parameters identification of Hammerstein models with preload nonlinear characteristic and containing an internal variable and proper switching function, has been developed. The main contribution, in this work, has been dedicated to a new description of Hammerstein model by the introduction of a proper switching function and the use of the generalised orthonormal basis. This parameterization of the considered Hammerstein model leads to a linear regressed form so that least square techniques have been successfully used to estimate an oversized parameter matrix. Then, by recurring to SVD, optimal estimates of the parameter matrices characterizing the linear and nonlinear parts have been determined. The included example of the identification process has shown the feasibility and good convergence properties of the proposed technique.
References
1. Bai E.W., Identification of linear systems with hard input nonlinearities of known structure, Automatica 2002, 38(5), p. 853-860.
2. Kung M. C., Womack B. F., Discrete time adaptive control of linear systems with preload nonlinearity, Automatica 1984, 20, p. 477-479.
3. Tao G., Tian, M., Discrete-time adaptive control of systems with multisegment piecewise-linear nonlinearities, IEEE Trans. Autom. Control 1998, 43(5), p. 719-723.
4. Van Pelt T. H., Bernstein D. S., Nonlinear system identification using Hammerstein and nonlinear feedback models with piecewice linear static maps, Int. J. Control 2001, 74(18), p. 1807-1823.
5. Vörös J., Parameter Identification of Discontinuous Hammerstein Systems, Automatica 1997, 33(6), p. 1141-1146.
6. Chidambaram M., Computer Control of Processes, New York: CRC, 2001.
7. Kung M. C., Womack B. F., Discrete time adaptive control of linear dynamic systems with a two-segment piecewise-linear asymmetric nonlinearity, IEEE Trans. Autom. Control, 1984, AC-29(2), p. 170-172.
8. Guo F., Bretthauer G., Identification of MISO Wiener and Hammerstein systems, Proceedings of the 7th European Control Conference, TEE, University of Cambridge, UK, September, 2003.
9. Vörös J., Iterative algorithm for parameter identification of Hammerstein systems with two-segment nonlinearities, IEEE Transactions on Automatic Control, 1999, (44), p. 2145-2149.
10. Vörös J., Modelling and parameter identification of systems with multi segment piecewise-linear characteristics, IEEE Transactions on Automatic Control, 2002, AC 47(1), p. 184-188.
11. Vörös J., Identification of Hammerstein systems with time-varying piecewise-linear characteristics nonlinearities, Journal of Electrical Engineering, 2005, 57(1), p. 42-46.
12. Billings S., Fakhouri S., Identification of systems containing linear dynamic and static nonlinear elements, Automatica 1982, p. 15-26.
13. Golub G., Van Loan C., Matrix Computations, second ed., The Johns Hopkins University Press, Baltimore and London, 1989.