Fully Implicit Four Point Block Backward Difference Formulae for Solving First Order Initial Value Problems
Umaru MOHAMMED and Yusuph Amuda YAHAYA
Maths/Computer Science Department, Federal University of Technology, Minna, Nigeria.
E-mails: digitalumar@yahoo.com, yusuphyahaya@yahoo.com
(* Corresponding author)
Abstract
The four steps Backward Differentiation Formulae (BDF) were reformulated for applications in the continuous form. The process produces some schemes which are combined in order to form an accurate and efficient block method for parallel or sequential solution of ordinary differential equations (ODE’s). The suggested approach eliminates requirement for a starting value and its speed proved to be up when computations with the Block Discrete schemes were used.
Keywords
Backward Differentiation Formulae (BDF); Block Method; Parallelism; Sequential.
Introduction
Consider the initial value problems for the system/scalar ordinary differential equations (ODEs).
![]() (1)
(1)
In the literature, conventional linear multistep methods including hybrid ones have been made continuous through the idea of multistep collocation (MC) [1-5]. The Continuous Multistep Method (CMM) method produces piece-wise polynomial solutions over K-steps [Xn, Xn+k] for the first order systems/scalar ODEs. Of note, is that the implicit [CMM] interpolant (12) is not to be directly use as the numerical integrator, but the resulting discrete multistep Schemes which is derived from it, which will now be self- starting and can be applied for parallel or sequential solutions of both the initial and boundary value problems.
In this paper is part of research effort to reformulate for efficient and accurate use, the linear multistep methods and four step block differentiation formulae (BDF) is considered here.
Derivation of proposed approximate solution
Def 1.1 A-Stable (Dahlqquist [6])
A numerical method is said to be A-stable if its region
of absolute stability contains, the whole of the left-hand half-plane![]()
Definition 1.2:A(α) stable (Widluid [7])
A numerical method is said to be ![]() , if its region of absolute stability
contains the infinite wedge
, if its region of absolute stability
contains the infinite wedge![]() ; it is
said to be A (0) - stable if it is
; it is
said to be A (0) - stable if it is ![]() stable for
some (sufficiently small)
stable for
some (sufficiently small) ![]()
Definition 1.3
A block method is zero-stable provided the roof ![]() s of the first characteristics
polynomial
s of the first characteristics
polynomial ![]() specified as
specified as ![]() satisfies
satisfies ![]() and
for those roots with
and
for those roots with ![]() the multiplicity
must not exceed two. The principal root of
the multiplicity
must not exceed two. The principal root of ![]() is
denoted by
is
denoted by ![]()
General multistep collocation (MC) Linked to Continuous Multistep Method (CMM)
Let us first give a general description for the method of multistep collocation (MC) and its link to Continuous Multistep Method (CMM) for (1). In the equation (1), f is given and y is sought as
![]() (2)
(2)
where
![]()
xn ≤x≤xn+k, where n = 0, k, … n-k, T = “Transpose of”
Equation (2) can be re-written as
![]() (3)
(3)
The unknown coefficients a1, a2, … ap are determined using respectively the r (0<r<=k) interpolation conditions and the s>0 distinct collocation conditions, p=r+s as follows
![]()
![]() (4)
(4)
This is a system of p linear equations from which we can compute values for the unknown coefficients provided (4) is assumed non-singular, for the distinct points xi and ci the non-singular system is guaranteed (see proof in Yusuph and Onumanyi 2002). We can write (4) as a single set of linear equations of the form
![]()
![]() (5)
(5)
Where![]() (6)
(6)
Substituting the vector a, given by (5) and F by (6) into (3) gives
![]() (7)
(7)
Equation (7) is the continuous MC Interpolant CT known explicitly in the form
 (8)
(8)
![]()
Or
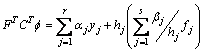 (9)
(9)
Where from (8)
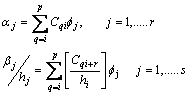 (10)
(10)
Therefore,
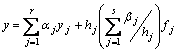 (11)
(11)
where ![]() are given by (10). Hence (11) with (10) is the CMM interpolant with
uniform or variable step-size.
are given by (10). Hence (11) with (10) is the CMM interpolant with
uniform or variable step-size.
We propose an approximate solution to (1) in the form
![]() (12)
(12)
with m = 0, t = 4 and p = m+t -1 also ![]() are the parameters to
be determined where p is the degree of the polynomial interpolant of our choice.
Specifically, we interpolate equation (12) at
are the parameters to
be determined where p is the degree of the polynomial interpolant of our choice.
Specifically, we interpolate equation (12) at ![]() using the method
described in this paper; we obtain a continuous form for the solution
using the method
described in this paper; we obtain a continuous form for the solution ![]() from the system of the equation in the
matrix below.
from the system of the equation in the
matrix below.
The general form of the new method is expressed a
![]()
The matrix D of the new method expressed as:
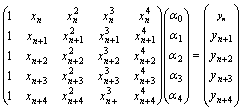
Matrix D in the equation above, which when solved either by matrix inversion techniques or Gaussian elimination method to obtain the values of the parameters j = 0,1,(m+t-1) and then substituting them into equation (12) give a scheme expressed in the form.
![]()
If we now let k=4, after some manipulation we obtain a continuous form of solution.
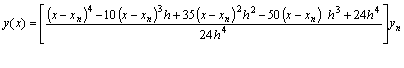
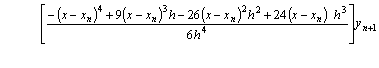
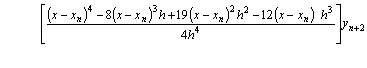
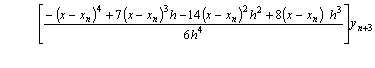
![]() (13)
(13)
Differentiating equation (13) once, yielded

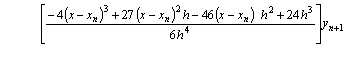
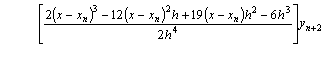
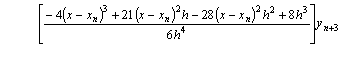
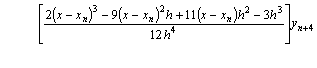 (14)
(14)
Evaluating (14) at x=xn+4, we obtain
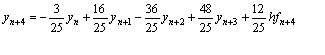 (15)
(15)
This is the existing method of (BDF) (see Lambert [8], [9]) of order four (4) with error constant E = 12h5y5/125.
Evaluating equation (14) at point x = xn+3, x = xn+2, and x = xn+1we obtain respectively
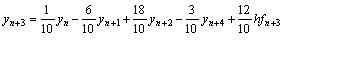
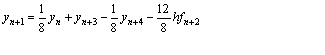
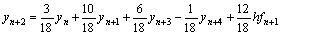 (16)
(16)
Equation (15) and (16) constitute the member of a
zero-stable block integrators of order (4,4,4,4)T with ![]() the
application of the block integrators with n=0 give the accurate values of
the
application of the block integrators with n=0 give the accurate values of![]() along with
along with ![]() as shown in
table (1-2 )
as shown in
table (1-2 )
To start the IVP integration on the sub-interval [x0,
x4]. We combine (15) and (16), when n=0 i.e the 1-block 4 point method
as given in equation (17) produces its unknown simultaneously without recourse
to any starting method(predictor) to generate![]() before computing
before computing ![]() using
equation (15) in the main method (see Lambert [6,7] . Hence this is an improvement
over this reported works. Though, this does not becloud the contribution of
these authors.
using
equation (15) in the main method (see Lambert [6,7] . Hence this is an improvement
over this reported works. Though, this does not becloud the contribution of
these authors.
Results and Discussion
Recall, that, it is a desirable property for a numerical integrator to produce solution that behave similar to the theoretical solution to a problem at all times. Thus several definitions, which call for the method to possess some “adequate” region of absolute stability, can be found in several literatures. See Lambert [8], Fatunla [10,11]etc. following Funtula [10], the four integrator proposed in this report in equations (15) and (16) are put in the matrix-equation form and for easy analysis the result was normalized to obtain;
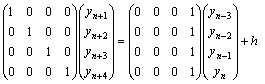
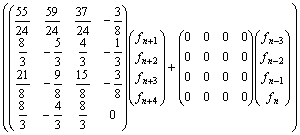 (17)
(17)
The first characteristic polynomial of the proposed
1-block 4 step method is ![]()
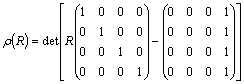 (18)
(18)
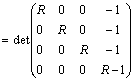
![]()
![]() This implies, R1 = R2
= R3 = 0, R4 = 1
This implies, R1 = R2
= R3 = 0, R4 = 1
From definition (1.3) and equation (18), the 1 block 4-point is zero stable and is also consistent as its order (4,4,4,4) T >1, thus, it is convergent, following Henrici [12]
Remarks 4.1
Using the matlab package, we were able to plot the stability region of the proposed block method. This is done by reformulating a block method as general linear method to obtain the values of the matrices A,B,U,V which are then substituted into stability matrix and stability function. Then the utilized maple package yield the stability polynomial of the block method. Using a matlab program we plot the absolute stability region of proposed four step block backward differentiation formulae (BDF).
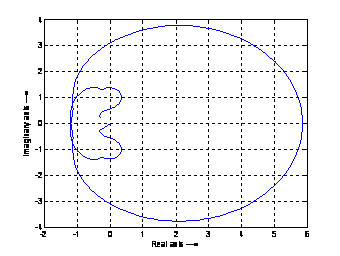
Figure 1. Region of Absolute Stability
From
definition (1.2) and figure (1) above the proposed four point block (BDF)
method (17) is ![]() stable.
stable.
Numerical Experiment
To illustrate the potentials of the new formulas constructed in this paper, we will compare their performance on the same problem when (BDF) scheme is used singly. (Note that is not self starting) we shall use other (BDF) for k=1, 2, 3 to get it started (ie to obtain y1, y2, y3). While the proposed four points block (BDF) type method is self starting on its own.
Consider the initial value problem

Table 1. Proposed (BDF) block method
|
N |
X |
Approx value |
Exact value |
Error |
|
0 |
1 |
1.0000000000 |
1.0000000000 |
0 |
|
1 |
0.1 |
0.9048399472 |
0.9048374180 |
2.5292000001E-06 |
|
2 |
0.2 |
0.8187328468 |
0.8187307531 |
2.0937000000E-06 |
|
3 |
0.3 |
0.7408202286 |
0.7408182207 |
2.0078999999E-06 |
|
4 |
0.4 |
0.6703216658 |
0.6703200460 |
1.6198000000E-06 |
|
5 |
0.5 |
0.6065338205 |
0.6065306597 |
3.1608000001E-06 |
|
6 |
0.6 |
0.5488143655 |
0.5488116361 |
2.7293999999E-06 |
|
7 |
0.7 |
0.4965878495 |
0.4965853038 |
2.5457000000E-06 |
|
8 |
0.8 |
0.4493311354 |
0.4493289641 |
2.1713000000E-06 |
|
9 |
0.9 |
0.4065727605 |
0.4065696597 |
3.1008000000E-06 |
|
10 |
1.0 |
0.3678821594 |
0.3678794412 |
2.7182000000E-06 |
Table 2. k=4 (BDF) schemes only, using a starting value (y1, y2, y3) computed from other(BDF)for k=1, 2,3
|
N |
X |
Approx value |
Exact value |
Error |
|
0 |
1 |
1.0000000000 |
1.0000000000 |
0 |
|
1 |
0.1 |
0.9090909091 |
0.9048374180 |
4.2534911000E-03 |
|
2 |
0.2 |
0.8238636362 |
0.8187307531 |
5.1328831000E-03 |
|
3 |
0.3 |
0.7454937301 |
0.7408182207 |
4.6755094000E-03 |
|
4 |
0.4 |
0.6744298736 |
0.6703200460 |
4.1098276000E-03 |
|
5 |
0.5 |
0.6102826374 |
0.6065306597 |
3.7519777000E-03 |
|
6 |
0.6 |
0.5523053404 |
0.5488116361 |
3.4937043000E-03 |
|
7 |
0.7 |
0.4908308572 |
0.4965853038 |
5.7544466000E-03 |
|
8 |
0.8 |
0.4276690805 |
0.4493289641 |
2.1659883600E-02 |
|
9 |
0.9 |
0.3691527030 |
0.4065696597 |
3.7416956700E-02 |
|
10 |
1.0 |
0.3185377346 |
0.3678794412 |
4.9341706600E-02 |
In this paper one block method was proposed and to test for their efficiency. One test example was solved with a derived block method. Their results were presented in tables 4.1-4.2. It will be observed that four step block backward differentiation method gives better result than when four step BDF scheme is using single. As it gives the smallest error.
However, the block method (BM) produces very accurate result, when compared with exact solution.
Conclusion
We have converted to continuous form the well known BDF. The continuous formulae are immediately employed as block method for direct solution of four point ivps. The direct solutions are in discrete form which can be substitution into the continuous formula for dense output. The proposed method is self starting, convergent and A(α) stable as shown by the plotted region of absolute stability. The method has been tested on simple ODEs and shown to perform satisfactory, without recourse to any other method to provide a starting value.
References
1. Lie I., Norset S.P., Supper Convergence for Multistep Collocation, Math. Comp, 1989, 52, p. 65- 79.
2. Onumanyi P., Awoyemi D.O., Jator S.N and Sirisena U.W., New linear Multistep with Continuous Coefficients for First Order Initial Value Problems, J. Nig. Math. Soc., 1994, 13, p. 37- 51
3. Onumanyi P., Jator S.N and Sirisena U.W., Continous Finite difference Approximate for Solving Differential Equations, J. Nig. Math. Soc., 1999, 1, p. 15- 27
4. Yusuph Y.A. and Onumayi p., New Multiple FDMS through multi step collocation for y” = f(x, y), Abacus, 2002, 29(2), p. 92- 100
5. Yahaya Y.A., some theory and application of continous linear multi-step methods for ordinary differential equation, ph.D thesis (unpublished) university of jos, Nigeria,2004
6. Dahlquist, G., A special stability problem for linear multi step methods , BIT 3, 1963, p. 27-43
7. Widlund, O. B., note on unconditionally stable linear multistep methods BIT 7, 1967, p. 65-70.
8. Lambert J.D., Computational Methods in Ordinary Differential Equations, New York, John Wiley and Sons, 1973.
9. Lambert J.D., Numerical Method for Ordinary Systems, New York, John Wiley and Sons, 1991.
10. Fatunla S.O., Parallel methods for second order ODE`s computational ordinary differential equations, proceeding of computer conference (eds),1992, p. 87-99.
11. Fatunla S.O., Higher order parallel methods for second order ode`s, proceeding of fifth international conference on scientific computing (eds fatunla), 1994, p. 61-67.
12. Henrici P., Discrete variable methods for ode`s, New York USA, John Wiley and sons, 1962.