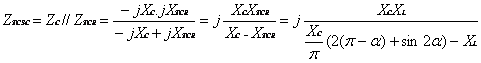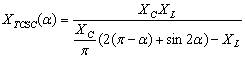Impact of Thyristors Controlled Series Capacitor Devices and Optimal Power Flow on Power Systems
Fatiha LAKDJA1, Fatima Zohra GHERBI2*
1,2 Electrical Engineering Department. Intelligent Control and Electrical Power System Laboratory (ICEPS), Djillali Liabes University, Sidi-Bel-Abbes, 22000, Algeria.
E-mail: flakdja@yahoo.fr, fz_gherbi@yahoo.fr
(* Phone/Fax: 213 48 54 41 00)
Abstract
This paper presents an algorithm, for solving the Optimal Power Flow problem with flexible AC transmission systems (FACTS). The type of FACTS devices is used: thyristor-controlled series capacitor (TCSC). A method to determine the optimal location of thyristor controlled series compensators has been suggested. The proposed approaches have been implemented on an adapted IEEE 26 bus system. The simulation results are discussed to show the performance of the proposed algorithm and our “FACTS programmer “simulator technique, which are compared with TCSC and without TCSC.
Keywords
Optimization problem; Power Flow; Optimal Power Flow; FACTS devices; TCSC.
Introduction
In a competitive electricity market, congestion occurs when the transmission network is unable to accommodate all of the desired transactions due to a violation of system operating limits. Congestion does occur in both electrically bundled and unbundled systems but the management in the bundled system is relatively simple as generation, transmission, and in some cases, distribution systems are managed by one utility. The management of congestion is somewhat more complex in competitive power markets and leads to several disputes.
In the present day competitive power market, each utility manages the congestion in the system using its own rules and guidelines utilizing a certain physical or financial mechanism.
The limitations of a power transmission network arising from environmental, right-of-way and cost problems are fundamental to both bundled and unbundled power systems. Patterns of generation that result in heavy flows tends to incur greater losses, and to threaten stability and security, ultimately make certain generation patterns economically undesirable.
Hence, there is an interest in better utilization of available power system capacities by installing new devices such as Flexible AC Transmission Systems (FACTS). FACTS devices by controlling the power flows in the network without generation rescheduling or topological changes can improve the performance considerably.
The insertion of such devices in electrical systems seems to be a promising strategy to decrease the transmission congestion and to increase available transfer capability. Using controllable components such as controllable series capacitors line flows can be changed in such a way that thermal limits are not violated, losses minimized, stability margins increased, contractual requirement fulfilled etc, without violating specific power dispatch. The increased interest in these devices is essentially due to two reasons. Firstly, the recent development in high power electronics has made these devices cost effective and secondly, increased loading of power systems, combined with deregulation of power industry, motivates the use of power flow control as a very cost effective means of dispatching specified power transactions. It is important to ascertain the location for placement of these devices because of their considerable costs.
A method to determine the optimal location of TCSC was presented in this paper. The approach is based on the sensitivity of the reduction of total system real power loss.
Problem Formulations
Optimal Power Flow (OPF) is defined as the process of allocating generation levels to the thermal generating units in service within the power system, so that the system load is supplied entirely and most economically. The objective of the OPF problem is to calculate, for a single period of time, the output power of every generating unit so that all demands are satisfied at minimum cost, while satisfying different technical constraints of the network and the generators. The problem can be modeled by a system which consists of ng generating units connected to a single bus-bar serving an electrical load PD. The input to each unit shown as Fi, represents the generation cost of the unit. The output of each unit Pi is the electrical power generated by that particular unit. The total cost of the system is the sum of the costs of each of the individual units. The essential constraint on the operation is that the sum of the output powers must equal the load demand.[1]
The standard OPF problem can be described mathematically as an objective with two constraints as:
|
|
(1) |
Subject to the following constraints:
|
|
(2) |
|
Pi(min) ≤ Pi ≤ Pi(max), i =1 ... ng |
(3) |
where Pi(min) and Pi(max) are the minimum and maximum generating limits, respectively, for plant i.
In a large interconnected network where power is transmitted over long distances with low load density areas, transmission losses are a major factor and effect of transmission losses is to express the total transmission loss as a quadratic function of the generator power outputs. The simplest quadratic form is:
|
|
(4) |
The coefficients Bij are called loss coefficients or B-coefficients. B-coefficients are assumed constant and reasonable accuracy can be expected provided the actual operating conditions are close to the base case where the B-constants were computed.
Using the Lagrange multiplier and adding additional terms to include the inequality constraints, we obtain:
|
|
(5) |
The minimum of this unconstrained function is found at the point where the partials of the function to its variables are zero.
|
|
(6) |
Methods to Implementation the TCSC in Power Flow
The CSCs (Controlled Series Capacitor) allow to the operators a better manage of the power flow through a transmission line.
This is useful especially when an irregular power distribution between various transmission circuits leads to an overload and forces the operator to reduce the use capacity of certain lines. The CSCs are an effective means to improve the transfer capacity of the transmission lines. The degree of compensation can be controlled to minimize the system losses during its normal operation. Analyze of a TCSC circuit and its principal functionalities. Since the fundamental components of the voltage and the current are controllable, the TCSC becomes similar to controllable impedance, which is the result of the parallelization of the equivalent reactance of a TCR component and a capacity [2].
Let us note:
|
ZTCSC = jXTCSC |
(7) |
The TCR equivalent impedance with
|
|
(8) |
and the capacity impedance by
|
ZC = -jXC |
(9) |
where Z = line impedance; j = complex number; X = reactance line.
We can write
|
|
(10) |
and
|
|
(11) |
Assume that a TCSC device is placed between two nodes k and m as illustrated in Figure 1. If the losses are neglected, the power P injected into the TCSC starting from the generation node k is equal to that injected by the TCSC in the load node m. The TCSC model represented in Figure 1 is described by the system of Eq. 11.
|
P = -VkVmBesin(θk- θm) Qk = VkVmBecos(θk- θm) – Vk2Be Qm = VkVmBecos(θk- θm) – Vm2Be Be = 1/XC – [2(π-α)+sin2α]/(πXL) √(P2 + Q2) = ICk θk = θm +δt |
(12) |
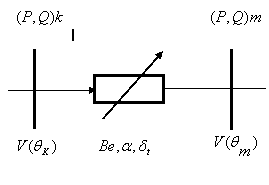
Figure 1. Models TCSC in a Power Flow
Test Results and Discussion
Study of TCSC Controller in the Power System
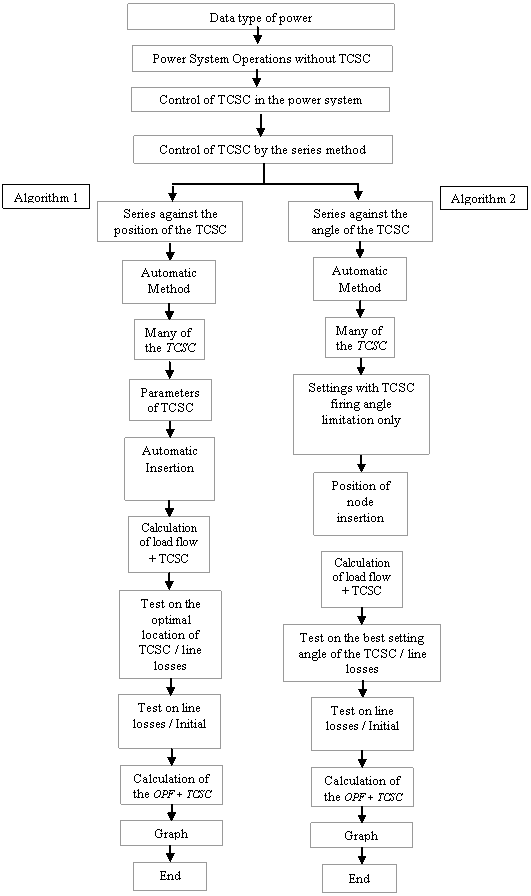
We wanted to close more control real practice, that is to say that the program has the following stages:
1) Analyze the network to be studied;
2) Calculate the power flow and optimization;
3) Sort lines of the network studied in descending order;
4) Less and display a list of long lines, for a percentage of 40;
5) Can offer different options in this case study of TCSC controller in the electric power system
Case 1: «Control series per automatic position»
In the first option, we introduced the parameters of a controller TCSC1 (Thyristor controlled Series Capacitors), more precisely, we have the choice and the possibility of modifying the parameters: XL, XC, αmin, αmax and the angle of starting α. But is with the algorithm to calculate, sort and locate then to post the best site of the TCSC in the studied network with 26 buses (Table 1 & 2). We named this handling: “Control series per automatic position”.
§ Frequency: ƒ = 50 Hz
§ Reactance inductive: XL1 = 0.003 p.u.
§ Reactance capacitive: XC1 = 0.001 p.u.
§ Angle alpha α: Effect capacitive:
§ α1min = 142°, α1max = 180°, α1 = 143°
Table1.Total loss of the system, total cost and the lambda factor of a network of IEEE 26 nodes
|
Results |
Without TCSC |
with TCSC1(Automatic) |
Best locate (k-m) |
|
Total losses (MW) |
12.807 |
12.7786 |
(16-17) |
|
Total cost ($ / h) |
15447.72 |
15447.38 |
(16-17) |
|
Lambda λ ($/ MWh) |
13.538113 |
13.537820 |
(16-17) |
Table2. Optimal Power Generator System IEEE 26 nodes
|
Optimal Power Generated (Mw) |
Without TCSC |
with TCSC1(Automatic) |
Best locate (k-m) |
|
PG1 opt |
447.6919 |
447.5630 |
(16-17) |
|
PG2 opt |
173.1938 |
173.1583 |
(16-17) |
|
PG3 opt |
263.4859 |
263.6850 |
(16-17) |
|
PG4 opt |
138.8142 |
138.9175 |
(16-17) |
|
PG5 opt |
165.5884 |
165.4741 |
(16-17) |
|
PG26 opt |
87.0260 |
86.9740 |
(16-17) |
The study of TCSC controller in the electric power system has been applied to a larger network, to observe the behavior of the program.
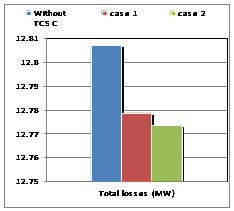
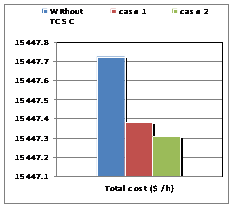
For the "Serial Control by Position Automatically", where a TCSC controller, the total losses of the system decreased to an optimum location of the controller in the line (16-17), resulting in a significant decrease cost factor and lambda.
Case 2: «Control Series per Automatic adjustment of Angle»
The second option introduces a controller TCSC1 (Thyristor controlled Series Capacitors), where we have the choice to change the values: XL, XC, αmin, αmax and the site, this sum of money must be selected according to the list posted by the program of the longest lines. But is with the algorithm to regulate, sort and locate then to post best the angle of starting of controller TCSC in the studied network with 26 buses (Tables 3 & 4). We named this handling: “Control Series per Automatic adjustment of Angle”.
§ Frequency: ƒ = 50 Hz
§ Reactance inductive: XL1 = 0.003 p.u.
§ Reactance capacitive: XC1 = 0.001 p.u.
§ Angle alpha α: Effect capacitive:
§ α1min = 142°, α1max = 180°
Table3. Total loss of the system, total cost and the lambda factor of a network of IEEE 26 nodes
|
Results |
Without TCSC |
with TCSC1 (Automatic) |
Best angle (degree) |
|
Total losses (MW) |
12.807 |
12.7734 |
174.3 |
|
Total cost ($ / h) |
15447.72 |
15447.31 |
174.3 |
|
Lambda λ ($/ MWh) |
13.538113 |
13.537765 |
174.3 |
Table4. Optimal Power Generator System IEEE 26 nodes
|
Optimal Power Generated (Mw) |
Without TCSC |
with TCSC1(Automatic) |
Best angle (degree) |
|
PG1 opt |
447.6919 |
447.5399 |
174.3 |
|
PG2 opt |
173.1938 |
173.1522 |
174.3 |
|
PG3 opt |
263.4859 |
263.7205 |
174.3 |
|
PG4 opt |
138.8142 |
138.9359 |
174.3 |
|
PG5 opt |
165.5884 |
165.4535 |
174.3 |
|
PG26 opt |
87.0260 |
86.9648 |
174.3 |
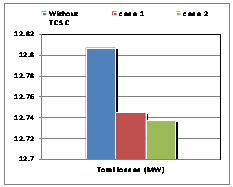
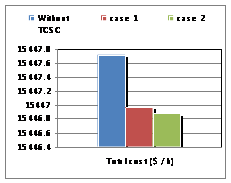
In the simulation, the program changes its objective. We need to insert the TCSC in the network, where we indicated the values of reactance XL, XC, the limits of the firing angle and location of insertion. The need for the program is to locate the best angle adjustment within the limits imposed. In this second algorithm, called "Serial Control by Automatic setting angle, we inserted a TCSC controller in the line already detected by Algorithm 1 which is the line (16-17), so we have greatly improved the system for who found a good fit alpha = 174.3 degrees (Figures 3-5).
|
Figure 2. Total losses for IEEE 26-buses |
Figure 3. Total costs for IEEE 26-buses |
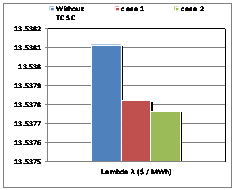
Figure 4. Lambda factor for IEEE 26-buses
Case 1: «Control series per automatic position»
For the same option 1, we introduced now two Thyristors controllers’ series capacities into the network with 26 buses (Tables 5 & 6), for the following parameters:
§ Frequency: ƒ = 50 Hz
§ Reactance inductive: XL1 = 0.003 p.u.
§ Reactance capacitive: XC1 = 0.001 p.u.
§ Reactance inductive: XL2 = 0.002 p.u.
§ Reactance capacitive: XC2 = 0.001 p.u.
§ Angle alpha α: Effect capacitive: α 1min = 142°, α1max = 180°, α1= 143°, α2= 143°
Table 5. Total loss of the system, total cost and the lambda factor of a network of IEEE 26 nodes
|
Results |
Without TCSC |
with TCSC1 and TCSC2 (Automatic) |
Best locate (k-m) |
|
Total losses (MW) |
12.807 |
12.7446 |
(16-17) |
|
Total cost ($ / h) |
15447.72 |
15446.96 |
(16-17) |
|
Lambda λ ($/ MWh) |
13.538113 |
13.537455 |
(16-17) |
Table 6. Optimal Power Generator System IEEE 26 nodes
|
Optimal Power Generated (Mw) |
Without TCSC |
with TCSC1 and TCSC2 (Automatic) |
Best angle (degree) |
|
PG1 opt |
447.6919 |
447.4143 |
(16-17) |
|
PG2 opt |
173.1938 |
173.1197 |
(16-17) |
|
PG3 opt |
263.4859 |
263.9128 |
(16-17) |
|
PG4 opt |
138.8142 |
139.0345 |
(16-17) |
|
PG5 opt |
165.5884 |
165.3404 |
(16-17) |
|
PG26 opt |
87.0260 |
86.9163 |
(16-17) |
In the same option, we have introduced two TCSC controllers; the total losses of the system have dropped dramatically compared to the initial state, the remark as to the cost factor and the lambda. This decrease is obtained for the same optimal location detected by the program that is the line (16-17), the latter result validates the theory of location of FACTS series.
Case 2: «Control Series per Automatic adjustment of Angle» (Tables 7 & 8)
§ Frequency: ƒ = 50 Hz
§ Reactance inductive: XL1 = 0.003 p.u.
§ Reactance capacitive: XC1 = 0.001 p.u.
§ Reactance inductive: XL1 = 0.002 p.u.
§ Reactance capacitive: XC1 = 0.001 p.u.
§ Angle alpha α: Effect capacitive: α1min = 142°, α1max = 180°, α2min = 142°, α 2max = 180°
Table 7. Total loss of the system, total cost and the lambda factor of a network of IEEE 26 nodes
|
Results |
Without TCSC |
with TCSC1 and TCSC2 (Automatic) |
Best angle (degree) |
|
Total losses (MW) |
12.807 |
12.7372 |
147.7 |
|
Total cost ($ / h) |
15447.72 |
15446.88 |
147.7 |
|
Lambda λ ($/ MWh) |
13.538113 |
13.537374 |
147.7 |
Table 8. Optimal Power Generator System IEEE 26 nodes
|
Optimal Power Generated (Mw) |
Without TCSC |
with TCSC1 and TCSC2 (Automatic) |
Best angle (degree) |
|
PG1 opt |
447.6919 |
447.3833 |
147.7 |
|
PG2 opt |
173.1938 |
173.1121 |
147.7 |
|
PG3 opt |
263.4859 |
263.9599 |
147.7 |
|
PG4 opt |
138.8142 |
139.0585 |
147.7 |
|
PG5 opt |
165.5884 |
165.3122 |
147.7 |
|
PG26 opt |
87.0260 |
86.9047 |
147.7 |
The insertion of two TCSC controllers in the same line (16-17), gave results much more important with an angle of alpha = 147.7 degrees leveling found by the algorithm 2 (Figures 5-7).
|
Figure 5. Total losses for IEEE 26-buses |
Figure 6. Total costs for IEEE 26-buses |
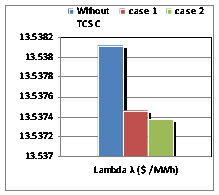
Figure 7. Lambda factor for IEEE 26-buses.
Conclusion
A new OPF problem formulation has been presented to include the effects of the FACTS devices and the specified power flow control constraints. This formulation may simulate the enhanced operation economics and security in future power systems which have TCSC devices with sophisticated power control. A two-stage approach has been proposed to solve this problem. The proposed approach separates the non-linear optimization problem into two sub problems. The first sub problem is a power flow control problem and the second sub problem is an OPF problem. The two sub problems are solved iteratively until a stop criterion is reached. This approach has been tested on an adapted IEEE 26-bus test system and sample studies presented to show the efficiency of the proposed method. Test results of the TCSC controller with our “FACTS Programmer” demonstrated the satisfactory control performance and robustness of the TCSC controller implemented.
References
1. Abdel-Moamen M.A., Narayana P.P., Newton-Raphson TCSC model for the power flow solution of practical power networks, IEEE Power Engineering Society Summer Meeting, 2002, 3, p. 1488-1493.
2. Narayana P.P., Abdel-Moamen M.A., Praveen-Kumar B.J., Optimal location and initial parameter settings of multiple TCSCs for reactive power planning using genetic algorithm, IEEE Power Engineering Society General Meeting, 2004, 1, p.1110-1114.
3. Radu D., Besanger Y., A multi-objective genetic algorithm approach to optimal allocation of multi- type FACTS devices for power system security, IEEE Power Engineering Society General Meeting, 2006, pp. 8.
4. Saravanan M., et al., Application of PSO technique for optimal location of FACST devices considering system loadability and cost of installation, Power Engineering Conference, 2005, 2, p. 716-721.
5. Slochanal S.M.R., et al., Application of PSO technique to find optimal settings of TCSC for static security enhancement considering installation cost, Power Engineering Conference, 2005, 5-A(3), p. 244-251.
6. Radu D., Besanger Y., Blackout Prevention by Optimal Insertion of FACTS Devices in Power Systems, In proc. IEEE FPS 2005 International Conference on Future Power Systems, 16-18 November 2005.
7. Lu Y., Abur A., Static security enhancement via optimal utilization of Thyristor-Controlled Series Capacitors, IEEE Trans. Power System, 2002, 17, p. 324-329.
8. Xia Y., Song Y.H., Sun Y.Z., Power flow control approach to power systems with embedded FACTS devices, IEEE Trans. Power Syst. vol. 17, no. 4, pp. 943–950, November 2002.
9. Li W.L., Zhang Z.H., Jing Y.W., Liu X.P., Nonlinear robust control based on adaptive backstepping design for TCSC, Control Theory Appl., 2005, 22(1), p. 153-156 (in Chinese).
10. Li W.L., Jing Y.W., Dimirovski G.M., Liu X.P., Robust nonlinear control of TCSC for power system via adaptive back-stepping design, IEEE Proc. Control Theory Appl., 2003, 1, p. 23-25.
11. Fuerte-Esquivel C., Acha E., Ambriz-Perez H., A thyristor controlled series compensator model for the power flow solution of practical power networks, IEEE Trans. Power Syst., 2000, 15(1), p. 58-64.
12. Ambriz-Perez H, Acha E, Fuerte-Esquivel CR., Advanced SVC model for Newton–Raphson Load Flow and Newton optimal power flow studies, IEEE Trans Power Syst 2000, 15(1), p. 129-36.
13. Chung T.S., Li Y.Z., A hybrid GA approach for OPF with consideration of FACTS devices, IEEE Power Eng Rev 2001, 21(2), p. 47-50.
14. Ongsakul W., Bhasaputra P., Optimal power flow with FACTS devices by hybrid TS/SA approach, Electr. Power Energ. Syst., 2002, 24, 851-857.