Multi-Drive Paper System Control Based on Multi-Input Multi-Output PID Controller

Boumediène ALLAOUA^*, Abdellah LAOUFI and Brahim GASBAOUI

Bechar University, Faculty of Sciences and Technology, Department of Technology, B.P 417 BECHAR (08000) Algeria.

E-mail(s): elec_allaoua2bf@yahoo.fr^*, laoufi_ab@yahoo.fr, gasbaoui_2009@yahoo.com,

(*Corresponding author )

Abstract

Paper industries require several drives for paper processing. Electronic synchronization has to be ensured for quality of produced paper rolls. Several control strategies of multi-input multi-output (MIMO) system (multivariable system) have been suggested based on robust control or electronic emulation of mechanical line shaft. In this paper, a multivariable proportional-integral-derivative (PID) controller applied on multi-drive paper system (MDPS). The proposed controller has superior feature, including easy implementation, stable convergence characteristics and very good computational performances efficiency. The multivariable PID controller is modeled in MATLAB environment. The speed control of MDPS (in our case is a triple drive system) based on multivariable PID is more proficient in improving the speed loop response stability, the steady state error is reduced, the rising time is perfected and the disturbances do not affect the performances of driving motors with no overtaking.

Keywords

Multi-drive Paper System; Multivariable PID Control; MIMO system; MDPS Speeds Control.

Introduction

Paper industries require several drives for paper processing. In the past, a single mechanical line shaft was used for all drives [1]. Nowadays independent drives are used [2]. Electronic synchronization has to be ensured for quality of produced paper rolls [3]. Several control strategies have been suggested based on robust control [4, 5] or electronic emulation of mechanical line shaft [1, 6].

In industry, the paper, plastic and other thin elastic materials are often employed for the manufacture of commercial products by employing a continuous process [4]. In this case, paper or any other material is typically unrolled of a large roll by using a series of rollers and a rewinder, formant what is called enchainment. The enchainment main goal is the affectation of the process to transfer the material with a maximum speed and a possible minimum damages. The paper can be rolled onto a cylindrical shaft for storage and easy supply to later processing stages such as testing, cutting, and lamination. Alternatively, the material would require very large manufacturing facilities or cutting of the material into smaller sections. In addition to tension, the velocity of the paper passing though a processing stage is of paramount importance. If the velocity is not within specifications, product quality is again compromised [7], for this reason the control will be necessary.

The proposed system is composed of two paper rollers and a tensioning roller. This multi-drive system set-up will be used to study the effect of voltage sags on such a system [8]. Such a system requires a complex control of the three drives in order to avoid paper damage, and good dynamic performance. Thus, the tensions of both paper bands have to be regulated. Moreover, the winding velocity requires a precise control in order to ensure a high quality of the final paper roll.

The control problem is particularly difficult because of the nonlinearities of the model [4, 5, 9, 10], strong and weak interactions among the subsystems, the uncertainties in the parameters and the various disturbances that can act upon the system. The multivariable control strategy is complex when the multi-drive system is complex; a lot of variables of control are tacking in consideration too. In our case the proposed controller is multivariable PID.

Proportional-integral-derivative (PID) control offers the simplest and yet most efficient solution to many real-world control problems. Three-term functionality of PID controller covers treatment of both transient and steady state responses. The popularity of PID control has grown tremendously, since the invention of PID control in 1910 and the Ziegler–Nichol’s straight forward tuning method in 1942. With the advances in digital technology, the science of automatic control now offers a wide spectrum of choices for control schemes such as adaptive control [11], neural network control [12] and fuzzy logic control [13]. However more than 90% of industrial controllers are still implemented based around PID control algorithms, as no other controllers match the simplicity, clear functionality, applicability and ease of use offered by the PID controllers [14].

Several approaches have been reported in literature for tuning the parameters of PID controllers. Ziegler-Nichols and Cohen-Coon are the most commonly used conventional methods for tuning PID controllers and neural network, fuzzy based approach, neuro-fuzzy approach and evolutionary computation techniques are the recent methods [15].

In this paper, a control structure is suggested for the studied triple drive paper system. This multivariable PID control is deduced and leads to good dynamic performance for paper tensions and winding velocity. Because of a natural decoupling induced by this methodology, classical controller can be used instead of robust control strategy or mechanical emulation. However the suggested control structure requires many controllers and measurements or estimations. Simulation results are provided for start-up, which is a sensitive case in such an application.

Description of the Triple Drive System

This section is dedicated for the presentation of the triple drive system (MDPS). In the industry of paper [16, 17] the winding systems are very present. The test system constitutes three motors forming the winding system, every motor has an independent alimentation and an indirect field oriented control (IFOC) [18, 19]; the motors are coupled mechanically by a band whose tension is adjustable by the control of the last motors. This system is composed two different parts; Figure 1 shows the electrical part of the triple drive system and Figure 2 shows the mechanical part of the triple drive system.

Electrical Part

Induction machines are chosen as in many industrial applications (Figure 2). Each machine is supplied by its own voltage source inverter (VSI). The three VSI share a common DC bus, which is obtained from the grid, a diode rectifier, a capacitor set and every motor has an IFOC.

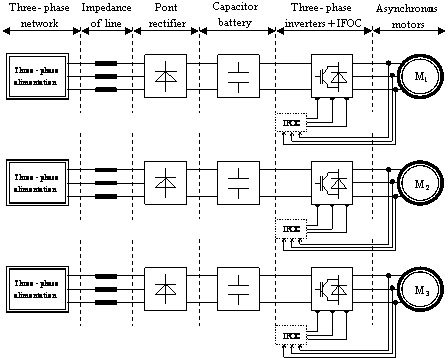
Figure 1. Electrical part of the triple drive system

The model equations of the motors and the tensions between them are:

                        (1)

                                                                       (2)

                                                             (3)

                                                       (4)

                                                               (5)

Table 1 illustrates the used symbols.

Table 1. Used symbols

Symbols	Designations	Units
Cemand Cr	Electromagnetic couple and Resistive torque.	N·m
V	Tape speed of paper.	m/ sec
H	Thickness of paper.	m
J0	Vacuum inertia.	kg·m^2
E	Band Young modulus.	N/m²
S	Enchainment section.	m²
Vi (i=1,3)	Linear velocity of roller i.	m/ sec
Ωi (i=1,3)	Rotation speed of the roller i.	rad/ sec
Ri (i=1,3)	Ray of the roller i of paper.	m
Ji (i=1,3)	Inertia moment of the roller i.	kg·m^2
fi (i=1,3)	Coefficient of viscous friction of the roller i.	N·m·sec /rad
Ti (i=2,3)	Mechanical tension enters the rollers i and i+1.	N
li (i=1,2)	Enchainment length enters the rollers i and i+1.	m

Mechanical Part

The mechanical part is composed of three electric motors (Figure 1), the machines M₁ and M₃ lead to the unwinding and winding of the paper. The machine M₂ drives a nip stage and pinching the product. Two paper band sections are defined: the band between the motors M₁ and M₂, and the band between M₂ and M₃.

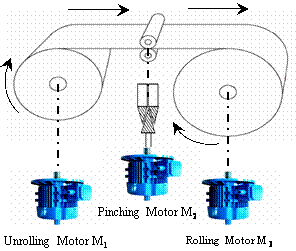
Figure 2. Mechanical part of the triple drive system

Multivariable PID Controller Structure for MIMO Systems

A standard PID controller structure is also known as the ‘‘three-term” controller [14, 15, 20], whose transfer function is generally written in the ideal form in (6) or in the parallel form in (7)

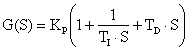(6)

                                                                                       (7)

where K_P is the proportional gain, T_I is the integral time constant, T_D is the derivative time constant, K_I =K_P /T_I is the integral gain and K_D =K_PT_D is the derivative gain. The ‘‘three-term” functionalities are highlighted below [20, 21].

The terms K_P , T_I and T_D definitions are:

§ The proportional term: providing an overall control action proportional to the error signal through the all pass gain factor.

§ The integral term: reducing steady state errors through low frequency compensation by an integrator.

§ The derivative term: improving transient response through high frequency compensation by a differentiator.

Figure 3. A multivariable PID control system

Consider a multivariable PID control structure as in Fig. 3, where, desired output vector:

;

Actual output vector:

;

Error vector:

;

Control input vector:

;

n×n Multivariable processes or MIMO system:

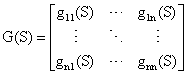                                                                                   (8)

n×n Multivariable PID controller:

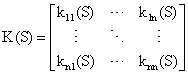                                                                                   (9)

In this work, decoupled multivariable PID controller is considered. So K(S) becomes:

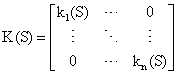                                                                                     (10)

The form of k_i(S) is either in (6) or (7). In this work, ‘‘parallel form” of PID controller in (7) is used and can be rewritten as:

                                                                                    (11)

For convenience, let , represents the gains vector of i-th diagonal sub PID controller in K(S) .For multivariable PI controller, k_i(S) in (11) can be rewritten as

                                                                                                  (12)

 represents the gains vector of the i-th diagonal sub PI controller in K(S).

Computer Simulation Results

From the state equations, we can construct the model with the environment MATLAB 7.6 (R2008a) in Simulink version 7.1. To evaluate the performances of the system we carried out digital simulations under the following conditions:

§ Starting with level speed application of 50 Rad/Sec.

§ The motor M₁ role to unrolling the roller of ray R₁ (R₁=2.25 m).

§ The motor M₂ makes the pinching of the band. 

§ The motor M₃ role to rolling the roller of ray R₃.

§ To turn off slightly the several motors at the same time of system until where the ray to regulate reached a desired value (example: R₃=0.8 m), by injecting a null speed reference.

§ The simulation results are obtained for 22 seconds range time.

The Figures 4, 5 and 6 demonstrate that the adjustment using multivariable PID Controller gives satisfactory results to the MDPS speeds control:

§ The three motors rotational speeds (Ω₁, Ω₂ and Ω₃) follow the reference speed.

§ It is noticed that the electromagnetic couple C_em follows the resistive torque value Cr.

§ It is also noticed that the inertia moment J reduce with the reduction in the ray R and augment with its augmentation.

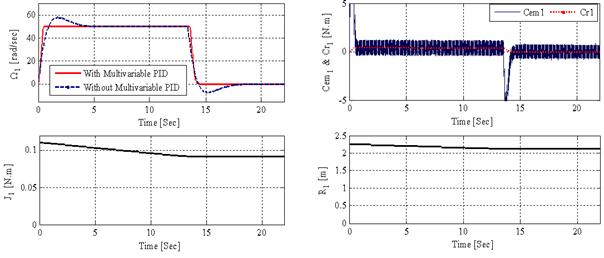
Figure 4. Simulation results of the first motor M₁ (Unrolling Motor)

The general objective of the transport processes, winding and unwinding allows with insurance which the unit works in harmony and synchronism, especially to ensure a good quality of the treatment and rewinding of the product.

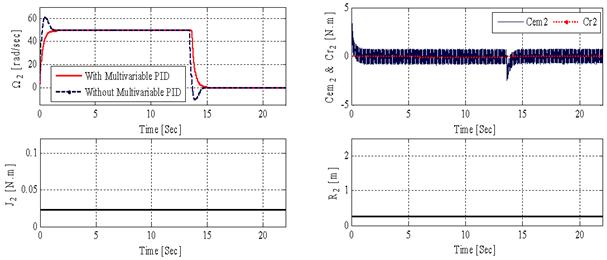
Figure 5. Simulation results of the second motor M₂ (Pinching Motor)

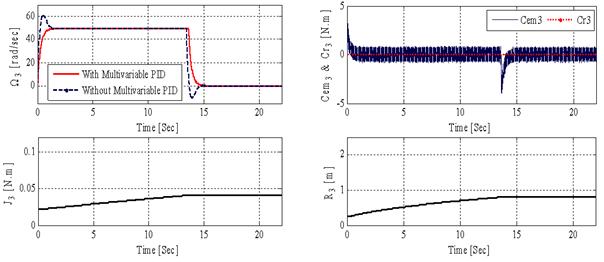
Figure 6. Simulation results of the third Motor M₃ (Rolling Motor)

Conclusions

In this paper, the speeds of three motors forming a MDPS system are controlled by multivariable PID controller. Performance evaluation of multivariable PID controller for winding system in particular was presented, significant improvement of the systems and of the controls of these systems is still both possible and desirable to satisfy the need for higher processing speeds and increased constraints on accuracy.

This work enabled us to contribute a technological share for the MDPS system of high efficiency. The simulation results show well the system steps and the operation stages. The multivariable PID controller advantages are the effects compensation of non linearity, to ensure a good internal and high stability performance of the system with a negligible starting error. The multivariable PID controller is the best which presented satisfactory performances and possesses good robustness (no overshoot, minimal rise time, Steady state error = 0).

Appendix

Table 1. Parameters of the asynchronous motors.

Designations	Abbreviation	Value	Units
Nominal power	Pn	3.5	kw
Nominal voltage	Vn	380	V
Nominal power-factor	cosφn	0.8	––
Nominal Speed	Nn	1428	tr/min
Nominal frequency	F	60	Hz
Nominal current	In	9.31	A
Stator resistance	Rs	6.85	W
Rotor resistance	Rr	4.85	W
Cyclic inductance stator	Ls	0.374	H
Cyclic Inductance rotor	Lr	0.374	H
Mutual Inductance	Lm	0.358	H
Many pairs of poles	P	2	––
Inertia Moment	J	0.06	kg/m^2
Coefficient of friction	fc	0.009	N.m.sec/rad

References

1. Valenzuela M., Lorenz R., Electronic line-shafting control for paper machine drives, IEEE Trans. on Industry Applications, 2001, 37(1), p. 158-164.

2. Jaego A., Nowacki Z., The technological requirements in paper industry refer multimotor drives, in Proc. of EPE'99, Lausanne, September 1999.

3. Huang C., Shong L., Control of tension and line speed in fabric finishing, Textile Research Journal, 1999, 69(10), p. 714-719.

4. Koç H., Knittel D., de Mathelin M., Abba G., Modelling and robust control of winding systems for elastic webs, IEEE Transactions on Control Systems Technology, 2002, 10(2), p. 197-208.

5. Charlemagne S., Bouscayrol A., Belkhodja S., Hautier J. P., Flatness based control of non-linear textile multimachine process, in Proc. of EPE'03, Toulouse (France), September 2003.

6. Perez-Pinal F., Claderon G., Araujo-Vargas I., Relative coupling strategy, in Proc. of IEEE-IEMDC'03, Madison (USA), June 2003.

7. Geddes J. E., Postlethwaite M., Improvements in product quality in tandem cold rolling using robust multivariable control, IEEE Trans. Contr. Syst. Technol., 1998, 6, p. 257-267.

8. Sicard P., Elouariachi N., Lahaie S., Characterization of sensitivity to voltage sags of mechanically coupled induction motors, in Proc. of ElectrIMACS’2002, Montreal (Canada), August 2002.

9. Wankam Y. D., Sicard P., Bouscayrol A., Maximum control structure of a five-drive paper system using Energetic Macroscopic Representation, IEEE IECON’2006, Special Session Graphical Description for Modeling and Control Power Systems, Paris, 2006, 6, p. 5332-5337.

10. Mokhtari F., Sicard P., Hazzab A., Cascade Decentralized Nonlinear PID Control of Continuous Production Processes, ELECTRIMACS’08, Quebec, 2008.

11. Astrom K. J., Wittenmark B., Adaptive control, 2nd ed. Addison Wesley, 1995.

12. Fukuda T., Shibata T., Theory and application of neural networks for industrial control systems, IEEE Transactions on Industrial Electronics, 1992, 39(6), p. 472-489.

13. Lee C.C., Fuzzy logic in control systems: Fuzzy logic controller – Part I and II, IEEE Transactions on Systems Man and Cybernetics, 1990, 20(2), p. 404-435.

14. Ang K.H., Chang G., Yun Li, PID control system analysis, design and technology, IEEE Transaction on Control System Technology, 2005, 13(4), p. 559-577.

15. Astrom K.J., Hagglund T., PID controllers: theory, design, and tuning, 2nd ed. Instrument society of America, 1995.

16. Jagieo J., Nowachi Z., The Technological Requirements in Paper Industry Multimotor Drive, EPE’99, Lausane, 1999.

17. Valenzuela A., Lorenz R., Electronic Line Shafting Control for Paper Drives, IAS 2000, Rome, 2000.

18. Zhang Y., Jiang Z., Yu X., Indirect field-oriented control of induction machines based on synergetic control theory, Power and Energy Society General Meeting - Conversion and Delivery of Electrical Energy in the 21st Century, IEEE 2008, 20-24 July 2008, pp. 1-7.

19. Kim D.H., GA-PSO based vector control of indirect three phase induction motor, Applied Soft Computing, 2007, 7, p. 601-611.

20. Wang J.S., Zhang Y., Wang W., Optimal design of PI/PD controller for non-minimum phase system, Transactions of the Institute of Measurement and Control, 2006, 28(1), p. 27-35.

21. Bingul Z., A new PID tuning technique using differential evolution for unstable and integrating processes with time delay, ICONIP, Proceedings Lecture Notes in Computer Science, 2004, 3316, p. 254-260.