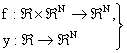On Error Estimation in Runge-Kutta Methods
Ochoche ABRAHAM1,*, Gbolahan BOLARIN2
1Department of Information Technology, 2Department of Mathematics & Statistics Federal University of Technology, Minna, Nigeria
E-mails: abrahamo@member.ams.org, gbolahan.bolarin@gmail.com
* Corresponding author: abrahamo@member.ams.org
Received: 16 December 2010/ Accepted: 17 March 2011 / Published: 24 June 2011
Abstract
It is common knowledge that the bounds for the local truncation errors in Runge-Kutta methods do not form a suitable basis for monitoring the local truncation error. In this paper, we have presented an established process by which a readily computable estimate of the local truncation error can be obtained without need to obtain exact solutions or solve problems analytically.
Keywords
Error; Estimation; Runge-Kutta; Richardson Extrapolation; Exact, Approximate.
Introduction
Historically, differential equations have originated in chemistry, physics and engineering. More recently, they have also arisen in medicine, biology, anthropology, and the like. However, we are going to restrict ourselves to Ordinary Differential Equations (ODE), with special emphasis on Initial Value Problems (IVP), so called because the condition on the solution of the differential equation, are all specified at the start of the trajectory i.e. they are initial conditions [1].
In [2], it was stated that among the models using differential equations, ordinary differential equations (ODE) are frequently used to describe various physical problems, for example, motions of the planets in a gravity field like the Kepler problem, the simple pendulum, electrical circuits and chemical kinetics problem. An ODE has the form:
|
y¢(x) = f(x, y(x)) |
(1) |
where x is the independent variable which often refers to time in a physical problem and the dependent variable y(x), is the solution. Since y(x) could be an N dimensional vector valued function, the domain and range of the ordinary differential equation, f and the solution y are given by:
|
|
(2) |
The above ODE is called ‘non-autonomous’ because f is a function of both x and y. however, by simply introducing an extra variable, which is always exactly equal to x, it can be easily rewritten in an equivalent ‘autonomous’ form as:
y¢(x) = f(y(x))
where f is a function of y only.
Unfortunately, many problems involving ODE cannot be solved exactly. This is why the ability to numerically approximate these methods is so important [2].
Numerical solution of ODEs is the most important technique ever developed in continuous time dynamics. Since most ODEs are not soluble analytically, numerical integration is the only way to obtain information about the trajectory. Many different methods have been proposed and used in an attempt to solve accurately, various types of ODEs. However, there is a handful of methods known and used universally (i.e. Runge-Kutta, Adam-Bashforth-Moulton and Backward Difference Formulae). All these discretise the differential system to produce a difference equation or map [3].
The methods, obtain different maps from the same equation, but they have the same aim; that the dynamics of the maps, should correspond closely, to the dynamics of the differential equation. From the Runge-Kutta family of algorithms, come the most well-known and used methods for numerical integration [4].
With the advent of computers, numerical methods are now an increasingly attractive and efficient way to obtain approximate solutions to differential equations that had hitherto proved difficult, even impossible to solve analytically. However, for this work, we are particularly interested in the class of methods first proposed by David Runge (1856-1927) [5], a German mathematician and physicist, and further extended by another German mathematician called Wilhelm Kutta (1867-1944) [6] to systems of equation; a method commonly referred to as the Runge-Kutta method.
Material and Method
The Dynamics of Runge-Kutta Methods
We consider the IVP:
|
y¢ = f(x, y), y(a) = α |
(3) |
The Runge-Kutta methods for the solution of Equation (3), are one-step methods designed to approximate Taylor series methods but have the advantage of not requiring explicit evaluation of the derivatives of f(x, y), where x often represents time (t). The basic idea is to use a linear combination of values of f(x, y) to approximate y(x). This linear combination is matched up as closely as possible, with a Taylor series for y(x) to obtain methods of the highest possible order. It will be supposed that the initial value (x0, y0) is not singular with respect to the equation and that a solution exists, which can be developed in Taylor series. [7]
According to [8], [9], the general S-stage Runge-Kutta method is defined by:
|
|
(4) |
|
|
(5) |
|
|
(6) |
Call k=[k1, k2,…,ks] the slopes, b=[b1, b2,…,bs] the weights, and c=[c1, c2,…,cs] the abscissa.
An s-stage R-K method requires s functions evaluation per step. Each of the functions kr = (x, y, h), r = 1, 2…s may be interpreted as an approximation to the derivative y¢(x) and the function f(x, y, h) as a weighted mean of these approximations. Consistency, demands that ∑sr=1br = 1.
Derivation of an s-Stage Runge-Kutta Method
According to [1], there are three ways of deriving Runge-Kutta methods:
· Taylor series expansion;
· The algebraic concept of rooted trees;
· Computer algebra.
In this paper, our discussions would be on the Taylor series expansion method.
The process of deriving a given R-K method by Taylor series expansion can be summarized into the following three steps:
· Step1:
Obtain the Taylor series expansion of kr (the slopes) defined by:
|
kr = f(zr, yn+h∑s<j=1arjkj) |
(7) |
where: zr = xn + crh, r=1(1)s about the point (xn, yn) in the solution space.
· Step 2:
Insert these expansions and cr(cr= ∑sj=1arj,r=1(1) into the expression for the general S-stage R-K method, given as:
|
fRK = ∑s<j=1bjkj, s≥1 |
(8) |
· Step 3:
Compare the coefficients in powers of h for both the increment function fRK of the Runge-Kutta method given by Equation (8) above and the increment function fT for the Taylor expansion method specified by:
|
|
(9) |
It has been shown [8], [9] and [10], that if these functions agree up to terms in hp, then the process is of order p. The totality of the unknown coefficients {bj, cr, arj, j=1(1s)} normally exceeds the number of equations, leaving us with some free parameters to which we can assign values, [11].
Richardson Extrapolation
One major flaw in the Runge-Kutta methods is that it is quite difficult and complicated to watch errors. According to [8], “bounds for the local truncation errors do not form a suitable basis for monitoring the local truncation error, with a view to constructing a step-control policy similar to that developed for Predictor-Corrector methods. What is needed, in place of a bound, is a readily computable estimate of the local truncation error, similar to that obtained by Milne’s device for predictor-corrector pairs”.
The estimate we are presenting arises from an application of the process of deferred approach to the limit, otherwise known as Richardson extrapolation. This involves solving a problem twice using step sizes h and 2h.
Under the localizing assumption that no previous errors have been made, we may write:
|
y(xn+1) – yn+1 = Tn+1 = φ(xn, y(xn))hp+1+o(hp+2) |
(10) |
where p is the order of the Runge-Kutta method, φ(xn, y(xn))hp+1 is the principal local truncation error.
Next, we will compute y*n+1, a second approximation to y(xn+1), obtained by applying the same method at xn-1 with steplenght 2h. Under the same localizing assumption, it follows that:
|
y(xn+1) – y*n+1 = φ(xn-1, y(xn-1))(2h)p+1+o(hp+2) |
(11) |
and on expanding φ(xn-1, y(xn-1)) about (xn, yn):
|
y(xn+1) – y*n+1 = φ(xn, y(xn)) (2h)p+1+o(hp+2) |
(12) |
On subtracting (10) from (12), we obtain:
y(xn+1) – y*n+1 = (2p+1 – 1)φ(xn, y(xn))hp+1+o(hp+2)
Therefore, the principal local truncation error that is taken as an estimate for the local truncation error may be written as:
|
φ(xn, y(xn))hp+1 = Tn+1 = (y(xn+1) – y*n+1)/(2p+1 – 1) |
(13) |
=>
|
Tn+1=(y(xn+1)-y*n+1)/(2p+1–1) |
(14) |
Equation (14) is a mean of obtaining quick estimates of the local truncation errors in computations using any S-stage Runge-Kutta, without having to obtain the exact solution first.
Numerical Experiments
We will illustrate the viability of Richardson Extrapolation technique represented by Equation (14) by solving the autonomous initial value problem:
y’=x+y; y(0)=1 (Exact solution: yE=2ex-x-1)
at steplenghts h = 0.1 and h = 0.2.
The method we will use for our investigation, is the very efficient six-stage Runge-Kutta method of order five with Butcher tableau:

From now on we will refer to this method as RK65.
Results and Discussions
The results are as presented below:
Table 1. Results for the Numerical Experiment
|
h |
x |
RK65 |
Exact |
Actual Error |
|
|
0.0 |
1.0 |
1.0 |
0.0 |
|
0.1 |
0.1 |
1.110341796 |
1.110341836 |
4.01513E-08 |
|
|
0.2 |
1.242805427 |
1.242805516 |
8.93203E-08 |
|
|
0.3 |
1.399717467 |
1.399717615 |
1.48152E-07 |
|
|
0.4 |
1.583649177 |
1.583649395 |
2.18283E-07 |
|
|
0.5 |
1.79744224 |
1.797442541 |
3.014E-07 |
|
|
0.6 |
2.044237201 |
2.044237601 |
3.99781E-07 |
|
|
0.7 |
2.327504899 |
2.327505415 |
5.15941E-07 |
|
|
0.8 |
2.651081205 |
2.651081857 |
6.51985E-07 |
|
|
0.9 |
3.019205412 |
3.019206222 |
8.10314E-07 |
|
|
1.0 |
3.436562662 |
3.436563657 |
9.94918E-07 |
|
|
0.0 |
1.000000000 |
1.000000000 |
0.000000000 |
|
0.2 |
0.2 |
1.242803057 |
1.242805516 |
2.45932E-06 |
|
|
0.4 |
1.583643388 |
1.583649395 |
6.00728E-06 |
|
|
0.6 |
2.044226595 |
2.044237601 |
1.10058E-05 |
|
|
0.8 |
2.651063934 |
2.651081857 |
1.7923E-05 |
|
|
1.0 |
3.436536293 |
3.436563657 |
2.73639E-05 |
Usually to obtain errors, the exact solutions as well as the numerical approximations are obtained and their difference at each step gives the error at each step. Our intention in this paper is to show that it is indeed possible to obtain such errors without the need to obtain the exact solutions first.
Next, Equation (14) will be used to obtain error estimates that do not depend on the exact solutions.
Recall Equation (14):
Tn+1=(y(xn+1)-y*n+1)/(2p+1–1)
where: yn+1 is the approximate solution with h = 0.1; y*n+1 is the approximate solutions with h = 0.2; p is the order of the method i.e. p = 5.
Hence, Equation (14) becomes:
Tn+1=(y(xn+1)-y*n+1)/63
It must be pointed out that what Equation (14) provides, are estimates, but these estimates give us an idea of the nature and order of the errors we are dealing with and when analytical solutions cannot be obtained, this method is the only option available.
At x = 0.2 : Tn+1 = 1.242805427 - 1.242803057/63=3.7619E-08
At x = 0.4 : Tn+1 = 1.583649177 - 1.583643388/63 = 9.189E - 08
At x = 0.6 : Tn+1 = 2.044237201 - 2.044226595/63 = 1.684E - 07
At x = 0.8 : Tn+1 = 2.651081205 - 2.651063934/63 = 2.74E – 07
At x = 1.0 : Tn+1 = 3.43656362 - 3.436536293/63 = 4.186E - 07
A comparison of the estimated error and the actual error is given in Table 2 below:
Table 2. Summary of Results for Actual Errors and Estimated Errors
|
x |
Actual Error |
Error Estimate |
|
0.2 |
8.90E-08 |
3.76E-08 |
|
0.4 |
2.18E-07 |
9.19E-08 |
|
0.6 |
4.00E-07 |
1.68E-07 |
|
0.8 |
6.52E-07 |
2.74E-07 |
|
1.0 |
9.95E-07 |
4.19E-07 |
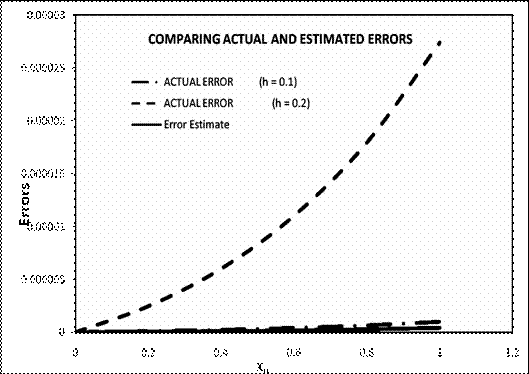
Figure 1. Graph comparing the Actual Errors and Estimated Errors
From Figure 1 we can see from the solution curves that the curve for the error estimates using Richardson extrapolation is very close to the curve of the numerical solution for RK65 for h = 0.1.
The exponents of our estimates compare favourably with that of the actual errors for h = 0.1 (between 10-7 - 10-8). However, for h = 0.2, our error estimates as well as the solution for h = 0.1, are both very far from the actual errors which is a good thing as accuracy is supposed to decreases with increase in steplenght. Therefore our result conforms to reality.
Conclusions
We can thus conclude that when using Runge-Kutta methods to solve non-stiff problems, we do not as necessities need to compute the exact solutions before we can compute errors. Richardson extrapolation provides a viable error estimator that is capable of giving a workable idea of the nature and degree of errors.
As most differential equations are not soluble analytically, exact solutions cannot be obtained and hence it would not be possible to obtain errors for such problems. However, Richardson extrapolation provides an excellent means to get around this problem since exact solutions are not required to obtain error estimates.
References
1. Julyan E.H.C., Piro O., The Dynamics of Runge-Kutta Methods, International Journal of Bifurcation and Chaos, 1992, 2, p. 427-449.
2. Lee J.H.J., Numerical Methods for Ordinary Differential Equations: A Survey of Some Standard Methods, 2004, MSc. Thesis, Univ. of Auckland, New Zeeland.
3. Rattenbury N., Almost Runge-Kutta Methods for Non-Stiff Problems, 2005, Ph.D. Thesis, The Univ. of Auckland, New Zeeland.
4. Butcher J.C., Coefficients for the Study of Runge-Kutta Integration Processes, Journal of the Australian Mathematical Society, 1963, 3, p. 185-201.
8. Lambert J.D., Computational Methods in Ordinary Differential Equations, John Wiley and Sons, USA, 1973, p. 114-116.
9. Lambert J.D., Numerical Methods for Ordinary Differential Systems, John Wiley and Sons, USA, 1991, p. 149-150.