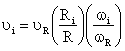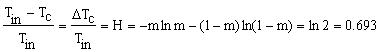Modelling of the Turbulent Effect on the Basis of Thermodynamics
Koros NEKOFAR
Islamic Azad University, Chaloos Branch, Chaloos, Iran
E-mail: nekoufar@iauc.ac.ir
Received: 31 October 2010 / Accepted 28 March 2011 / Published: 24 June 2011
Abstract
The Ranque vortex tube (effect Ranque) is a device by which cold gas can be generated using compressed gas. In this article, the process of gasses’ thermal division in turbulent tubes is described on the basis of thermodynamic theory according to Newtonian time. It means that, at the present work, investigate the possibility of a new approach, developed in the framework of the scientific field macro quantum thermodynamics as an alternative to the classical thermodynamics.
Keywords
Non-local thermodynamic; Ranque effect; Vortex pipe.
Introduction
The phenomenon of two gas streams separated without mechanical assistance was discovered by George J. Ranque in 1933 and was the subject of a US Patent in 1934. The tube later became known as the Ranque vortex tube. Compressed gas, air, enters the device tangentially to create a vortex that travels through a generation chamber. The air is then reflected with a conical valve. The conical valve adjusts the balance of the amount of air that is allowed to escape and the amount that is forced back through the axis of the vortex. This balance is known as the cold fraction. The temperature drop is a function of the ambient temperature, pressure, cold fraction, and flow of compressed gas. Cold exit temperatures can reach as low as -40ºC [1].
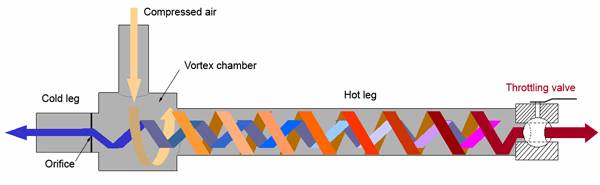
Figure 1. Separation of a compressed gas into a hot stream and a cold stream
Turbulent Ranque effect is a typical macro-quantum phenomenon, which cannot be described by classical theory. About a century of unsuccessful experience in defining this phenomenon based on classical methods testifies to this. There are different explanations for the effect and there is debate on which explanation is best or correct. The explanation of this phenomenon has been the centre of much research since its discovery. There is still no universally adopted theory that explains the effect of the vortex. The vortex tube is considered the result of several simultaneous phenomenons.
Another new approach to solve this problem is using non-local version of thermodynamics, developed in the Moscow State University of Engineering Ecology [2]. The basic idea of non–local thermodynamics is to use quantum entropy, with every quantum defined as equal to Boltzman constant -k. This hypothesis will allow applying thermodynamic energy -kT. Further, correlations of quantum mechanics are used. For brevity purposes, only the relation of energy-time is used here:
|
|
(1) |
Using DЕ=kT in Equation (1) allows establishing the minimum interval macroscopic processes that depend only on temperature:
|
|
(2) |
In addition, radius r and volume V in the environment for time Dt is:
|
|
(3) |
|
|
(4) |
For example, at T=293K, by using Equations (2), (3) and (4) we will receive the following results: Δt=1.3×10-14s; r=3.9×10-6 m; V=2.5×10-16 m3.
Volume V, calculated using the minimum sizes of DЕ, Dt and k, on a physical sense, is the minimum macroscopic volume. The enclosed area by this volume is named macro cell in non-local version of thermodynamics. The macro cell can be considered as shortly living and special physical cluster, over the molecular level in hierarchy of macroscopic system. Characteristic of a macro cell as a physical self-reliant object is that, on the one hand, it is the maximum microscopic volume and quantum mechanics laws apply to it, and on the other hand, is the minimum macroscopic volume, to which apply minimum classical definitions.
Hereafter there is a possibility of simultaneous existence of Boltzman and Planck constants at macro level. For example, in the new approach it has been shown that the ensemble of particles in a macro cell act as a unit and their collective speed at time Dt is υ=(kT/m)1/2.
In other words, in non-local version of thermodynamics, balance is considered as dynamic resilient position and for its maintenance, function of certain forces is required which depend on temperature:
|
|
(5) |
It was on this basis that the Ranque effect was described thermodynamically [3].
Material and Method
For this purpose, we will start with some macroscopic elements in hydrodynamics. In the way that the macroscopic elementary stream will have the maximum section of a macro cell, the connected surface stream will have a thickness of 2r, where r is macro cell radius.
Obviously, macroscopic, the elementary stream will have a radius of R with the maximum section of a macro cell.
Let the ensemble of such elementary streams have a macroscopic and connected surface stream of width b and volume V=2brR, but the attached surface stream with N package will have such volume of Vp=2brRN.
The mass of surface package of stream is calculated from the following relation:
|
M=2brRNρ |
(6) |
where ρ indicates density, and N indicates the number of elementary surface vortexes.
In a vortex tube, the centrifugal force arising in a macroscopic vortex, Equation (6), operates with an angular speed ω:
|
F=Mω2R |
(7) |
Force F as an external force acts on macro cell of non-local version of thermodynamics in which operates resilient force (5). As a result, according to the non-local version of thermodynamics, the macro cell moves from equilibrium to another dynamic equilibrium position, observing the equality of centrifugal force and resilient inertial forces in a macro cell. At resilient equilibrium state of this position, the other macro cell will have a new temperature according to Equation (5). Combining Equations (5) and (7) it results:
|
|
|
Considering m=Vρ and Equation (6) we will have:
|
|
|
As V= (4/3) πr³, ∆t=h/2kT and, r=ch/2kT, it is possible to have the following ratio:
|
Bω2R2Nρ1/2=aT |
(8) |
where a =πсk(2⁄3πсħ)1/2 =0.0337 (m.J)3/2/s.K (a collection of constants).
Thus, the right side of Equation (8) only depends on temperature and some basic constants. Parameters in the left part depend on current vortex’s radius Ri, and so we can write the following expression:
|
|
(9) |
Equations (8) and (9) are the main equations for describing the regime and structural effect of parameters of Ranque vortex tube, which are obtained exclusively, based on macro quantum parameters.
Calculation
One can easily analyze hydrodynamic vortex attached to the tube’s internal wall. For this purpose we may use linear speed in tube’s entrance of vortex tube’s connector, which has been calculated on the basis of entrance section of connector tube’s nozzle and specific efficiency υ=2πRω. Whence ω=υ⁄2πR and finally, from Equation (7) we will get:
|
υ²bNρ1/2=a´T |
(10) |
where, a´=4π²a=1.3304 (m.J)3/2/s.K., i.e. in the condition of applying optional linear speed, entrance stream of Ranque effect is determined by dependent package bN and density ρ.
Amount of selection of cold (hot) stream should be considered separately. Selection affects hydrodynamic stream. So we will consider the linear speed at tube’s wall equal to υR=2πRωR and υi=2πRiωi. Dividing υR on υi we’ll have:
|
|
(11) |
The ratio of first relation decreases as the radius of vortex decreases, but the second ratio may increase which results in the decrease or increase of external stream’s temperature. This naturally influences selection of hot stream. Therefore, selection influence can lead to a minimum of external stream’s temperature and a maximum of division efficiency.
If we arrive at the conclusion that thermodynamic nature of all division processes is identical, optimum thermodynamic selection will have always an identical probability without any special restrictions, i.e. the ratio of selections of cold and hot streams should be equal. These facts have been proved by examinations [Error! Reference source not found.].
Experiments
The analysis of industrial cyclone devices "NIIOGaz" type 15–D´1YP by calculating various entrance parameters according to the obtained mathematical model, Equation (10), showed that for a regime, which its temperature has not exceeded its boiling point, just 3-12 macroscopic elementary vortexes of "solid-state" character are needed.
Initial data of the cyclones "NIIOGaz" type 15–D´1YP is represented in Table 1.
Table 1. Initial data of the cyclones "NIIOGaz" type 15–D´1YP
|
D |
300 |
400 |
500 |
600 |
1400 |
|
Q |
1000 |
1800 |
2800 |
4100 |
22200 |
|
h*b |
206´86 |
274´114 |
340´140 |
406´166 |
934´374 |
|
D1 |
172 |
230 |
290 |
350 |
830 |
In the table above: D = diameter (mm), Q = volume expense (m³/h), h*b = the overall sizes of rectangular inlet duct (mm), and D1 = the diameter of exhaust duct (mm).
All calculation data on the cyclones "NIIOGaz" type 15–D´1YP are represented in Table 2:
Table 2. Calculation data on the cyclones "NIIOGaz" type 15–D´1YP
|
D(mm) |
300 |
400 |
500 |
600 |
1400 |
|
Q (m3/s) |
0,28 |
0,50 |
0,78 |
1,14 |
6,17 |
|
Gc(kg/s) |
0,60 |
1,08 |
1,68 |
2,46 |
13,33 |
|
υc (m/s) |
15,68 |
16,01 |
16,34 |
16,90 |
17,68 |
|
N |
12 |
9 |
7 |
6 |
3 |
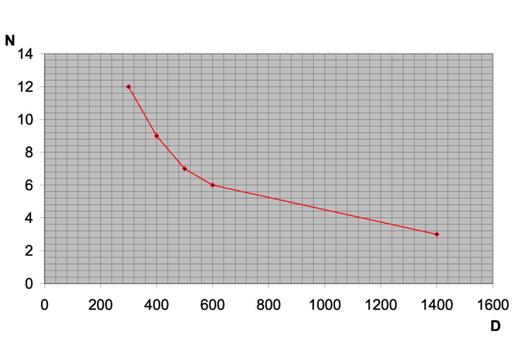
Figure 2. Changes of the number of macroscopic vortexes as compared to diameter of vortex tube for the (calculation) devices
This analysis shows that in order to maintain required effect without exceeding boiling point, we just need to have kept a thin wall layer in dependent vortex of solid object. Such a state regarding solid object in the region of vortex tube in the experimental work [5] has been considered based on high-speed filming.
In this work, maximal temperature difference on the exits of the vortex tube was about 60-70 degrees at the drop of pressure.
The dependence of a change in the linear speed on the portion of flow (processing experimental data) is represented in Table 3.
Table 3. The dependence of a change in the linear speed on the portion of flow (processing experimental data)
|
M |
0.98 |
0.92 |
0.86 |
0.80 |
0.74 |
0.67 |
0.60 |
|
Υ |
43.80 |
43.51 |
43.29 |
43.10 |
42.90 |
42.70 |
42.52 |
|
M |
0.41 |
0.31 |
0.23 |
0.17 |
0.15 |
0.12 |
|
|
Υ |
42.39 |
42.53 |
42.72 |
43.01 |
43.14 |
43.51 |
|
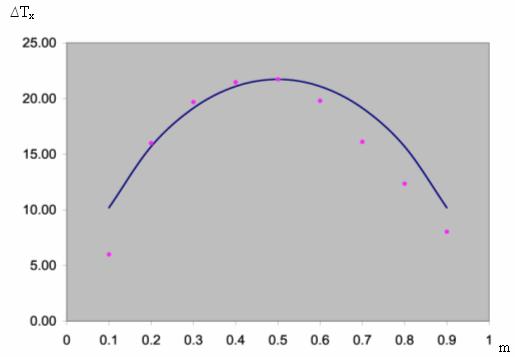
Figure 3. Comparison of the computational data with experimental data Calculation- Experiment (T = 293 K, G = 0,0032 kg/s, P = 168 КPа)
To analyze the mentioned method, experimental data of PhD thesis of doctorate student of Moscow State University of Engineering, M.A. Terekhov (2004), which was done under supervision of Professor O.A. Troshkin, were used [6].
Researches were done on a Ranque tube with separable box’s diameter of D=18mm and length of L = 125 mm. The experimental stand was equipped by the modern measurement and control set of equipments and automation equipments and advanced integral software programs.
Of experimental data, all regime parameters, which are used in Equation (10), except the number of macroscopic elementary dependent vortex, are clear in the package N. Their number was calculated 16 with general thickness of 2rN=0.11mm.
For comparison it should be noted that in this experiment there are h/2r=513 dependent elementary macroscopic layer in the opening of entrance tube.
Results and Discussions
During processing of experimental data with various ratios of products it has been noticed that multiplication of υbN in Equation (10) changes unnoticeably by change of selection of product in the selection region of m=0.5. According to this feature, thermodynamic method of the analysis of the vortex equipments was formulated, and following results were obtained accordingly.
On the basis of regime and structural parameters of vortex tube, the number of elementary macroscopic vortex for the regime of vortex tube N without exceeding of temperature from boiling point was calculated:
|
|
|
The analysis of the received result was carried out. There should be enough macroscopic vortexes so that the increase of vortex’s width (b) when the stream enters the vortex tube, does not lead to decrease of wave to N<1.
On the opposite, macroscopic vortex will transform to a microscopic state, which is the state of non–formation of stream’s cooling effect. To avoid this state, we may increase N against what we did at first and change the regime and structural parameters of device.
Recommended radius of selection of hot stream with theoretical justification in m=0.5:
|
|
|
We can estimate ideal of stream for macroscopic state by using information entropy of Shannon for two streams at the state of m=0.5:
|
|
|
Real efficiency of cooling
could be estimated. For an analyzed vortex tube this size equals to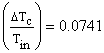 . Hence,
the coefficient of thermodynamic positive function will read: 0.0741/0.693= 0.107.
. Hence,
the coefficient of thermodynamic positive function will read: 0.0741/0.693= 0.107.
As seen, the approach of thermodynamic calculation can be applied for the Ranque vortex tube and other separator (dividing) systems [7].
Conclusion
The separation of a gas steam delivered to a tube, through a tangential nozzle into streams with different stagnation temperatures, is a phenomenon that has not yet been fully investigated.
Also confirmed that at invariable (constant) physical properties of environment cannot reverse the vortex effect, i.e. heating on axial and cooling on the peripheral layers is impossible. As well as offered the method of thermodynamic calculation of the effect of Rank, based features of the mode without overheating the input stream.
References
4. Martynov A.V., Brodyanskii V.M, What Is a Vortex Pipe?, Energy,. Moscow, 1976.
5. Gutsol A., The Ranque effect, Journal of Advances in Physical Sciences, 1997, 40(6), p. 639-58.
Symbols
с – Velocity of light in vacuum, с =2.998×108m/s
Fm – Inertial force in a macro cell, N
ћ – Planck's constant, ћ = 1.055×10-34J.s
k – Boltzma's constant, k = 1.381×10-23 J/K
m – Weight of a macro cell, kg
M – Molecular weight, kg/kmol
P – Pressure, N/m2
Ri – Radius of a current whirlwind, m
r – Macro cell radius, m
Т – Absolute temperature, K
Dt – The minimum macroscopical time scale, s
ρ – Density, kg/m3
ω – Frequency (angular speed), 1/s
D – Diameter of a vortex tube, m
L – Length, m
m – Relative (dimensionless) share of cold stream
Q – The volume expense, m3/s
υ – Linear speed, m/s
V – Whirlwind volume, m3
Subscripts
c – Cooled stream