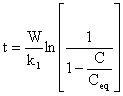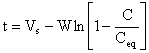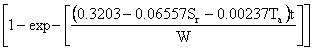Mathematical Model of Sorption Kinetics of Crude Oil by Rubber Particles from Scrap Tyres
Felix Aibuedefe AISIEN1,*, Robert Oboigbaotor EBEWELE1, Fredrick Kofi HYMORE2
1 Department of Chemical Engineering, University of Benin, Benin City, Nigeria
2 Department of Chemical Engineering, Covenant University, Ota, Nigeria
E-mail: afaisien2002@yahoo.com
* Corresponding author: Phone: +23408025343897
Received: 26 September 2011 / Accepted: 3 May 2011 / Published: 24 June 2011
Abstract
This paper present an insight into how rubber particles from scrap tyres can be utilized to clean up oil spillages as well as how the process of sorption of crude oil by rubber particles can be stimulated based on sorption kinetics. Crude oil sorption tests using recycled rubber particles (a model absorbent) were designed for investigating crude oil concentration profiles. The model based on a linear driving force (LDF) was developed using a set of experimental data and multiple regression analysis. The crude oil sorption performance tests were conducted under various operating conditions by varying parameters such as rubber particle size and absorption temperature. The predictive capacity of the kinetic model was evaluated under conditions significantly different from those that have already been measured. The experimental results obtained previously were correlated with the first order sorption kinetics model developed. The results showed that the first order kinetics model accurately correlate the experimental data generated. Also, satisfactory results were obtained from simulation of other operating conditions; hence the crude oil sorption kinetics is first order.
Keywords
Sorption Kinetics; Linear Model; Rubber Particles; Prediction; Simulation; Crude Oil.
Introduction
Recently in Nigeria, there has been increasing environmental awareness on the adverse effects of crude oil spillage on the environment especially among oil producing communities in the Niger Delta area. The environmental impact/hazard of crude oil spillage include: impeded reproduction of aquatic life, destruction of fishing grounds, destruction of vegetation and loss of soil fertility, reduced marine activities such as fishing and navigation and contamination of surface and underground water [1-2].
Several methods of remediation have been used in the past such as spraying of aqueous slurry of expanded graphite and chalk, burning of oil with wicking agents, disposing of oil with detergent, applying floating barriers or booms, using of polymeric foams and other absorbents such as recycled rubber and enhanced biodegradation [1-5]. However, the use of absorbents provided they are environmentally friendly, easily recoverable and of low cost has proved to be one the fastest way of combating oil spillage on the environment [6, 7]. Aisien et al. [1, 2] reported that recycled rubber from scrap tyres is very efficient for crude oil sorption. They stated that crude oil uptake by rubber particle is a combination of both absorption and adsorption and since absorption is a volumetric phenomenon and adsorption is a surface phenomenon, the uptake of crude oil is mostly due to absorption and to a considerably small extent due to adsorption. Also, they reported that rubber particles from scrap tyres absorbed 2.2 to 5.7 times its own weight depending on the sorption temperature and rubber particle size. Aisien et al. [1, 2] also reported that in a typical oil sorption process the uptake of oil by rubber was more controlled by a combination of kinetics and equilibrium. The success achieved in the clean-up of crude oil spill using rubber particles has necessitated this further investigation involving the development of a sorption kinetics model for predicting crude oil uptake using rubber particles. According to Tu et al. [8], the essence of model(s) is to facilitate the forecasting of process dynamics under different operating conditions, and conserves a great deal of effort, time and finance that would have been involved in planning and design. In this study, mathematical model will be developed using experimental data from Aisien et al. [1] and multiple regression analysis. experimental data will provide the necessary feedback for verification of the predictive capacity of the model. This research takes into consideration the concentration of crude oil uptake as a function of rubber particle size, sorption temperature, equilibrium sorption time and rubber particle weight. The simulation of crude oil sorption system was carried out to predict other different operating conditions outside the experimental ones. The kinetics of crude oil sorption was determined by direct measurement of the weight of rubber particle uptake (absorption) of crude oil as a function of other variables stated above [1].
The objectives of this research included: developing kinetic models (linear and quadratic), evaluating the predictive capacities of the models, simulation of crude oil absorption.
Material and Method
The sorption kinetics of crude oil by rubber particles is essentially based on the rate of the sorption system. It is quite obvious that for the crude oil sorption system the driving force is the concentration gradient of oil in the bulk solution and in the rubber particles. However, the rate strongly depends on the driving force, and in this case the diffusion process is the mechanism by which the oil is driven from the bulk solution into the rubber particles due to the presence of concentration gradient. Hence, it is assumed that linear driving force for the sorption of crude oil at any time t is the difference in concentration between the equilibrium and the bulk liquid time t. [9]
Rate of sorption of crude oil by rubber particles is given as:
|
dC/dt=k1(Ceq-C) |
(1) |
where C = Absorbed crude oil concentration at time t (g/g), Ceq = Absorbed crude oil concentration at equilibrium (g/g), that is mass transfer equilibrium and k = Mass transfer constant (min-1).
The weight of rubber, W is an important parameter in crude oil absorption model. This will enable accurate prediction of the quantity of rubber required for a given cleanup. However, it is independent on the concentration of the crude oil (C) and time (t), hence W is a non dimensionless constant. Thus, equation 1 becomes:
|
W(dC/dt)=k1(Ceq-C) |
(2) |
Integrating and rearrangement of equation (2) gives:
|
ln[Ceq/(Ceq-C)]=k1t/W |
(3) |
Solving equation (3) for C yields,
|
|
(4) |
Rearranging equation (4)
|
|
(5) |
Equation (5) is a modified first order sorption kinetics that is applicable to crude oil sorption by rubber particles.
Determination of Model Parameters
The use of the model to predict the absorption as a function particle size of rubber and temperature of absorption will require the variation of the mass transfer equilibrium, Ceq and the mass transfer constant, k as a function of these same parameters.
From the experimental data reported by Aisien et al. [1], the following correlation was tested to predict the mass transfer equilibrium, Ceq as a function of sorption temperature, Ta (in oC) and rubber particle size, Sr (in mm):
|
Ceq (Sr, Ta) = ao + a1Sr + a2Ta + a3SrTa +...+ anSnTn |
(6) |
where ao, a1, a2, and a3 are numerical constants which can be estimated by multiple regression analysis.
Set of 36 Ceq values which were obtained from experimental results as reported by Aisien et al. [1] was used in the search equation 6. The regression analysis showed that ao, a1, a2, were 6.1764, -1.446 and -0.002786 respectively. Hence the equation becomes:
|
Ceq (Sr, Ta) = 6.1764 -1.446Sr - 0.002786Ta |
(7) |
Equation (7) was used to calculate mass transfer equilibrium Ceq,. The calculated Ceq, correlated favourably with the measured Ceq as reported by Aisien et al. [1]. Also, similar trend was observed that it, Ceq decreases with decrease in rubber particle size (S_r) and increase in sorption temperature (T_a). The accuracy of this correlation was about 92 percent.
Additional terms in eq. (7) did not make any significant difference to the accuracy of the predictions of the mass transfer equilibrium. The substitution of eq. (7) into the derived model equations enabled the determination of the only unknown model parameter, which is the mass transfer constant, k.
The mass transfer constant, k can be calculated from the appropriate plots of the rearranged model equation 5. From eq. (5) k, is obtained from the slope of the plot
|
|
(8) |
This is illustrated in Figure 1 using rubber particle size of 0.60mm and sorption temperature of 30oC. The high correlation coefficients, (R2 > 0.99) testify to this by the linear model.

Figure 1. Variation absorption time with W*In[1-(C/Ceq)] for linear model
With the generation of the mass transfer constant, k for the different sorption temperatures and rubber particle sizes, a correlation similar to eq. (7) was obtained by using the least square method. This gave the mass transfer constant, k as a function of sorption temperature and rubber particle size.
Based on linear driving force model, k correlation is
|
k (Sr,Ta) = 0.3203 - 0.06557Sr - 0.00237Ta |
(9) |
This gives a mass transfer constant which decreases with rubber particle size (S_r) and sorption temperature (Ta).
Substitution of equations (7) and (9) into eq. (4) will enable the evaluation of the concentration of oil absorbed, C as a function of the most relevant parameters such as sorption temperature, Ta particle size of rubber, Sr weight of rubber, W and time for sorption, t.
The linear driving force model,
|
C( t, Sr, Ta, W) = (6.1764-1.446Sr- - 0.002786Ta) |
(10) |
Results and Discussion
Comparison of the LDF model data with measured data
Equations (10) was used of generate the concentration - time data for the LDF model. The calculated concentration - time data were compared with the experimental results (measured data). Figure 2 shows the comparison of the measured concentration data with calculated concentration data for different particle sizes of rubber and sorption temperatures. It can be seen that the calculated concentration-time data conformed to experimentally obtained concentration-time data. As a result, the predictions of the model were very satisfactory.
Figures 3 to 5 show the comparison of the experimental obtained concentration - time data with concentration - time data based on LDF model prediction. These Figures also support the fact that the predicted concentration-time data compared favorably with the experimental concentration-time data. In all cases, it can be seen that the experimental/measured data and the predicted/calculated data for the concentration of absorbed crude oil gave an excellent agreement. However, the good performance of the model show that the correlation used for the predictions of the basic parameters is still valid.
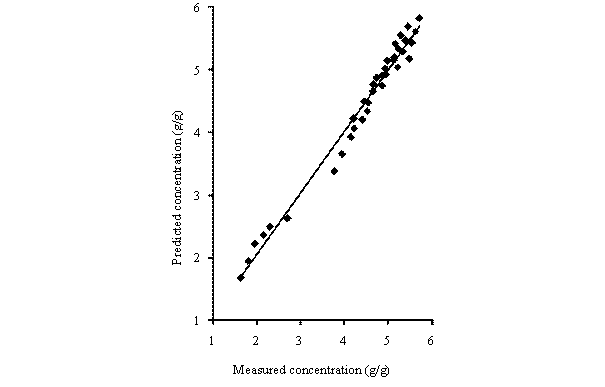
Figure 2. Comparison of the measured concentration with model predictions at different rubber particle sizes and temperatures
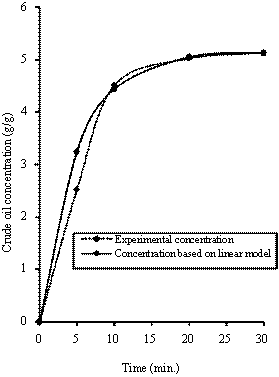
Figure 3. Comparison of the experimental concentration with concentration based model predictions [278K, 0.425mm]
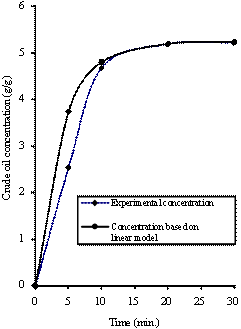
Figure 4. Comparison of the experimental concentration with concentration based model predictions [288K, 0.300mm]
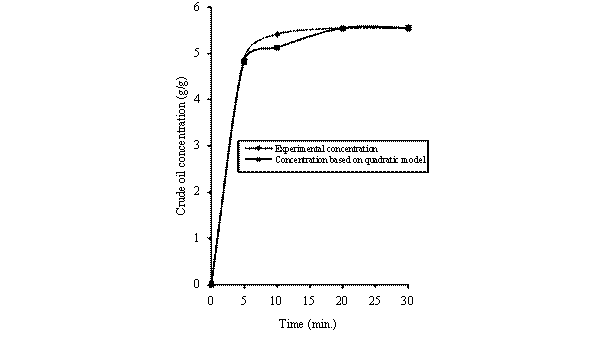
Figure 5. Comparison of the experimental concentration with concentration based model predictions [293K, 0.600mm]
Simulation of Concentration - Time Data using Linear Model
The LDF model was employed in the simulation of concentration - time data for different rubber particle sizes and for different sorption temperatures outside the experimental conditions reported earlier by Aisien et al. [1].
Figure 6 shows the concentration - time profile for different rubber particle sizes (0.075mm, 0.212mm, 0.50mm, 2.00mm, 3.35mm and 4.00mm) at 15°C. The observed trend in Figures 6 is similar to that obtained experimentally as reported by Aisien et al. 2003 and 2006. The trend shows a rapid, initial increase in sorption, followed by a decrease until an asymptotic value is reached at equilibrium crude oil sorption. Figure 6 shows the smaller the rubber particle size, the faster and better was the crude oil sorption. This indicates that the uptake of crude oil was more controlled by combination of kinetics and equilibrium as earlier stated by Aisien et al. [1, 2], and this is apparent from the results presented in Figure 6. It can also be seen that the saturated uptake concentration is approximately proportional to the reciprocal of the particle size of rubber. This is so because the rate of uptake is dependent on the specific surface area of the rubber particles.

Figure 6. Variation of crude oil absorption at 298K with rubber particle size
Figures 7 shows the concentration - time profile for different sorption temperatures (7°C, 12°C, 18°C, 25oC, 35°C and 50°C) using 0.60mm rubber particle size.
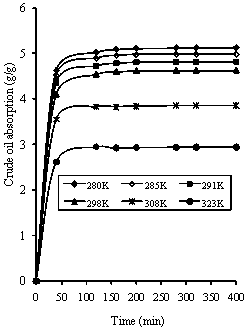
Figure 7. Variation of crude oil absorption a with temperature (0.600mm rubber particle size)
The observed profile in Figures 7 is also similar to that obtained experimentally as reported by Aisien et al. [1, 2]. The results in Figure 7 substantiate the fact that crude oil sorption is an exothermic process and is therefore not enhanced by an increase in temperature. The uptake of crude oil decreases with increasing temperature. This statement has been clearly explained in the earlier report by Aisien et al. [2]. In conclusion, the results in Figures 6 and 7 show the consistency of the LDF model and the accuracy of predictions was about 68 percent. The smaller the particle size of rubber the larger the concentration of oil absorbed. Similarly, the lower the sorption temperature, the higher the concentration of oil absorbed. However, the simulation at different sorption temperatures was better than for different rubber particle sizes using the first order kinetics model obtained from set of experimental data and multiple regression analysis.
Conclusion(s)
The following conclusions can be drawn from this study:
· The model based on a linear driving force (LDF) was developed using a set of experimental data and multiple regression analysis.
· The crude oil sorption kinetics is a first order.
· The accuracy of the model predictions is about 68 percent and the model predictions were consistent with experimental results earlier obtained.
· The simulation shows the expected trends of crude oil absorption with respect to rubber particle size and sorption temperature.
References
3. Aisien F.A., Potential applications of recycled rubber from scrap tyres Ph.D thesis, Department of Chemical Engineering, University of Benin, Benin City, Nigeria, 2003.
4. Lewicke C.K., Cleansing Up Oil Spills Isn’t Simple, Environmental Science and Technology, 1973, 7(39), p. 400-410.
5. Imevbore A.M.A., Ekundayo J.A., Effect Of crude Oil Effluent Discharge on the Water Quality and Biological Production in the Niger-Delta, Nigeria. Final Report, Shell Petroleum Development Company, Nig. Ltd., Lagos, 1987, p. 197-260.
7. Labelle R.P., Galt J.A., Tennyson E.T., Mcgrattan K.B., The 1993 oil spill of Tampa Bay, a scenario for burning; Spill Sci. Technol. Bull., 1994, 1(1), 5-9.
8. Tu S.C., Ravindran V., Den W., Pirbazari M., Predictive membrane transport model for nanofiltration processes in water treatment AIChE 2001, 2001, 47(6), p. 3-4.