ParCop with New Capabilities and Efficient Scheduling Policies

 

Nidal Aabid AL-DMOUR, Mohammad Suleiman SARAIREH*

 

Computer Engineering Department, Faculty of Engineering, Mutah University, B.O.Box (7), Mutah 61710, Jordan

E-mails: nidal@mutah.edu.jo, m_srayreh@mutah.edu.jo

*Corresponding author E-mail: m_srayreh@mutah.edu.jo

 

Received: 5 March 2011 / Accepted: 14 March 2011 / Published: 24 June 2011

 

 

Abstract

The increase in PCs' capabilities and communication bandwidth over the last decade has made distributed computing a more practical idea for solving computational problems. We have developed a decentralized P2P system called ParCop (Parallel Cooperation). ParCop enables each peer in a P2P network to view the rest of the network as a supercomputer, by running ParCop system software on the machine as a daemon service. ParCop allows participants to execute different applications on shared resources owned by other participants. In this paper, we present the new capabilities of ParCop system: efficient resource discovery by using the Blackboard Resource Discovery Mechanism (BRDM), adaptation in dynamic networks, effective data caching, efficient scaling and the provision of a secure environment. We also present three scheduling policies that allow peers in ParCop environment to take scheduling decisions based on the information coming from the peers in the network. The use of these scheduling policies minimizes the processing time of applications in ParCop, improves the ability of dealing with peers which have different capabilities and requirements, and achieves efficient load balancing.

 

Keywords

Peer-to-Peer; ParCop; Decentralized; BRDM; Scheduling policies; Resource discovery; Speedup; Fault tolerance.

 

 

Introduction

 

The increase in PCs' capabilities and communication bandwidth over the last decade has made distributed computing a more practical idea for solving computational problems. P2P systems can be used to create a distributed computing environment and can exploit the idle CPU cycles of tens of thousands of networked computers to work together on a particularly process-intensive problem that previously had to be done on supercomputers. Not all applications are suitable for distributed computing using the P2P computing model, however, loosely coupled tasks with high computation to communication ratio are the most appropriate applications. These tasks can tolerate the constantly changing availability of peers and the high latency and low bandwidth connections of some peers.

Many peer to peer protocols have been developed in the last ten years. They can be grouped into few architectural models, taking into account: the dispersion of information and the logical organisation of peers [1]. We have developed a decentralized P2P system called ParCop [2]. ParCop enables each peer in a network to view the rest of the network as a supercomputer, by running ParCop system software on the machine as a daemon service. ParCop allows participants to execute different applications on shared resources owned by other participants. A peer in ParCop performs four simultaneous operations: the use of another peer’s resources; the sharing of its resources with other peers; the forwarding of queries to neighbours; and the caching of computational results.

In this paper, we present the new capabilities of ParCop system: efficient resource discovery by using the Blackboard Resource Discovery Mechanism (BRDM), adaptation in dynamic networks, effective data caching, efficient scaling, and the provision of a secure environment [3, 4]. We also present three scheduling policies that allow peers in ParCop environment to take scheduling decisions based on the information coming from the peers in the network. The use of these scheduling policies in ParCop minimizes the processing time of the tasks, improves the ability of dealing with peers that have different capabilities and requirements, and achieves efficient load balancing.

This paper is divided into six sections: related work; ParCop overview; ParCop’s new capabilities; the proposed scheduling policies; performance evaluation; and conclusions.

 

Related Work

The Berkeley Open Infrastructure Networking Computing (BOINC) system is a software platform for distributed computing using volunteer computer resources [5,6]. Participants can join one or more of the BOINC projects by registering for an account at a project site, then downloading and running the BOINC client. Many different projects can use BOINC and each project has is own servers and databases. Projects can share resources with each other. When a project has no work or it is down, the resources of its participants will not be wasted and they will be divided among other projects. BOINC systems follow the client/server model. BOINC solve the problem of single point of failure by having several servers and for each project.

KOALA [7] and Gridway [8] are examples of large scale Grids that consist of multiple sites usually use hierarchical metaschedulers. In these projects, each site has its own scheduler for resource coordination and jobs accepting from local nodes. The site scheduler acts as a metascheduler which polls the schedulers from other sites in the Grid for available resources and requests job execution. Thus, the metascheduler suffers from a bottleneck problem.

In order to achieve better fault-tolerance and scalability, decentralized Grid schedulers was proposed. In Zorilla [9], a node can directly submit jobs to another node in the overlay. The resource discovery is achieved by flooding the overlay with search messages. However, this approach has a major drawback that is the generation of a high number of messages.

 

 

Materials and Methods

 

ParCop is a decentralized P2P system in which there is no central point of control; data and tasks are mobilized and flow between the computational resources (peers) without going through a central server. ParCop allows a group of peers to speed up long running tasks by breaking the tasks down and distributing the work between each other.

Obviously, not all applications are supported by ParCop. ParCop supports applications where the problem can be divided into small tasks and people can easily participate in the computation by installing ParCop software on their machines. In general, these applications must have a very high computation versus communication ratio. For example, finding whether a number is prime or not is a very intensive computational problem, especially if the number is very large (i.e. the number is greater than or equal 106). A message is encapsulated with the results of this computation, which says whether or not this number is a prime. It takes just a few seconds to deliver the results for a problem that takes hours to be solved.

ParCop supports the master/worker style of application. A peer in ParCop can become a Pmaster or a Pworker, but not both at the same time. If the peer is a Pmaster, it distributes the tasks, collects the computed results, and returns the results to the user. If the peer is a Pworker, it receives the task from the Pmaster, and performs the computation and returns the results to the Pmaster. The following steps explain how the Pmaster finds idle peers:

·        Each peer P is initially connected to a number of peers.

·        Each peer becomes active when it receives tasks from the user, who develops application A and interfaces it with P. P now is known as Pmaster.

·        Once the Pmaster receives the tasks from the user, it starts sending query messages to its neighbours. The Pmaster sends a MasterQuery message to a ratio of its neighbours from the routing table and this ratio is decreasing as the MasterQuery message is forwarded from one node to another as the TTL is decreasing (based on BRDM approach for forwarding the query messages mentioned in [2]).

·          The peer P which receives the MasterQuery message will check whether it has been allocated for another Pmaster or not by accessing the blackboard it maintains. If it has not, a WorkerReply message will be passed back to the Pmaster through each node that forwarded the MasterQuery message, to inform the Pmaster of the worker's readiness to receive the task.

·          The Pmaster chooses the workers which run the task based on a scheduling policy and starts sending the tasks and the input data to each Pworker. Then, the Pmaster waits for the workers to finish executing the tasks. The Pmaster collects all the results and returns them to the user.

Further in the paper, we present the improvements that we have made on ParCop.

 

Efficient Recourse Discovery

The method of finding volunteers to run a user application over the ParCop environment is based on the BRDM. The BRDM is a decentralized mechanism and in [3,4] we showed that BRDM is scalable and can find resources even in a network with ten thousands nodes. The BRDM can be used for file sharing [3] and distributed computing [4]. BRDM nodes forward queries to neighbours that have answers. If a node cannot answer a query, it forwards the query to a subset of its neighbours which are recommended to have the requested resource, rather than by selecting neighbours at random.

To use BRMD for distributed computing an arbitrary label called “CPU object” has been introduced in [4] which represents the CPU cycles of a peer and indicates to other peers in the system that it is willing to donate its computing resources. The blackboard that each node maintains in a P2P network will contain “CPU objects” of the peers in the network. The experiments on BRDM for distributed computing in [4] show that the BRDM approach for finding idle peers to run the tasks achieves a high success rate for large networks with the size up to 10,000 peers. ParCop has been developed to take advantage of the DRM algorithm. Each peer in ParCop maintains a blackboard that stores CPU Objects which represent the CPU computing resources of the peers willing to be part of a distributed computation. The “CPU object” has attributes that represent the capabilities of a peer.

            Therefore, the WorkerReply message encapsulates the “CPU Object” which describes Pworker attributes and returns it to the Pmaster as well as enters it at the blackboards of the intermediate peers that forwarded the MasterQuery message. The Pmaster receives the WorkerReply message from the Pworker and saves its address in the table of workers. If the TTL of the MasterQuery messages is not expired, the Pworker will forward it to:

·       a ratio of its neighbours or,

·       to a list of recommended peers if its blackboard contains “CPU objects” of other peers in the network.

 

Fault Tolerance

ParCop is capable of dealing with machine failures by performing regular checks between Pmaster and the workers to find out if they are still alive. If a Pworker leaves the computation or becomes unreachable, the Pmaster will send MasterQuery messages to its neighbours in order to send the unfinished task to one of them so that the overall computed result is not affected.

ParCop is also fault tolerant if the Pmaster fails and becomes unavailable for some reason. The workers will carry on the computation even if the Pmaster is no longer connected to them. The tasks that the user sent to the workers are assigned a tuple <taskID, IP address of Pmaster >, the Pworker caches the computed result if the Pmaster becomes unavailable, and the results are encrypted and the task ID saved with the name “taskID_IP”. Once the Pmaster returns online, the computed results can be easily recovered by the user from the tasks_ IDs.

The user must send these task IDs to the ParCop daemon, which in turn sends a query message to the workers requesting the computational results. A Pworker which has cached the computed results will search its local repository to find the cached results. The Pworker uses the IP address and the task ID sent by the Pmaster as identification in order to send the results of the tasks sent by the requested Pmaster. To achieve an efficient fault tolerance with ParCop, the cached results are replicated among the Pworker immediate neighbours in case the Pworker fails after the Pmaster is back on line.

 

Scalability, Security and Adaptive Parallelism

ParCop uses the BRDM for finding workers. Based on the experiments in [2], ParCop can work in an environment of 10,000 peers and is capable of finding enough volunteers to run the application. ParCop is scalable and does not require a centralized server, or any super-peers to arrange the execution of the tasks among the peers or to perform resource discovery.

The tasks that the scheduler sends to the workers are digitally signed with the “SHAwithDSA” algorithm [10], which is provided by Java. SHAwithDSA contains a method which hashes the tasks using the SHA algorithm and then encrypts the computed results by using the DSA (Digital Signature Algorithm). A Pworker first checks the signature of the received tasks and if they have been tampered with, they will not be run. The computational results are also encrypted.

The set of workers executing the tasks may grow or shrink. Even if a computation ends on the same number of workers, they need not be the same workers on which it started. ParCop reallocates tasks as necessary during the computation. The user can send an unlimited number of tasks to the ParCop daemon and they will be distributed among the workers. If the number of workers is smaller than the number of tasks, the scheduler will distribute some of the tasks among the workers which have already been found, and will continue to send further messages.

 

The Proposed Scheduling Policies

Each peer in ParCop has a scheduler which receives from the user the tasks that compose the application, chooses which Pworker runs each task, submits the tasks for executing, and monitors their progress. To perform an efficient scheduling, the scheduler requires adequate information about the capabilities of the Pworker. We have defined three scheduling policies to be used in ParCop.

Rr stands for resource requirement that a user wants for a Pworker to have in order to run a task where:

 

 

Metric Ψ can be defined as shown in Equation 1 where the weightings represent the importance of each attribute of the CPU object with respect to each other (w1 + w2 + w3 + w4 = 1):

(1)

 

For each MasterQuery message sent by the Pmaster, a set of workers is found and returned to the scheduler. The scheduler then calculates Ψ for each Pworker and arranges the workers in ascending order and sends the tasks to them. The tasks that the user sends to the scheduler are entered in a task queue which sends them to the workers in the same order that they have been received from the user.

·        The second scheduling policy: If the user does not specify the minimum requirements of the workers which will run the tasks, the second scheduling policy will be used in ParCop. It is based on completion efficiency. The completion efficiency is another attribute that is attached to the “CPU object” and it has a value between 0 and 1. The completion efficiency is allocated to a worker after it has finished running a task from the Pmaster. After the Pmaster has received the results from all of the workers, it calculates the completion efficiency  for each worker by using Equation 2. A peer might have been used several times so the average of  will be calculated and stored in the peer’s blackboard (each peer in ParCop has blackboard). Once the scheduler receives the list of peers found by the MasterQuery message, the scheduler will arrange the peers according to their completion efficiencies and those with lower values for  will be given higher priority for running the tasks.

(2)

·        The third scheduling policy: The MasterQuery message might find peers that are willing to be part of the computation but have never been used before and have never been given completion efficiency. In such cases, the scheduler will arrange them based on their processing speed.

 

 

Results and Discussions

 

The scheduling policies used by ParCop were described. There were three scheduling policies:

The first scheduling policy is based on allowing the user to specify the minimum requirements for the workers which will run the tasks. This policy was tested in [2], where it was shown that the BRDM algorithm that ParCop uses was efficient in terms of finding more workers than other search algorithms.

The second scheduling policy is based on assigning tasks to workers with minimum completion efficiency. We refer to this scheduling policy as MCE.

The third scheduling policy is based on assigning tasks to workers with maximum processing speed and arranging the processors in descending order. A worker processing speed is an attribute attached to the “CPU object”. We refer to this scheduling policy as MPS.

 

Performance Evaluation of MCE and MPC

Several experiments were conducted which follow the master/worker paradigm in order to assess the performance of our system. A 22-processor cluster was used to implement the experiments. These machines were connected to the network via a 100 Mbps switch as shown in Table 1.

 

Table 1. The details of the hardware configurations of the machines used for measuring the performance of ParCop

Processor

OS

RAM

16Ultra-Sparc 500 MHz

Solaris 9 08/03

512 MB

6Ultra-Sparc 350 MHz

Solaris 9 08/03

512 MB

 

The applications we experimented with are: Mersenne Prime Number search [11]; and Brute Force Attack [12]. Each of these applications has the required high computation to communication ratio. ParCop software was installed on each of the 22 processors and each peer was connected to 5 other peers. We randomly chose one of these machines to send the application to. The chosen machine became a Pmaster and sent the tasks to the workers. The speedup is measured using Equation 3, where τone is the time required to perform the computation on one Pworker and τmultiple is the time required to perform the same computation on multiple workers. τmultiple is the sum of times required for: the query manager to find the workers; the tasks and the input parameters to be sent to the workers; the execution and running of the tasks; and the results to be received from the workers and returned to the developer application.

D = τone/τmultiple

(3)

We compare both MCE and MPS with tasks randomly assigned (RA) to the workers in ParCop (i.e. without any scheduling policy). We repeated our experiments several times. The results shown in this chapter are the average values of measurements obtained from multiple runs.

 

Mersenne Prime Number

A Mersenne Prime [11] is a prime number of the form 2p minus 1, where both the number and the exponent p are primes. The form 2p minus 1 is not always valid: in 1536, Hudalricus Regiuos showed that 211 minus 1 equals 2047 was not a prime (it is 23×89). Mersenne primes are found using the following Lucas-Lehmer Test [13]. The test says that for p odd, the Mersenne number 2p minus 1 is prime if and only if 2p minus 1 divides S(p-1), where  equals , and S(1) equals 4.

There are only 41 known Mersenne prime numbers. The 41st Mersenne prime number was found in May 2004; it took nearly a year and a half and tens of thousands of computers as part of the GIMPS project [11]. The search for Mersenne primes becomes more difficult with larger numbers. This kind of application is coarse-grained and has a high computation to communication ratio for large numbers [11].

We tested the Mersenne primality for all the numbers between 3000 and 4000. The range between 3000 and 4000 was broken into sub-ranges of equal sizes, based on the number of workers that the user required in order to run the application. However, ParCop is adaptively parallel and the number of workers that run the tasks could be smaller than the number of the tasks that the user sent to the ParCop daemon. The time is measured from the moment the Pmaster received the tasks to the moment that the user started to receive the results back from the Pmaster. The time taken for one Pworker to find the prime numbers was 7,317,828 milliseconds. The speedup from using more than one Pworker was measured using Equation 1 as shown in Table 2.

The speedup in finding the prime numbers using the ParCop infrastructure is shown in Figure 1. The speedup is calculated using Equation 3 by measuring the time spent to find the prime numbers between 3000 and 4000 using one processor. The range from 3000 to 4000 was divided into sub-ranges and one sub-range was allocated to each of the workers. Although the sub ranges were equally divided between the workers, the amount of the computation that each Pworker performed was not equally divided, because finding the primary numbers between the lower subranges (near to 3000) took longer than finding the prime numbers between higher subranges: the higher the number, the more computation was required to work out whether it was a prime. The difference in the amount of work that each Pworker performed is the reason why the speedup was not equal to the ideal situation. The scheduler at the Pmaster was not capable of detecting which range was intensively computed and which range was not. It is the responsibility of the user to equally divide a computational problem. However, the results show that a good speedup can be achieved by using MCE and MPS compared with RA.

Table 2. Experimental Results for Primality Test

No. of

Workers

MCE&MPS

RA

Ideal

Speedup

Time(ms)

Speedup

Time(ms)

Speedup

1

7464739

0.980319

7505676

0.974973

1

2

4527957

1.616143

4508510

1.623115

2

4

2478592

2.952413

2478138

2.952954

4

6

1732907

4.222863

2163748

3.382015

6

8

1312863

5.573946

2845284

2.571915

8

10

1051813

6.957347

1216368

6.01613

10

12

926265

7.900361

1166647

6.27253

12

14

826176

8.857469

1040595

7.03235

14

 

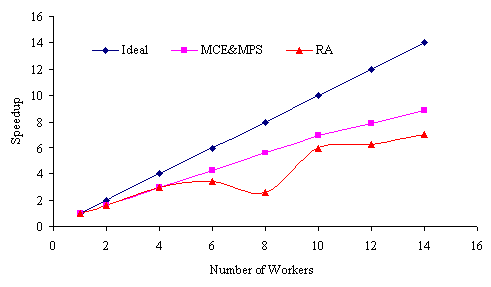
Figure 1. The speedup curve for primality test

Brute Force Attack

Brute force attack [12] is an example of a master/worker application in which the search for the solution can be divided between multiple machines. An example of brute force attack is factorizing. We have developed a Java application which factorizes a set of numbers.

The set contains 10000 numbers which, for the purpose of this experiment, are identical. We have chosen a random number for factorisation: 12299292. The reasons for selecting this number and doing 10000 copies of it are:

·      To make sure that each worker obtains the same amount of work and to maintain consistency in our sets of measurements;

·      To ensure the number was small enough for the experiment to conclude with a reasonable length of time.

The ten thousand copies of 12299292 were divided between the workers by the Pmaster, which then collected the results and returned them to the user. The speedup was measured using equation 3 and is shown in Table 3. The time required to factorize the set of numbers decreased as the number of workers increased. The speedup curve in Figure 2 shows that factorizing the set of numbers on workers was very close to the ideal situation, because the amount of work that the Pmaster handled to each worker was the same and took the same amount of computation. Again, MCE and MCP outperform RA.

 

Table 3. Experimental Results for Brute Force Factoring

No. of Workers

MCE & MPS

RA

Ideal

Speedup

Time(s)

Speedup

Time(s)

Speedup

1

2756304

0.9862

2756704

0.98606

1

2

1394748

1.94894

1384748

1.96301

2

4

698014

3.8943

869519

3.12619

4

6

467414

5.81557

467849

5.81016

6

8

353336

7.69318

439968

6.17835

8

10

285970

9.50547

353748

7.68422

10

12

238837

11.3813

297096

9.14949

12

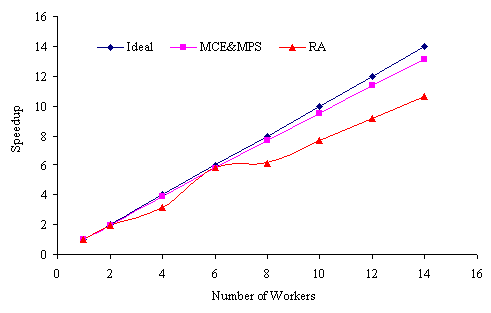
Figure 2. The speedup curve for factoring a set of ten thousands numbers over multiple workers

 

Fault Tolerance

In this section, we present some experiments designed to show that ParCop is fault tolerant. In these tests, we chose to run a simple factorization application. The developer application sent to the Pmaster three sets of tasks: 5, 10, and 15 tasks. For sake of comparison, the time required to run 5 tasks was the same time required to run 10, and 15 tasks respectively. When there were no failures, the time required to run each set of the tasks was 372914 milliseconds with MCE and MPS, and 464074 milliseconds with RA. We started to kill the workers two minutes after they had begun.

Figure 3 and Figure 4 show that MCE and MPS outperformed RA. The completion time for running the tasks after peer failures was shorter with MCE and MPS than with RA. Figure 5 shows that both MCE/MPS and RA exhibited the same performance because the number of tasks was equal to the number of processors with high processing speeds. In Table 1, the number of processors with high processing speed was 16 and one of them was used as a Pmaster. Therefore, when the MCE and MPS had been applied in ParCop and the peers failed, the unfinished tasks were rescheduled on the slow processors.

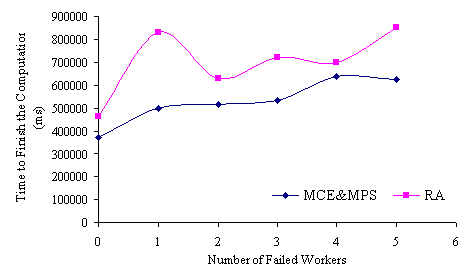
Figure 3. The time taken to finish the computation of five tasks when the workers were withdrawn from the computation

 

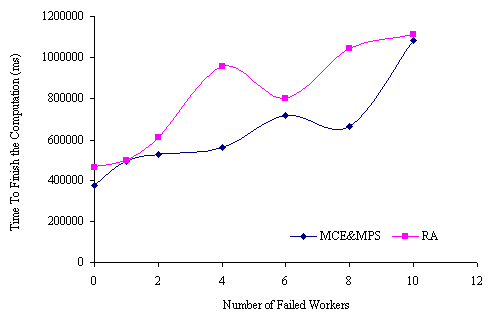
Figure 4. The time taken to finish the computation of ten tasks when the workers were withdrawn from the computation

 

In Figure 5 is shown that there was an increase in the completion time if 15 workers failed and the Pmaster needed to reschedule all the tasks. This is because, after 15 workers failed, only 6 peers remained to run the tasks (the experiment was performed with 22 processors), so some workers ran two or three tasks.

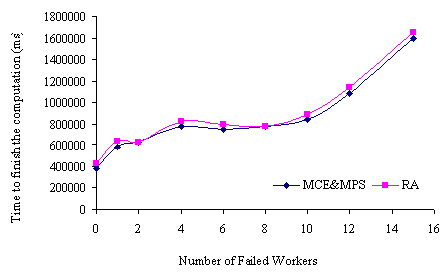
Figure 5. The time taken to finish the computation of fifteen tasks when the workers were withdrawn from the computation

 

 

Conclusions

 

We have developed ParCop, a decentralized P2P system, for executing independents tasks among peers. In this paper, we discussed the new capabilities of ParCop system: efficient resource discovery by using the Blackboard Resource Discovery Mechanism (BRDM), adaptation in dynamic networks, effective data caching, efficient scaling, and the provision of a secure environment. The BRDM approach for distributed computing lies at the heart of the ParCop implementation. With BRDM, ParCop is able to efficiently utilize the computational resources of the peers distributed across the network.

We presented three efficient scheduling policies which: minimize the processing time of applications in the system, improve the ability of dealing with peers which have different capabilities and requirements, and achieve efficient load balancing.

It was shown that the use of MCE and MPS scheduling allows for a better speedup to be achieved and minimizes the completion time of tasks over the ParCop environment.

ParCop was tested when the peers were withdrawn from the computation, and showed that it is fault tolerant for this section. For example, a computation using ParCop can start with multiple workers and finish with one Pworker.

 

 

References

 

1.             Amoretti M., A Framework for Evolutionary previous termPeer-to-Peernext term Overlay Schemes, European Workshops on the Applications of Evolutionary Computation (EvoWorkshops 2009), Tubingen, Germany, April 2009.

2.             Al-Dmour N., Teahan W.J., ParCop: A Decentralized Peer-to-Peer Computing System, The 3rd International Symposium on Parallel and Distributed Computing in association with HeteroPar'04, University College Cork, Ireland, July 2004.

3.             Al-Dmour N., Teahan W.J., The Blackboard Resource Discovery Mechanism for P2P Networks, The 16th IASTED International Conference on Parallel and Distributed Computing Systems (PDCS), MIT, Cambridge, MA, USA, November 2004.

4.             Al-Dmour N., Teahan W.J., The Blackboard Resource Discovery Mechanism for Distributed Computing over P2P Networks, The IASTED International Conference on Parallel and Distributed Computing and Networks (PDCN), Innsbruck, Austria, February 2005.

5.             Anderson D., Public Computing: Reconnecting People to Science, Conference on Shared Knowledge and the Web, Madrid, Spain, November 2003, p. 17-19.

6.             BOINC project, http://boinc.berkeley.edu/, Accessed January 2011.

7.             Mohamed H., Epema D., KOALA: A Co-Allocating Grid Scheduler.Concurrency and Computation, Practice and Experience, Wiley, 2008, 20(16), p. 1851-1876.

8.             Huedo E., Montero R.S., Llorente I., The Gridway Framework For Adaptive Scheduling And Execution On Grids. Scalable Computing, Practice and Experience SWPS, 2005, 6(3) p. 1-8.

9.              Drost N., van Nieuwpoort R.V., Bal H., Simple locality-aware coallocation in peer-to-peer supercomputing, In Proc. of the 6th Symposium on Cluster Computing and the Grid. IEEE, 2006, p. 8-14.

10.          “SHAwithDSA”, Java Cryptographic Architecture, http://jce.iaik.tugraz.at/products/ 01_jce/features/index.php, Accessed December 2004.

11.          GIMPS project, http://www.mersenne.org/prime.htm, Accessed January 2011.

12.          Brute force attack, http://en.wikipedia.org/wiki/Brute_force_attack, Accessed January 2011.

13.         Lucas-Lehmer Test, http://www.mersenne.org/math.htm, Accessed January 2011.