Adaptive Differential Evolution Approach for Constrained Economic Power Dispatch with Prohibited Operating Zones
Samir SAYAH and Abdellatif HAMOUDA
Department of
Electrical Engineering,
E-mails: samir_pg04@yahoo.fr, a_hamouda1@yahoo.fr
Abstract
Economic
power dispatch (
Keywords
Economic Power Dispatch; Differential Evolution; Power System Optimization; Prohibited Operating Zone.
Introduction
The conventional economic power dispatch (
The
In recent years, new optimization techniques based on the principles of natural evolution, and with the ability to solve extremely complex optimization problems, have been developed. These techniques, also known as evolutionary algorithms, search for the solution of optimization problems, using a simplified model of the evolution process found in nature [1]. Differential Evolution (DE) is one of these recently developed evolutionary computation techniques [2, 3]. Differential evolution improves a population of candidate solutions over several generations using the mutation, crossover and selection operators in order to reach an optimal solution. Differential evolution presents great convergence characteristics and requires few control parameters, which remain fixed throughout the optimization process and need minimum tuning [4].
In this paper, an adaptive differential evolution (ADE) based technique is presented and used to solve the economic dispatch problem, with non-convex, non-continuous, and non-linear cost functions. An application was performed on the 6-unit benchmark test system, with ramp rate limits and prohibited operating zones. The results obtained through ADE and those of the previous methods are compared. The outcome of the comparisons confirms the effectiveness of the proposed ADE approach in terms of solution quality, consistency and computation rapidity.
Basic Economic Power Dispatch Formulation
The
objective of
|
Minimize F(x) |
(1) |
|
Subject to: g(x) = 0 |
(2) |
|
Subject to: h(x) £ 0 |
(3) |
F(x) is the objective function; g(x) and h(x) are respectively the set of operation constraints. x is the vector of control and state variables.
Objective Function
The objective function for the ELD reflects the cost associated with generating power in the system. The objective function for the entire power system can then be written as the sum of the fuel cost model for each generator, a follows:
|
|
(4) |
where ng is the number of online generating units. Fi is the fuel cost function of the ith generator in ($/h), which is usually expressed as a quadratic polynomial:
|
|
(5) |
where Pi is the power of generator i. ai, bi and ci are the cost coefficients of generator i.
Power Balance Constraint
The power balance constraint reduces the power system to a basic principle of equilibrium between total system generation and total system loads. Equilibrium is only met when the total system generation equals the total system load PD plus system losses PL as it is shown in (6).
|
|
(6) |
The exact value of the system losses can only be determined by means of a power flow solution. The most popular approach for finding an approximate value of the losses is by way of Krons loss formula (7), which approximates the losses as a function of the output level of the system generators.
|
|
(7) |
Generator Operation Constraints
Generating units have lower and upper production limits, which are directly related to the design of the machine. These bounds can be defined as a pair of inequality constraints, as follows:
|
|
(8) |
where ![]() and
and ![]() are the minimum and
maximum generation of unit i, respectively.
are the minimum and
maximum generation of unit i, respectively.
Ramp Rate Limit Constraints
In
(1) if generation increases,
|
|
(9) |
(2) if generation decreases,
|
|
(10) |
where ![]() and
and ![]() are the current
and previous power output of unit i, respectively. URi and DRi
are the up and down ramp rate limit of the ith
generating unit (in MW/h), respectively.
are the current
and previous power output of unit i, respectively. URi and DRi
are the up and down ramp rate limit of the ith
generating unit (in MW/h), respectively.
Prohibited Operating Zones
Prohibited operating zones in the input-output curve of generator are due to steam valve operation or vibration in its shaft bearing. In practice, it is difficult to determine the prohibited zone by actual performance testing or operating records. In actual operation, the best economy is achieved by avoiding operation in these areas [5]. Hence, the feasible operation zone of unit i can be given as follows:
|
|
(11) |
where ![]() and
and ![]() are the lower
and upper bound of the kth prohibited zone
of generator i
are the lower
and upper bound of the kth prohibited zone
of generator i
Overview of Differential Evolution Algorithm
The differential Evolution algorithm (DE) is a population based algorithm like genetic algorithm using the similar operators; crossover, mutation and selection. The main difference in constructing better solutions is that genetic algorithms rely on crossover while DE relies on mutation operators. This main operation is based on the differences of randomly sampled pairs of solutions in the population.
The algorithm uses mutation operation as a search mechanism and selection operation to direct the search toward the prospective regions in the search space. The DE algorithm also uses a non-uniform crossover that can take child vector parameters from one parent more often than it does from other. By using the components of the existing population members to construct trial vectors, the recombination (crossover) operator efficiently shuffles information about successful combinations, enabling the search for a better solution space.
DE Optimization Procedure
An optimization task consisting of D parameters can be presented by a D-dimensional vector. In DE, a population of NP solution vectors is randomly created at the start. This population is successfully improved over G generations by applying mutation, crossover and selection operators, to reach an optimal solution [3, 4]. The main steps of the DE algorithm are given bellow [6]:
Initialization
Evaluation
Repeat
Mutation
Crossover
Evaluation
Selection
Until (Termination criteria are met)
Mutation
The mutation operator creates mutant vectors by perturbing a randomly selected vector xa with the difference of two other randomly selected vectors xb and xc,
|
|
(12) |
where xa, xb and xc are randomly chosen vectors among the NP population, and a ≠ b ≠ c. xa, xb and xc are selected anew for each parent vector. The scaling constant F is an algorithm control parameter used to adjust the perturbation size in the mutation operator and improve algorithm convergence.
Crossover
The crossover operation generates trial vectors xi by mixing the parameters of the mutant vectors xi with the target vectors xi according to a selected probability distribution,
|
|
(13) |
where i=1,
, NP and j=1,
, D; q is a randomly chosen
index ![]() {1,
,Np} that guarantees that the trial vector gets at
least one parameter from the mutant vector; ρj is a uniformly distributed random
number within [0 , 1] generated anew for each value of j. The crossover
constant CR is an algorithm parameter that controls the diversity of
the population and aids the algorithm to escape from local minima. xj,i(G)
and xj,i(G) are
the jth parameter of the ith target vector, mutant vector, and trial
vector at generation G, respectively.
{1,
,Np} that guarantees that the trial vector gets at
least one parameter from the mutant vector; ρj is a uniformly distributed random
number within [0 , 1] generated anew for each value of j. The crossover
constant CR is an algorithm parameter that controls the diversity of
the population and aids the algorithm to escape from local minima. xj,i(G)
and xj,i(G) are
the jth parameter of the ith target vector, mutant vector, and trial
vector at generation G, respectively.
Selection
The selection operator forms the population by choosing between the trial vectors and their predecessors (target vectors) those individuals that present a better fitness or are more optimal according to (10).
|
|
(14) |
This optimization process is repeated for several generations, allowing individuals to improve their fitness as they explore the solution space in search of optimal values.
DE has three essential control parameters: the scaling factor (F), the crossover constant (CR) and the population size (NP). The scaling factor is a value in the range [0, 2] that controls the amount of perturbation in the mutation process. The crossover constant is a value in the range [0, 1] that controls the diversity of the population. The population size determines the number of individuals in the population and provides the algorithm enough diversity to search the solution space.
Control Parameter Selection
Proper selection of control parameters is very important for algorithm success and performance. The optimal control parameters are problem specific. Therefore, the set of control parameters that best fit each problem have to be chosen carefully. The most common method used to select control parameters is parameter tuning. Parameter tuning adjusts the control parameters through testing until the best settings are determined. Typically, the following ranges are good initial estimates [7]: F = [0.5, 0.6], CR = [0.75, 0.90], and NP = [3*D, 8*D].
Constraint Handling
Since most evolutionary algorithms such as differential evolution were originally conceived to solve unconstrained problems, various constraint-handling techniques have been developed. One possible strategy is to generate and keep control variables in the feasible region as follows [7]:
|
|
(15) |
where xj,imin and xj,imax are the lower and upper bounds of the jth decision parameter, respectively.
In the fitness evaluation, penalty functions can be used whenever there are violations to some equality and/or inequality constraints [8]. Basically, the objective function is substituted by a fitness function FT that penalizes the fitness whenever the solution contains parameters that violate the problem constraints. The extended objective function (fitness function) can be defined as:
|
|
(16) |
where K is the penalty factor of the equality constraint
Adaptive Differential Evolution Algorithm
As presented above, In DE, the fitness of an offspring is one-to-one competed with that of the corresponding parent. This one-to-one competition makes convergence speed of DE faster than other evolutionary algorithms. Nevertheless, this faster convergence property yields in a higher probability of searching toward a local optimum or getting premature convergence [9, 10].
The original DE uses a fixed positive values for the scaling factor F and the crossover constant CR. This has an effect of restricting the exploration of the solution space, leading to a premature convergence. Thus, the optimal selection of these control parameters is very important in the success of the algorithm, as different parameter settings may lead to different results.
In this study, a new strategy in the selection of the parameter settings of DE algorithm is proposed. The basic idea is the development of an adaptive differential evolution algorithm, where the parameter of mutation and crossover is evolved rather than being fixed throughout the optimization process. The adaptation strategy is carried out by integrating the scaling factor F and crossover constant CR in the population. This strategy explores effectively the solution space, maintains the exploratory feature and at the same time expedites the convergence.
Simulation Results
To illustrate the performance of the proposed adaptive differential evolution (ADE) approach, experiments are performed on the 6-unit power system, which considers the prohibited operating zones, ramp rate limits, and transmission network losses. This system contains six thermal units, 26 buses, and 46 transmission lines [11]. The required power demand to be met by all the six generating units is 1263 MW. Input data are shown in Table 1 and the loss coefficients with the 100-Mva base capacity are given bellow [11].
Simulations were carried out using MATLAB computational environment, on an Intel Core2 Duo 2.10 GHz Laptop computer with 3 GB RAM under Windows 7.
Table 1. Data of the 6-unit system
|
Unit |
(MW) |
(MW) |
ci ($) |
bi ($/MWh) |
ai ($/MW2h) |
(MW) |
URi (MW/h) |
DRi (MW/h) |
Prohibited zones (MW) |
|
1 |
100 |
500 |
240 |
7.0 |
0.0070 |
440 |
80 |
120 |
[210240] [350380] |
|
2 |
50 |
200 |
200 |
10.0 |
0.0095 |
170 |
50 |
90 |
[90110] [140160] |
|
3 |
80 |
300 |
220 |
8.5 |
0.0090 |
200 |
65 |
100 |
[150170] [210240] |
|
4 |
50 |
150 |
200 |
11.0 |
0.0090 |
150 |
50 |
90 |
[8090] [110120] |
|
5 |
50 |
200 |
220 |
10.5 |
0.0080 |
190 |
50 |
90 |
[90 110] [140150] |
|
6 |
50 |
120 |
190 |
12.0 |
0.0075 |
110 |
50 |
90 |
[7585] [100105] |
|
|
(17) |
|
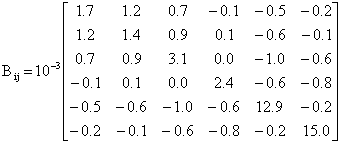
Bi0 = 10-3[-0.3908 -0.1297 0.7047 0.0591 0.2161 -0.6635] |
(18) |
|
B00 = 0.0056 |
(19) |
In order to demonstrate the efficiency and robustness of the proposed algorithm, 100 independent runs were performed using the control parameter settings listed in Table 2.
The average cost found by ADE was 15449.34 $/h with a minimum cost of 15448.82 $/h, and a maximum cost of 15462.89 $/h (0.09% difference). The average execution time of the ADE for this test system is 1.01 s, which is very acceptable computation time for ELD solution. Also, it is important to point out that for all the trial runs, the convergence was reached without any violation of the generator constraints.
Table 3 presents a summary of the optimization results for the solution with minimum cost, which converged after 360 generations and 1.11 s. It is clear that the best solution obtained by ADE satisfies the system constraints such as the ramp rate limits and prohibited operating zones. The convergence of ADE for the trial run that produced the minimum cost solution is shown in Fig. 1.
Table 2. Control parameter settings of ADE algorithm
|
Parameter |
Setting |
|
Population size (Np) |
30 |
|
Maximum number of generations (Gmax) |
500 |
|
Scaling factor range F |
[0.5 1.0] |
|
Probability of crossover range (CR) |
[0.5 1.0] |
|
Penalty factor (K) |
6Χ105 |
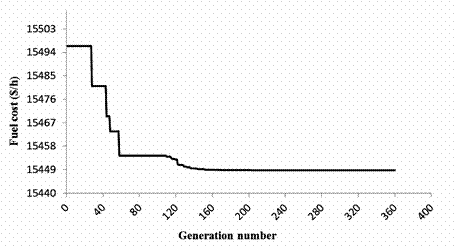
Figure 1. Convergence of the best solution found with ADE
The best economic dispatch solution of the proposed approach were compared in Table 3 to those reported using particle swarm optimization (PSO) [11], genetic algorithm (GA) [11], adaptive particle swarm optimization (APSO) [12], binary successive approximation based evolutionary search (BSA-EV) [13], distributed sobol PSO with tabu search algorithm (DSPSO-TSA) [14] and differential evolution (DE) [15].
From Table 3, it is obvious that ADE is superior to the original differential algorithm (DE) with regard to the solution quality. It can be seen also that the results given by ADE are better than those reported in the literature, except for the solutions of APSO, BSA-EV and DSPSO-TSA reported in Panigrahi [12], Dhillon [13] and Khamsawang [15], respectively, which are less expensive. However, it is important to note that in the cases of the APSO, BSA-EV and DSPSO-TSA methods, the power balance constraint (6) is not satisfied. Indeed, by using the loss formula (7), the actual transmission losses obtained from the depicted generation schedules of APSO, BSA-EV and DSPSO-TSA, are: 12.862 MW, 12.981 MW and 13.148 MW, respectively. The errors in the power balance constraint of these three last methods are provided in Table 4, which shows that the error of ADE is tolerable (0.08 MW) and is the lowest compared with those of APSO, BSA-EV and DSPSO-TSA. As a conclusion, we can say that the proposed ADE approach has the ability to find the best accurate economic dispatch solutions compared to those obtained with recent heuristic approaches.
Table 3. Comparison of the best solution obtained by ADE
|
Power output (MW) |
PSO [11] |
GA [11] |
APSO [12] |
BSA-EV [13] |
DSPSO-TSA [14] |
DE [15] |
Proposed ADE |
|
P1 |
447.497 |
474.807 |
446.669 |
456.680 |
439.293 |
447.744 |
447.486 |
|
P2 |
173.322 |
178.636 |
173.156 |
170.676 |
187.788 |
173.407 |
173.307 |
|
P3 |
263.474 |
262.209 |
262.826 |
265.000 |
261.026 |
263.411 |
263.450 |
|
P4 |
139.059 |
134.283 |
143.469 |
136.540 |
129.497 |
139.076 |
139.056 |
|
P5 |
165.476 |
151.904 |
163.914 |
161.852 |
171.710 |
165.364 |
165.455 |
|
P6 |
87.128 |
74.181 |
85.344 |
84.728 |
86.165 |
86.944 |
87.123 |
|
Total power (MW) |
1276.010 |
1276.030 |
1275.376 |
1275.477 |
1275.514 |
1275.947 |
1275.877 |
|
Loss (MW) |
12.958 |
13.022 |
12.422 a(12.862) |
12.477 a(12.981) |
13.042 a(13.148) |
12.957 |
12.957 |
|
Total cost ($/h) |
15450.00 |
15459.00 |
15444.00 |
15444.01 |
15441.57 b(15444.61) |
15449.77 |
15448.82 |
|
a Represents the actual transmission loss as per given generation schedule. b Denotes the exact fuel cost obtained from the above schedule. |
|||||||
Table 4. Errors engendered by APSO, BSA-EV, DSPSO-TSA and ADE methods
|
|
APSO [12] |
BSA-EV [13] |
DSPSO-TSA [15] |
ADE |
|
Error in MW |
0.49 |
0.50 |
0.63 |
0.08 |
Table 5 presents the minimum, average and maximum costs of 100 trials for ADE, which are compared with other heuristic techniques available in the literature. From this Table, we can see that ADE gives the best average cost with reference to the satisfaction of the energy balance constraint. It is noted that the execution times of the DEPSO are not compared with that of the other techniques, since the solution times of each method are measured on a different hardware.
The statistical results of 100 runs by ADE with 100 different initial trial solutions are depicted in Fig. 2. This figure shows that 91% of the solutions are within 0.005% of the minimum cost (15448.82 $/h), indicating a good convergence characteristic. It can be concluded that ADE algorithm is robust and effective in solving the ELD problem considering practical generator operation constraints, such us prohibited operating zones and ramp rate limits.
Table 5. Comparison of simulation results
|
Method |
Minimum cost ($/h) |
Average cost ($/h) |
Maximum cost ($/h) |
|
PSO [11] |
15450.00 |
15454.00 |
15492.00 |
|
GA [11] |
15459.00 |
15469.00 |
15524.00 |
|
APSO [12] |
15443.58 |
15449.99 |
NA |
|
BSA-EV [13] |
15444.01 |
NA |
NA |
|
DSPSO-TSA [14] |
15441.57 *(15444.61) |
15443.84 |
15446.22 |
|
DE [15] |
15449.77 |
15449.78 |
15449.87 |
|
Proposed ADE |
15448.82 |
15449.34 |
15462.89 |
|
Note: NA, Not available. * Denotes the exact fuel cost obtained from the best schedule reported in [14]. |
|||
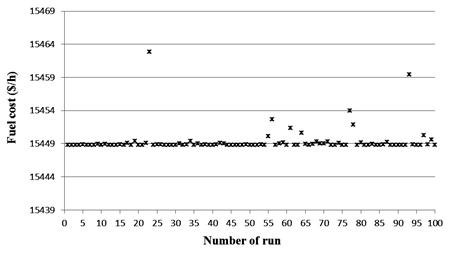
Figure 2. Distribution of fuel cost achieved by ADE
Conclusion
In this study, an efficient approach based on the adaptive differential evolution (ADE) algorithm was developed and successfully applied to solve the economic load dispatch problem with taking into account nonlinear generator features such as ramp rate limits and prohibited operating zones. A dynamic mutation and crossover parameters are suggested in order to improve the global and local search abilities of the proposed ADE.
The feasibility of the proposed ADE was demonstrated on the 6-unit benchmark test system. Simulation results have demonstrated that the proposed improvement was a powerful strategy to prevent premature convergence to local minima, providing high quality solutions. Also, ADE algorithm has shown superior features such as accurate solution, stable convergence characteristic, and good computation efficiency, compared to other heuristics reported in the literature recently.
References
1. Wong K.P., Yuryevich J., Optimal power flow method using evolutionary programming, Springer-Verlag Berlin, 1999, p. 405-412.
2. Price K., Differential Evolution: a fast and simple numerical optimizer, Biennial Conference of the North American Fuzzy Information Processing Society NAFIPS, 19-22 June 1996, p. 524-527.
3. Storn R., On the usage of differential evolution for function optimization, Biennial Conference of the North American Fuzzy Information Processing Society NAFIPS, 19-22 June 1996, p. 519-523.
4. Storn R., Price K., Differential Evolution a simple and efficient adaptive scheme for global optimization over continuous spaces, Journal of Global Optimization, 1997, 11, p. 341-359.
5. Lee F.N., Breipohl A.M., Reserve constrained economic dispatch with prohibited operating zones, IEEE Transactions on Power Systems, 1993, 8, p. 246254.
6. Sayah S., Zehar K., Using evolutionary computation to solve the economic load dispatch problem, Leonardo Journal of Sciences, 2008, 12, p. 67-78.
7. Pιrez-Guerrero R.E., Cedeρo-Maldonado J. R., Differential evolution based economic environmental power dispatch, in Proceedings of the 37th Annual North American Power Symposium, 23-25 October 2005, p. 191-197.
8. Chong E.K.P., An introduction to optimization, John Wiley & Sons, Inc., New York, 2001.
9. Sayah S., Zehar K., Modified differential evolution algorithm for optimal power flow with non-smooth cost functions, Int. J. Energy Conversion and Management, 2008, 49, p. 3036-3042.
10. He D., Wang F., Mao Z., A hybrid genetic algorithm approach based on differential evolution for economic dispatch with valve-point effect, Int. J. Electrical Power and Energy Systems, 2008, 30, p. 31-38.
11. Gaing Z-L, Particle swarm optimization to solving the economic dispatch considering generator constraints, IEEE Transactions on Power Systems, 2003, 18, p. 11871195.
12. Panigrahi B.K., Pandi V.R., Das S., Adaptive particle swarm optimization approach for static and dynamic economic load dispatch. Int. J. Energy Conversion and Management, 2008, 49, p. 1407-1415.
13. Dhillon J.S., Dhillon J.S., Kothari D.P., Economic-emission load dispatch using binary successive approximation-based evolutionary search, IET Gener. Transm. Distrib., 2009, 3, p. 1-16.
14. Khamsawang S., Jiriwibhakorn S., DSPSOTSA for economic dispatch problem with nonsmooth and noncontinuous cost functions, Int. J. Energy Conversion and Management, 2010, 51, p. 365-375.
15. Noman N, Iba H., Differential evolution for economic load dispatch problems, Electric Power Systems Research, 2008, 78, p.1322-1331.
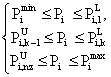 , k = 1,
,
, k = 1,
, 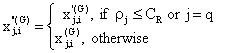
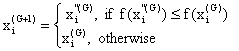
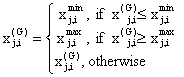
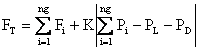 ,
,