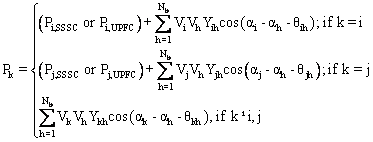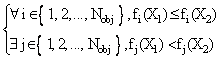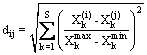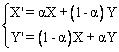Application of Multi-Objective Evolutionary Algorithm for Optimal Reactive Power Dispatch with Flexible AC Transmission System Devices
Ismail MAROUANI*, Tawfik GUESMI, Hsan HADJ ABDALLAH, and Abdarrazak OUALI
*
E-mail*: ismail.marouani@isetks.rnu.tn
Abstract
Because their capability to change
the network parameters with a rapid response and enhanced flexibility, flexible
AC transmission system (
Keywords
Multi-objective
optimization; Evolutionary algorithms; Power flow; SSSC;
Introduction
The ORPD problem is considered as a MOP. It consists to improve the voltage profile and minimize the real power loss in transmission lines under several equality and inequality constraints. Such as, load flow equations and security limits. To maintain the load buses voltage within their permissible limits many technical methods are proposed [1, 2], such as, reallocating reactive power generation in the system adjusting transformer taps, generator voltage and switchable reactive power sources. To minimize system losses, a redistribution of reactive power in the network can be used [3].
Because the recent progress of power electronics, FACTS devices have taken more attention in transmission power systems. They have the capability to change the network parameters with a rapid response and enhanced flexibility, such as, improving voltage profile and minimizing system losses.
Some types of those devices, are,
static synchronous series compensator (SSSC), static synchronous compensator
(STATCOM) and unified power flow controller (
SSSC is considered as a controllable
voltage source inverter that is connected in series with transmission line.
This injected voltage is almost in quadrature with the line current.
Consequently, it provides a variable reactance in series with the transmission
line, which, can be inductive or capacitive. This reactance controls the power
flow in the line where it is introduced. The STATCOM is a shunt connected FACTS
devices. It consists of a voltage source converter linked to the system via a
shunt transformer. Its principal function is to ameliorate the voltage profile
at the point of connection. To exploit the benefits of those two devices, the
Therefore, in first step, the objective of the present paper is to develop a power flow model for power system with FACTS devices. The modified Newton-Raphson power flow algorithm was used [4]. Then, a new ORPD problem is formulated. The solutions of this problem are the FACTS parameters and location.
In a MOP, there isn’t one solution that is best with respect to all objectives. Generally, the aim is to determine the trade-off surface, which is a set of non-dominated solution points, known as Pareto optimal solutions. Every individual of this set is an acceptable solution.
In the literature, several methods are used to solve the ORPD. In [2], a nonlinear programming technique was used. Gradient-based optimization algorithms consist to linearize the objective functions and the system constraints around an operating point was presented in [3]. Those traditional techniques consume an important computing time and they are iterative methods. Also, they can converge to a local optimum.
Recently, genetic algorithms (GA) are very much used to solve MOP. Many researchers have transformed the MOP to a single objective problem using appropriate weights. Then, GA was been applied [5]. Unfortunately, the obtained solution depends on the weight vector used in the process. Also, this method requires a number of runs equal to the size of the desired Pareto optimal solutions.
MOEAs are used to eliminate most
difficulties of these methods. MOEAs are no iterative and they give the Pareto
optimal solutions in one run. Thus, in this article a no conventional technique
based on MOEA is employed. It is based on non-dominated Sorting Genetic
Algorithm II (N
Static models of two FACTS devices
consisting of
Material and Method
Modelling of Power Systems with Multiple FACTS
As indicated previously, SSSC and
SSSC Mathematical Modelling
Figure 1 show's the circuit model of
an SSSC connected at position d between two buses n and m.
So, another two buses i and j are added to the total number of
buses of the system (where d is the portion of the impedance of line n-m, ![]() ).
).
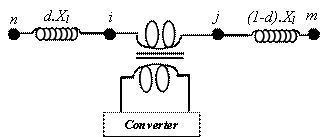
Figure 1. SSSC location between buses n and m
In its equivalent circuit shown in Figure 2, the SSSC is represented by a voltage source Vse in series with the transformer impedance Xs [6, 7]. In practice, Vse can be regulated to control the power flow of line m-n and the voltage at buses i and j.

Figure 2. Voltage-source model of SSSC
This last model can be developed by replacing voltage source Vse by a current source Ise parallel with the transmission line as shown in Figure 3.

Figure 3. Replacement of series voltage source by a current source
|
Ise = -jbseVse |
(1) |
|
Vse=rViejγ |
(2) |
r and γ are respectively the p.u. magnitude and phase angle of series voltage source.
0 ≤ r ≤ rmax and 0 ≤ γ ≤ 2π
The power injection model of the SSSC can be seen as two dependent power injections at auxiliary buses i and j as shown in Figure 4 [8].

Figure 4. SSSC mathematical model
The apparent power supplied by the model is calculated as:
|
Si = Vi(-Ise)* |
(3) |
|
Sj = Vj(Ise)* |
(4) |
Then, active and reactive power supplied by the SSSC can be deduced from
Equations (5) to (8).
|
Pi,SSSC = -rbseVi2sin(γ) |
(5) |
|
Qi,SSSC = -rbseVi2cos(γ) |
(6) |
|
Pi,SSSC = rbseViVjsin(αi-αj+γ) |
(7) |
|
Qi,SSSC = rbseViVjcos(αi-αj+γ) |
(8) |
An
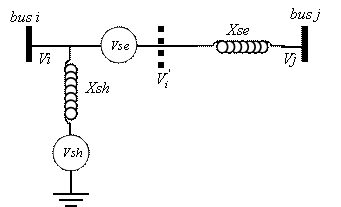
Figure 5. Two voltage-source model of
Vse is defined as in equation (2).
The voltage source Vse in the last model can be replaced by a current source Ise parallel with the transmission line as shown in Figure 3.
The shunt branch in
If the total losses of the two
converters are estimated to be about 2% of Pseries, then, the provided
power by shunt branch Pshunt will be expressed by [4]:
|
Pshunt = -1,02Pserie |
(9) |
The function of the reactive power
delivered or absorbed by the shunt branch is to maintain the level of tension
to bus i within acceptable limits. Finally,
The elements of equivalent
power injection in Figure 6 are:
|
Pi,ufc = 0,02rbseVi2sinγ-1,02rbseViVjsin(αi-αj+γ) |
(10) |
|
Pj,upfc = rbseViVjsin(αi-αj+γ) |
(11) |
|
Qi,upfc = -rbseViVjcos(γ) |
(12) |
|
Qj,upfc = rbseViVjcos(αi-αj+γ) |
(13) |

Figure 6.
Problem Formulation
The ORPD problem is to optimise the steady performance of a power system in terms of one or more objective functions while satisfying several equality and inequality constraints.
In this section, we suppose that the extremities FACTS devices are referred by bus i and j.
Objective Functions
In this paper two objective functions are used.
i. Real power loss
This objective consists to minimise
the real power loss PL in
transmission lines that can be expressed as [1, 11]:
|
|
(14) |
|
|
(15) |
where:
Nb : number of buses;
Vk<αk and Vh<ah : respectively voltages at bus k and h;
Ykh and qkh: respectively modulus and argument of the kh-th element of the nodal admittance matrix Y.
ii. Voltage deviation
This objective is to minimize the
deviation in voltage magnitude at load buses that can be expressed as:
|
|
(16) |
where:
NL: number of load buses;
![]() : prespecified
reference value of the voltage magnitude at the i-th load bus.
: prespecified
reference value of the voltage magnitude at the i-th load bus.
![]() is
usually set to be 1.0 p.u.
is
usually set to be 1.0 p.u.
Problem Constraints
The problem constraints are divided to equality and inequality constraints.
i. Equality constraints
These constraints represent typical
load flow equations as follows:
|
|
(17) |
|
|
(18) |
where:
PGi and QGi: generator real and reactive power at i-th bus, respectively;
PDi and QGi: load real and reactive power at i-th bus, respectively;
Gij and Bij: transfer conductance and susceptance between buses i and j, respectively.
ii. Inequality constraints
These constraints can be summarized by:
(a) Security constraints
These include the constraints of
voltage at the i-th load buses VLi as follows:
|
|
(19) |
(b) Parameters FACTS constraints
|
rmin ≤ r ≤ rmax |
(20) |
|
γmin ≤ γ ≤ γmax |
(21) |
|
dmin ≤ d ≤ dmax |
(22) |
We should note that the vector of decision variables is U = [r,g,d].
Multi-Objective Optimization
In a MOP, there may not exist one solution that is best with respect to all objectives. Usually, the aim is to determine the trade-off surface, which is a set of nondominated solution points, known as Pareto optimal solutions. Every individual in this set is an acceptable solution.
For any two X1 and X2,
we can have one of two possibilities: one dominates the other or none dominates
the other. In a minimization problem, we say that the solution X1
dominates X2, if the following two conditions are satisfied [12]:
|
|
(23) |
where:
Nobj : Number of objective functions;
fi : i-th objective function.
The goal of a multi-objective optimization algorithm is not only to guide the search towards the Pareto optimal front, but, also to maintain population diversity in the set of the nondominated solutions.
In the rest of this section, we will present the elitist MOEA NSGAII. So, we must be start with a presentation of the NSGA approach.
NSGA Approach
The basic idea behind NSGA is the
ranking process executed before the selection operation. The ranking procedure
consists to find the nondominated solutions in the current population P.
These solutions represent the first front F1. Afterwards, this first
front is eliminated from the population and the rest is processed in the same
way to identify nondominated solutions for the second front F2. This
process continues until the population is properly ranked. So, can write [13]:
|
|
(24) |
where, r is the number of fronts.
The same fitness value fk
is assigned to all of individuals of the same front Fk. This fitness
value decreases while passing from the front Fk to the Fk+1.
To maintain diversity in the population, a sharing method is used. Let consider
dij the variable distance (Euclidean norm) between two solutions ![]() and
and ![]() .
.
|
|
(25) |
where S is the number of variables
in the MOP. The parameters ![]() and
and
![]() respectively
are the upper and lower bounds of variable Xk.
respectively
are the upper and lower bounds of variable Xk.
|
|
(26) |
The sharing procedure is as follows:
Step 1: Fix the niche radius sshare and a small positive number e.
Step 2: Initiate fmin = Npop+e and the counter of front j =1.
Step 3: From the r nondominated
fronts Fj which constitute P.
|
|
(27) |
Step 4: For each individual
![]() :
:
· associate the dummy fitness fj(q) = fmin - ε;
· calculate the niche count ncq as given in [13];
·
calculate the shared fitness ![]()
![]() .
.
Step 5: ![]() and j = j + 1.
and j = j + 1.
Step 6: If j ≤ r, then, return to step 4. Else, the process is finished.
The MOEAs using nondominated sorting and sharing have been criticized mainly for their O(MN3) computational complexity (M is the number of objectives and N is the population size). Also, these algorithms are not elitist approaches and they need to specify the sharing parameter. To avoid these difficulties, we present in the following an elitist MOEA which is called Nondominated Sorting Genetic Algorithm II (NSGAII).
NSGAII Approach
In this approach, the sharing function approach is replaced with a crowded comparison.
Initially, an offspring population Qt
is created from the parent population Pt at the tth
generation. After, a combined population Rt is formed [13].
![]()
Rt is sorted into
different no domination levels Fj as shown in the NSGA approach. So,
we can write:
![]() , where, r is number fronts.
, where, r is number fronts.
Finally, one iteration of the NSGAII procedure is as follows:
Step 1: Create the offspring population Qt from the current population Pt.
Step 2: Combine the two populations Qt and Pt to form Rt.
Step 3: Find the all nondominated fronts Fi and Rt.
Step 4: Initiate the new population Pt+1 = f and the counter of front for inclusion i = 1.
Step 5: While |Pt+1| + |Fi|
≤ Npop, do:
![]()
![]()
Step 6: Sort the last front Fi using the crowding distance in descending order and choose the first (Npop - |Pt+1|) elements of Fi.
Step 7: Use selection, crossover and mutation operators to create the new offspring population Qt+1 of size Nobj.
To estimate the density
of solution surrounding a particular solution ![]() in a nondominated set F,
we calculate the crowding distance as follows:
in a nondominated set F,
we calculate the crowding distance as follows:
Step 1: Let’s suppose q = |F|. For
each solution ![]() in F,
set di = 0.
in F,
set di = 0.
Initiate m = 1.
Step 2: Sort F in the descending order according to the objective function of rank m.
Let’s consider ![]() the vector of indices,
i.e. Iim is the index of the solution
the vector of indices,
i.e. Iim is the index of the solution ![]() in the sorted list according
to the objective function of rank m.
in the sorted list according
to the objective function of rank m.
Step 3: For each solution ![]() which verifies 2 ≤
Iim ≤ (q-1), update the value of di as
follows:
which verifies 2 ≤
Iim ≤ (q-1), update the value of di as
follows:
|
|
(28) |
Then, the boundary solutions in the sorted list (solutions with smallest and largest function) are assigned an infinite distance value, i.e. if, Iim = 1 or Imi = q, di = ∞.
Step 4: If m = M, the procedure is finished. Else, m = (m+1), and return to step 2.
Implementation of the NSGAII
The proposed NSGAII has been
implemented using real-coded genetic algorithm (RCGA) [14]. So, a chromosome X
corresponding to a decision variable is represented as a string of real values
xi, i.e. X=x1x2…xlchrom. lchrom is
the chromosome size and xi is a real number within its lower limit ai
and upper limit bi. i.e. ![]() . Thus, for two
individuals having as chromosomes respectively X and Y and after generating a
random number
. Thus, for two
individuals having as chromosomes respectively X and Y and after generating a
random number![]() , the
crossover operator can provide two chromosomes X’ and Y’ with a probability Pc
as follows [13]:
, the
crossover operator can provide two chromosomes X’ and Y’ with a probability Pc
as follows [13]:
|
|
(29) |
In this study, the non-uniform
mutation operator has been employed. So, at the tth generation, a
parameter xi of the chromosome X will be transformed to other
parameter ![]() with a
probability Pm as follows:
with a
probability Pm as follows:
|
|
(30) |
|
|
(31) |
Where t is a random binary number, r is a random
number ![]() and gmax
is the maximum number of generations. b is a positive constant chosen arbitrarily.
and gmax
is the maximum number of generations. b is a positive constant chosen arbitrarily.
Results and Discussion
The proposed procedure for solving dispatch VAR including FACTS devices is tested on the 6-bus system [16]. The one-line diagram of this system is shown in Figure 7. The system consists of three generators at buses 4, 5 and 6. Bus 6 is considered at the slack bus. Buses 1, 2 and 3 are the load buses.
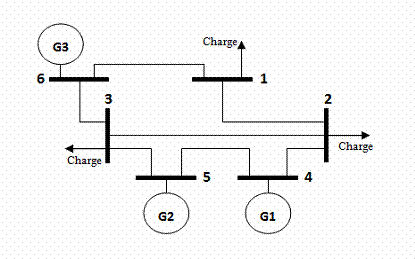
Figure 7. Test system
Presentation of the Test System
The characteristics of lines and buses are marked in the Tables 1 and 2 respectively. These values are given in p.u. considering a base power of 100 MVA for the overall system and base voltages of 100 KV. The lower voltage magnitude limits at all buses are 0.9 p.u and the upper limits are 1.1 p.u. Three cases of power analysis are considered. Case 1 assumes the study without any compensation. Case 2 assumes an SSSC between two load buses. In case 3, an UPFC is assumed too between two load buses.
Table 1. Data lines
|
Line |
Impedance |
||
|
Bus i |
Bus j |
R |
X |
|
1 |
2 |
0.02 |
0.4 |
|
1 |
6 |
0.01 |
0.15 |
|
2 |
3 |
0.05 |
0.5 |
|
2 |
4 |
0.015 |
0.5 |
|
3 |
5 |
0.05 |
0.5 |
|
3 |
6 |
0.05 |
0.5 |
|
4 |
5 |
0.08 |
0.8 |
Table 2. Data buses
|
Bus |
V |
PG |
QG |
PD |
QD |
|
1 |
- |
0 |
0 |
0.840 |
0.500 |
|
2 |
- |
0 |
0 |
0.400 |
0.400 |
|
3 |
- |
0 |
0 |
0.96 |
0.300 |
|
4 |
1.025 |
0.200 |
- |
0.100 |
0.100 |
|
5 |
1.084 |
0.100 |
- |
0.100 |
0.100 |
|
6 |
1.000 |
- |
- |
0.100 |
0.100 |
Figure 8 shows the convergence characteristics of the load flow program after 6 iterations with a tolerance of 10-5.
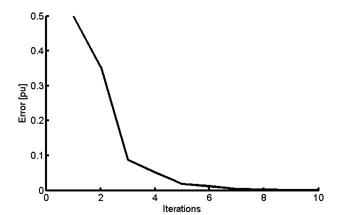
Figure 8. Convergence of the load flow
For the system without FACTS controllers, the voltage magnitude of load buses given by the load flow program, are not maintained within their permissible limits (Table 3).
Table 3. Voltage magnitudes and phase angles for the system without FACTS controllers
|
Bus |
1 |
2 |
3 |
4 |
5 |
6 |
|
V |
0.828 |
0.868 |
0.947 |
1.025 |
1.084 |
1.00 |
|
α [rad] |
-0.299 |
-0.367 |
-0.195 |
-0.268 |
-0.141 |
0 |
The corresponding values of voltage deviation and real power loss are respectively:
VD = 0.441 pu and PL = 0.133 pu.
Resolution of the ORPD
After execution of the optimization program, the values of the voltage deviation and the real power losses for the various positions of elements FACTS, are given in Figure 9.
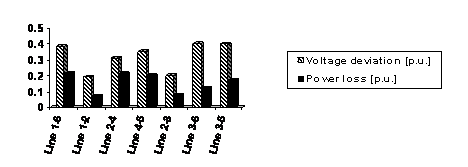
(a)
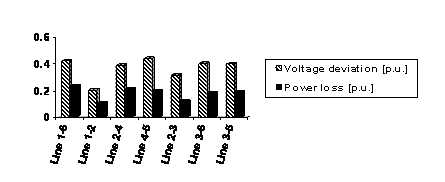
(b) SSSC
Figure 9. The best position for system FACTS
Figure 9 shows that the best
position of
Therefore, we will give only the results corresponding to this optimal position.
Optimisation Mono Objective
To get convergence of power loss and voltage deviation functions which are shown in Figures 10 and 11, these two objective functions are optimized individually.
Figure 10 shows the convergence of power losses function versus number of generations.
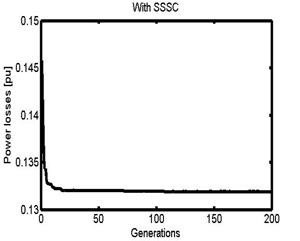
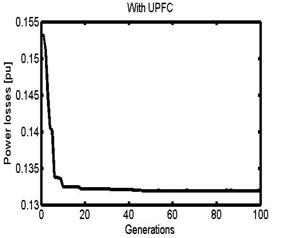
Figure 10. Convergence of power losses with generations
From Figure 11, we can see that
voltage deviation corresponding to the two cases converges to 0.418 pu and
0.375 pu, respectively, for the system with SSSC and with
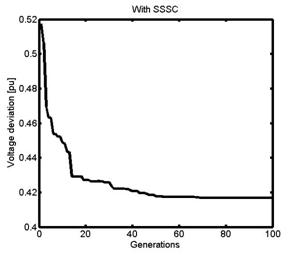
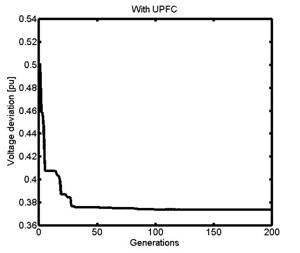
Figure 11. Convergence of voltage deviation with generations
Optimization Bi-Objective
In this section, the two objective functions are optimized simultaneously.
Figure 12 gives the Pareto-optimal
front corresponding to the two cases. And it shows that the
After optimization by the NSGAII approach, we have obtained the Tables 4 and 5 giving the best solutions for minimum voltage deviation and minimum real power loss respectively.
The values of r, d, VD and PL are given in p.u. g is in radian.
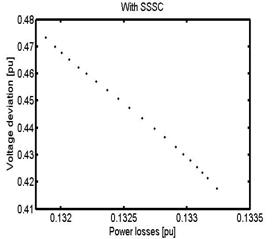
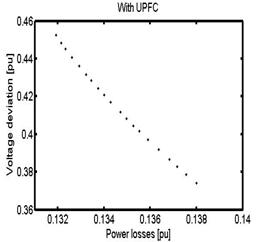
Figure 12. Pareto-optimal front of the proposed approach
Table 4. The best solution for voltage deviation
|
|
R |
g |
d |
VD |
Corresp. PL |
|
SSSC |
0.1525 |
1.253 |
0.442 |
0.418 |
0.133 |
|
|
0.1931 |
1.481 |
0.485 |
0.375 |
0.138 |
Table 5. The best solution for real power loss
|
|
R |
g |
d |
PL |
Corresp. VD |
|
SSSC |
0.1537 |
1.128 |
0.461 |
0.132 |
0.46 |
|
|
0.1952 |
1.369 |
0.527 |
0.132 |
0.45 |
Table 6. For minimum voltage deviation
|
|
V1 [pu] |
V2 [pu] |
V3 [pu] |
|
SSSC |
0.9821 |
0.9274 |
0.9365 |
|
|
0.9915 |
0.9691 |
0.9467 |
Table 7. For minimum real power loss
|
|
V1 [pu] |
V1 [pu] |
V1 [pu] |
|
SSSC |
0.9778 |
0.9146 |
0.9217 |
|
|
0.9870 |
0.9541 |
0.9406 |
The profile voltage in load buses corresponding to the best solutions given in Tables 4 and 5 are shown respectively in Tables 6 and 7. Vi is in pu.
Conclusion
In this paper, a procedure based on
MOEA to solve ORPD problem with FACTS was presented. This problem consists to
minimize simultaneously real power loss in transmission lines and voltage deviation
at load buses by using FACTS devices. The decision variables are parameters and
location of FACTS devices. The NSGAII approach is opted to solve this nonlinear
MOP.
Acknowledgments
This paper extends and completes a previous communicated research [Marouani I. Guesmi T.; Abdallah H. H.; Ouali, A. Application of a multiobjective evolutionary algorithm for optimal location and parameters of FACTS devices considering the real power loss in transmission lines and voltage deviation buses. 6th International Multi-Conference on Systems, Signals and Devices, 2009. SSD '09. DOI: 10.1109/SSD.2009.4956757 (6pages)].
References
1. Abido M.A., Bakhashwain J.M., Optimal VAR dispatching using a multiobjective evolutionary algorithm, Electrical Power and Energy System, 2005, 27(1), p. 13-20.
2. Ben Aribia H., Hadj Abdallah H., Multi Objectives Reactive Dispatch Optimisation, Leonardo Journal of Sciences (LJS), 2007, 6(10), p. 101-114.
3. Mamandur K.R.C., Chnoweth R.D., Optimal control of reactive power flow for improvement in voltage profiles and for real power loss minimization, IEEE Trans Power Apparat Syst. 1981; PAS-100(7), p. 3185-3194.
4. Mete Vural A., Tumay Mehmet, Mathematical modelling and analysis of unfied power flow controller: A comparison of two approaches in power flow studies and effects of UPFC location, Electrical Power and Energy Systems, 2007, 29(8), p. 617-629.
5.
Mishra S., Dash P.K., Hota
P.K., Tripathy M., Genetically optimized neuro-fuzzy PFC for damping modal
oscillations of power system,
6. Ghadir Radman, Reshma S. Raje, Power flow model/calculation for power systems with multiple FACTS controllers, Electric Power Systems Research, 2007, 77(12), p. 1521-1531.
7. Sen K.K., SSSC-static synchronous series compensator: Theory, modelling, and application, IEEE Trans. Power Delievery, 1998, 13(1), p. 241-246.
8. Zhang X.P., Advanced modelling of multicontrol functional static synchronous series compensator (SSSC) in Newton-Raphson power flow, IEEE Trans.Power Syst., 2003, 18(4), p. 1410-1416.
9. Fuerte-Esquivel C.R., Acha E., Unified power flow controller: a critical comparaison of Newton-Raphson UPFC algorithms in power flow studies, IEE Proc. Generation Transmission Distribution, 1997, 144(5), p. 437-444.
10. Noroozian M., Angquist L., Ghandhari M., Andersson G., Use of UPFC for optimal power flow control, IEEE Trans. Power Delivery, 1997, 12(4), p. 1629-1634.
11. Abido M. A., A novel multiobjective evolutionary algorithm for environmental/economic power dispatch, Electric Power System Research, 2003, 65(1), p. 71-81.
12. Dias A. H. F., de Vasconcelos J. A., Multi-objective genetic algorithms applied to solve optimization problems, IEEE Trans. On Magnetics, 2002, 38(2), p. 1133-1136.
13. Herrera F., Lozano M., Verdegay J. L., Tackling real-coded genetic algorithm:operators and tools for behavioural analysis, Artif. Intell. Rev, 1998, 12(4), p. 265-319.