An Integrated Approach for Non-Recursive Formulation of Connection-Coefficients of Orthogonal Functions
Monika GARG* and Lillie DEWAN
Electrical
Engineering Department, National Institute of Technology
E-mails: monika_mittalkkr@rediffmail.com (1), l_dewan@nitkkr.ac.in (2)
*Corresponding author
Abstract
In this paper, an integrated approach is proposed for non-recursive formulation of connection coefficients of different orthogonal functions in terms of a generic orthogonal function. The application of these coefficients arises when the product of two orthogonal basis functions are to be expressed in terms of single basis functions. Two significant advantages are achieved; one, the non-recursive formulations avoid memory and stack overflows in computer implementations; two, the integrated approach provides for digital hardware once-designed can be used for different functions. Computational savings achieved with the proposed non-recursive formulation vis-à-vis recursive formulation, reported in the literature so far, have been demonstrated using MATLAB PROFILER.
Keywords
Connection Coefficients; Haar Wavelet; Orthogonal Functions; Operational Matrices; Product Coefficients Matrices.
Introduction
Orthogonal functions, such as block pulse functions, Walsh functions, Legendre functions, Laguerre functions, Fourier functions and Haar functions, have been extensively used for providing piecewise constant solutions to different problems in Engineering and Sciences in terms of differential equations, analysis, optimization and identification of linear and non-linear systems.
At the first place, piecewise constant solutions are computationally more efficient and secondly, they provide the only means to obtain the solution when the relevant conventional technique fails. In this approach, known and unknown continuous time functions are expanded in terms of the relevant orthogonal basis functions and various mathematical operations like integration, differentiation, multiplication etc. are replaced by matrices resulting in matrix algebraic equations which are then solved to find the required unknown functions.
The need for computing the connection coefficients of the orthogonal functions arise when product of two orthogonal basis functions are to be expressed in terms of single basis functions.
Hitherto, the recursive formulation have been reported in the literature [1-11,15,16] which are different for different orthogonal functions. The cited advantage of recursive formulation that the order of the involved matrices are less is not of much significance in the present era of abundant cheap computing capability available at hand. The possibility of multifaceted digital-hardware seems to be better option rather. The present formulation is a step in that direction.
Moreover, recursive formulations have the following disadvantages:
1. Matrices at higher resolutions are calculated with the help of all the matrices at lower resolutions. So it becomes computationally inefficient.
2. Recursive formulations are generally avoided in computer implementations.
3. These recursive formulations are different for different orthogonal functions [1-7].
Paraskevopoulos [3,4] and Razzaghi [5] derived the relevant matrices for chebyshev series and fourier series in their own right, respectively. Improved product formula for walsh functions was proposed by Watanabe and Kawata for the LQG control design [6]. Afterwards, Hsiao et al. derived the matrix of integration for Haar wavelet [7] and proposed recursive formulations for different matrices for Haar wavelet [8]. In a number of studies, Karimi et al. [9-11] applied these recursive formulations for analysis, optimal control and robust vibration control of linear time-invariant and time-varying systems.
Lin Wu et al. [12] made
the sole effort in presenting the integrated approach for computing the
integration matrix for different orthogonal functions in terms of the generic
orthogonal function and applied it for numerical inversion of the
In [17,18] and the present paper, the work of Lin Wu et al. is further extended and an integrated approach is proposed for computing connection coefficients of orthogonal functions. The proposed non-recursive formulation is developed in terms of generic orthogonal function which is replaced by corresponding basis function for computing coefficients of a particular orthogonal function.
The paper is organized as follows: In the second section, the principle, on which the proposed method is based, is discussed. The integrated non-recursive formulation for computing connection coefficients of orthogonal functions is developed in terms of a generic orthogonal function and is presented in third section. In fourth section, connection coefficients of different orthogonal functions are computed using the generic formulation. Computational savings achieved and an application of connection coefficients is demonstrated in next section, followed by conclusions in the end.
Principle of the Proposed Method
The proposed unified method is based on the following fundamental properties of orthogonal functions in general and block pulse functions in particular:
1.
The generic orthogonal function 
can be
represented in symbolic form as
(1)
where
elements 
are the basic functions. In
numeric form, the corresponding sampled values of are
arranged as rows to form the generic orthogonal function matrix
.
2. The symbolic form of a generic
orthogonal function 
can be represented as the product
of numeric form of the function and symbolic
form of the block pulse functions 
i.e.:
(2)
where:
and
are the block functions
(3)
The 
block
function is unity over the interval 
and zero
elsewhere and in numeric form 
where 
is
Identity matrix of dimension 
.
For a
particular orthogonal function the generic function is
replaced by corresponding basis function.
Analytical non-recursive formulation for computing connection coefficients is presented in the next section.
Proposed Non-Recursive Formulation for Computing Connection Coefficients
The multiplication of
two generic orthogonal functions i.e. 
can be spanned
by corresponding basis functions. Related expansion coefficients are known as
connection coefficients, expressed as:
(4)
where 
is
the generic orthogonal function connection coefficients’ matrix of dimension 
and
are corresponding expansion
coefficients.
Using the fundamental property of orthogonal functions from (2), (4) can be expressed as:
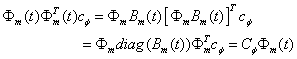(5)
where
the disjoint property of block pulse functions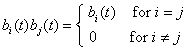 
is
used.
Eqn. (5) can
be further simplified, using (2), by expressing expansion coefficients 
in
terms of block function expansion coefficients 
as:
(6)
Simplifying (6)
after post multiplying by 
on both sides,
results in:
(7)
Substituting (7) in (5), we get:
(8)
Simplifying
(8), using the orthogonal property of the generic orthogonal function and
numeric form of the block pulse function, is
obtained as
(9)
Equation (9) is the desired non-recursive formulation for computing connection coefficients of generic orthogonal function.
The non-recursive formulation in (9) is shown to result in the connection coefficients of different orthogonal functions like Walsh, Fourier and Haar functions by using the appropriate basis functions in the next section.
Computation of Connection Coefficients for Different Orthogonal Functions using the Proposed Method
The proposed integrated
approach is applied for computing connection coefficients of different
orthogonal functions such as Walsh, Haar and Fourier functions in this section.
For demonstration purpose, the results at resolution 
are
given for the example discrete sequence consisting of four samples accordingly
and hence 
due to identity nature of block
basis functions.
Walsh Function
The kernel of discrete
Walsh transform, for 
, is defined
as:
(10)
Where 
is
the bit in the binary representation of 
.
For computing
connection coefficients of walsh functions, denoted as 
at
resolution , the corresponding
basis function from (10) are substituted in (9) in place of generic orthogonal
basis functions, resulting in:
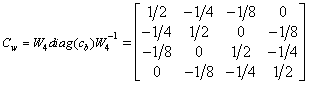(11)
It is indeed the result derived by Chen and Hsiao in their original paper [1].
Haar Function
The
orthogonal set of Haar functions 
is a group of
square waves with magnitude of ±1 in certain intervals and zeros elsewhere
[14], defined as:
(12)
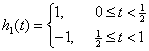(13)
All the other functions are dilations and translations of (13), according to the relation:
(14)
where 
indicate
dilations and translations respectively. The resolution m is given by:
For computing
connection coefficients of Haar functions, denoted as 
at
resolution , the corresponding basis function from
(12) & (13) are substituted in (9) in place of generic orthogonal basis
functions, resulting in:
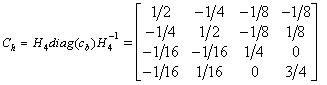(15)
The result is exactly the same as reported in [8].
Fourier Function
The basis of
Fourier Series are complex exponentials, 
,
where 
represents the harmonic
of fundamental frequency 
. Discretized version of these
continuous time complex exponentials gives the bases of Discrete Fourier
Transform which are represented by 
, where 
,
and 
is the
total number of points at which the transform is calculated [4,5].
In terms of
the orthogonal set of functions 
,
where is the resolution. The discretized
complex exponentials are then expressed as 
where 
. The 
represent
the piecewise-constant approximation of discrete orthogonal set of functions
as:
(16)
For computing
connection coefficients of Fourier functions, denoted as 
at
resolution , the corresponding
basis function from (16) are substituted in (9) in place of generic orthogonal
basis functions, resulting in
(17)
Note that since the basis of Fourier function are complex, its connection coefficients are also complex. The result in (17) is exactly same as reported in [5].
Similarly connection coefficients of other orthogonal functions, possessing sinusoidal and non-sinusoidal basis functions such as Discrete cosine functions (DCT) and Hartley functions (DHT), can also be computed by the proposed integrated approach.
Computational savings achieved via the proposed integrated non-recursive formulation for computing the connection coefficients of orthogonal functions, vis-à-vis the recursive formulation, is demonstrated in the next section for the case of Haar functions due to its nice properties of multi-resolution and compact support. State response of a linear time-variant system is also presented as an application.
Computational Savings and Application
Computational Savings
The
analytical non-recursive formulation for computing the connection coefficients
for the case of Haar functions is obtained, as in (15), for any resolution as 
.
The corresponding recursive formulation reported in the literature [8] is:
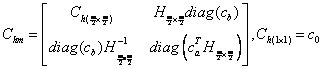
where 
, 
.
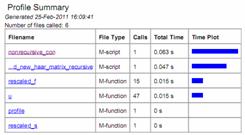
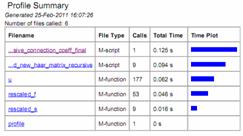
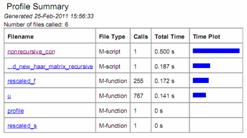
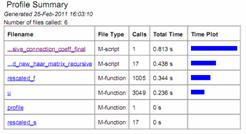
Computational savings achieved in computing connection coefficients using the proposed non-recursive formulation vis-à-vis recursive formulation is shown using MATLAB PROFILER in Table 1. The PROFILER is obtained on a PENTIUM(R) M 1.73 GHz machine for the same number of files called.
Table 1. Computational Efficiency for Proposed Integrated Non-Recursive and Existing Recursive Method: Computing Connection Coefficients of Haar Functions using Matlab Profiler
|
Resolution |
Proposed Integrated Non-recursive Approach |
Existing Recursive Approach |
|
|
|
|
|
|
|
|
It is evident from
Application
Consider a first-order linear time-variant system given as:
(18)
where 
is the
state, 
is the
input and 
is the
initial state of the system.
Comparing (18) with the generalized linear time-variant system state-space model of the following form:
(19)
we get 
and 
.
The
product of 
and 
are
simplified to be spanned by Haar basis with the help of proposed non-recursive
formulation for computing connection coefficients to obtain state response of
the system in (18).
In
Haar transform domain, the final simulation time 
is normalized
to be unity by substituting 
in
(18) where 
.
After normalization of time scale, (18) becomes:
(20)
Next each term in (18) is expanded into the Haar transform as
(21)
(22)
where 
and 
are
the expansion coefficients of 
and 
respectively.
The 
is the Haar basis.
Relation between 
and
are obtained by integrating (21)
on both sides:
(23)
Using forward operational matrix of
integration 
derived by Lin Wu et. al [12] and substituting the
expansions from (21) and (22), (23) becomes:
(24)
where initial state is
expanded in Haar domain as 
, 
.
The effect of the term , arising
out of normalization of time scale, is incorporated in .
Solving (24) for yields:
(25)
On the similar lines, the expansions
of 
,
and 
are expressed as:
(26)
(27)
(28)
where
,
and 
are the expansion coefficients of ,
and respectively.
The problem involves obtaining the state response of the system, hence Haar expansions of various functions, from (21) – (28), are substituted in (18) to obtain:
(29)
Rearranging (29) yields:
(30)
Each
of the term 
in
(30) is expressed to be spanned by Haar basis using the proposed integrated
non-recursive formulation for computing connection coefficients, which are
evaluated non-recursively in (15), as:
(31)
where 
denotes
the connection coefficients for the corresponding variables.
Right
multiplying each term in (31) by 
, we get:
(32)
Substituting
the value of from (25) and collecting the
terms results in:
(33)
is obtained from (33) as:
(34)
It
is trivial to calculate the inverse of the term 
due to
sparse nature of the matrix - a key characteristics of Haar function
[14]. The computed values of from
(34) are used to evaluate the desired values of state using
(22) for the input 
, resolution 
are
shown in Fig. 1 along with the analytical solution.
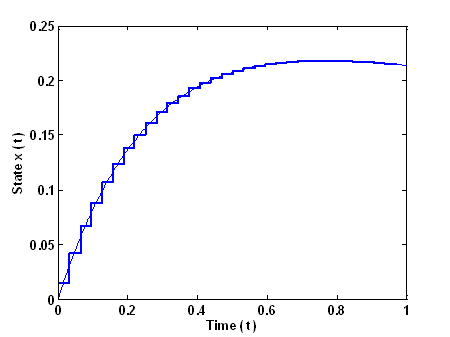
Figure 1. State response of linear time-varying system
It is evident from Fig. 1 that the state response, of the linear time-variant system, evaluated using the proposed integrated non-recursive approach, is conforming well to the analytical solution which is shown as continuous curve.
Conclusions
An integrated non-recursive formulation for computing the connection coefficients of orthogonal functions has been successfully developed and presented in terms of a generic orthogonal function. This generic formulation is then shown leading to particular cases of different orthogonal functions such as Walsh, Haar, and Fourier. The integrated scope of the proposed formulation is established by obtaining these particular instances merely by replacing the generic basis with the corresponding basis. Computational savings obtained, in using the proposed non-recursive formulation, are demonstrated with the help of MATLAB PROFILER vis-à-vis recursive formulation, reported and used in the literature so far. State response of a linear time-varying state-space system is obtained to demonstrate an application of the connection coefficients. Further computational savings can be explored by devising computationally efficient algorithms for finding the inverses of matrices involved.
References
1. Chen C.F., Hsiao C.H., A state-space approach to Walsh series solution of linear systems, Int. J. System Sci., 1965, 6(9), p. 833-858.
2. Hsu N.S., Cheng B., Analysis and optimal control of time-varying linear systems via block pulse functions, Int. J. Control, June 1981, 33(6), p. 1107-1123.
3. Paraskevopoulos P.N., Chebyshev series approach to system identification, analysis and optimal control, J. Franklin Inst., 1983, 316, p. 135-157.
4. Paraskevopoulos P.N., Sparis P.D., Mouroutsos S.G., The Fourier series operational matrix of integration, Int. J. System Sci., 1985, 16(2), p.171-176.
5. Razzaghi M., Optimal control of linear time-varying systems via Fourier Series, Journal of Optimization Theory and Applications, 1990, 65(2), p. 375-384.
6. Jin L., Watanabe A., Kawata S., The Linear-Quadratic-Gaussian Control design using an improved product formula of Walsh functions, SICE '95, July 26-28, 1995, Sapporo, p. 1375-1378.
7. Chen C.F., Hsiao C.H., Haar wavelet method for solving lumped and distributed-parameter systems, IEE Proc. Control Theory Appl., 1997, 144(1), p. 87-94.
8. Hsiao C.H., Wang W.J., Optimal control of linear time-varying systems via Haar wavelets, J. Optimization Theory Appl., 1999, 103, p. 641-655.
9. Karimi H.R., Lohmann B., Jabehdar Maralani P. and Moshiri B., A Computational Method for solving optimal control and parameter estimation of linear systems using Haar Wavelets, Int. J. of Computer Mathematics, 2004, 81(9), p. 1121-1132.
10. Karimi H.R., Lohmann B., Jabehdar Maralani P. and Moshiri B., Haar wavelet-based optimal control of time-varying state-delayed system: A computationa method, IEEE Proc. Conf. Computer Aided Control System Design, 2006, p. 1528-1533.
11. Karimi H.R., Lohmann B., A computational method to robust vibration control of vehicle engine-body system using haar wavelet, IEEE Proc. Int. Conf. Control Applications, 2006, p. 169-174.
12. Wu J.L., Chen C.H., Chen C.F., A unified derivation of operational matrices of integration for integration in system analysis, IEEE Proc. Int. Conf. on Information Technology: Coding and Computing, 2000, p. 436-442.
13. Wu J.L., Chen C.H., Chen C.F., Numerical inversion of Laplace transform using Haar wavelet operational matrices, IEEE Trans. on Circuits and Systems-Part I: Fundamental Theory and Applications, 2001, 48(1), p.120-122.
14.
15. Ordokhani Y., Numerical solution of non-linear volterra-hammerstein integral equations using the hybrid block pulse and rationalized Haar functions, Applied Mathematical Sciences, 2008, 2(51), p. 2531-2541.
16. Oishi M., Moro S., Matsumoto T., A modified method for circuit analysis using Haar wavelet transform with adaptive resolution - For circuits with waveform with sharp convex ranges, European Conf. on Circuit Theory and Design, ECCTD 2009, 2009, p. 299-302.
17. Garg M., Dewan L., A novel method of computing Haar connection coefficients for analysis of HCI systems, Proc. of Second 2nd International Conference on Intelligent Human Computer Interaction (IHCI 2010), Lecture Notes in Control and Information Sciences (LNCS), Springer-Verlag, ISBN 978-81-8489-540-7, 2010, p. 360-365.
18. Garg M. and Dewan L., A numerical method for linear ODEs using non-recursive Haar connection coefficients, International Journal of Computational Science and Mathematics (IJCSM) (Accepted).