A Mathematical Model of Complacency in HIV/AIDS Scenario: Sex-Structure Approach

 

Gbolahan BOLARIN*

 

Department of Mathematics and Statistics, Federal University of Technology, Minna, Niger State, Nigeria.

E-mail: g.bolarin@futminna.edu.ng

* Corresponding author: +234-80-33-88-31-37

 

 

Abstract

In this study we use sex-structure approach to examine the effect of complacent sexual behaviour (risky sexual activities) on the rate of infection of HIV/AIDS in a population. We partitioned the population into two classes (male and female) represented by to express our model equation as a set of differential equations. We were able to express the number of AIDS cases (male and female) as linear functions that depend on the number of AIDS patient present in the population. We were also able to determine the equilibra states of the model. We found that the Basic Reproduction Number (R0, which is the number of secondary infections due to introduction of infective into the population) of both female and male partitions of the population is given as .

Keywords

Differential equation; HIV/AIDS; Sex-Structure; Complacency; Stability; Equilibrium; Basic Reproduction Number.

 

 

Introduction

 

The issue of HIV/AIDS and other Sexually Transmitted Diseases (STD) are no longer just a national or local issue but a global one.

Complacency in this study is used to mean embarking to high risk sexual behaviours such as multiple sex partners, sex with prostitutes and non-condom use or low compliance level or incorrect use of condom when it has been discovered that HIV prevalence in a community has reduced to a very low level, with the number of AIDS cases becoming less in the community. Complacency is used in the context of a community that has registered significant decreases in HIV prevalence [4].

In this study we shall consider a sex structure model involving only male and female as sex partners i.e we shall not consider same sex interaction because that is not legal in most countries and we are considering sexual transmission since it is the principal mode of infection in most countries. To model complacency, it is assumed that behaviour change depends on the number of AIDS patients (HIV infected persons with fully blown AIDS symptoms) in the community. We shall consider three classes or compartments in our model which are, susceptibles, infectives and AIDS partitions, with population numbers in each class denoted as functions of time by Si(t), Ii(t) and Ai(t) where i = f ,m denote female and male populations, respectively. Thus, we define our sex-structured model in the context of a two-sex structure.

 

 

Material and Method

 

Model Formulation

For the purpose of this study we take the total population to be unity and so all the compartments sum up to 1.

We assume that, at any moment in time, new individuals enter the heterosexually active population at a rate, a proportion ρ (0 ≤ ρ ≤ 1) of these individuals are assumed to be female susceptibles (moved to the  class) and the complementary proportion (1 − ρ), are male susceptibles and they belong to the class.

We let  be the natural death rate for the sexually active adults. The removal rate of susceptible through infection is the number of new HIV infections per unit time. This rate is important in calculating HIV incidence which by definition is the number of new infected persons in a specified time period divided by the number of uninfected persons that were exposed for this same time period.

The rate at which an individual acquires new sexual partners (contact rate) per unit time is denoted by (). Assume that a proportion of these partners are infected male ie and at each of these sexual contacts with infectives male, a susceptible female has a probability, of getting infected. Similarly, if we assume that a proportion of these partners are infected female ie and at each of these sexual contacts with infectives female, a susceptible male has a probability, of getting infected. Let  be a function of the number of AIDS cases resulting from infection by an infected male given by  and let  be a function of the number of AIDS cases resulting from infection by an infected female given by , then the total probability of one susceptible female getting  infected from any of their sexual contacts per unit time is  and the total probability of one susceptible male getting infected from any of their sexual contacts per unit time is . The number of new HIV infected female and male per unit time are given by  and  respectively.

Upon becoming infected with HIV, female and male susceptibles enter the classes  and  of infected individuals respectively. Female and male infectives are recruited through new HIV infections described above and removed through progression to AIDS at rate  respectively and through natural death at rate . Therefore  (for ) is the duration spent in the infective stage and  is the life expectancy of the adult population. Both of these rates are assumed constant in the model.

Individual in AIDS class are recruited through progression from the infective stage to the AIDS stage and removed through AIDS accelerated deaths at rate and natural death rate and so  is the average duration spent in the AIDS stage if natural deaths are assumed constant in the model. It will be ideal to varying, since there are advances in health care there is being provided for individuals living with HIV/AIDS.

There is a constant emigration rate α > 0 of individuals to other countries except for the AIDS patients. This assumption makes the model more appropriate for Nigeria where a significant proportion of the population emigrates to developed countries for better educational facilities and in search of employment.

 

The Model Equations

From above assumptions we have the following as our model equation.

                                                                                                       (1)

The parameters  with  and the initial conditions for system (1) at time t=0 are,  for all  with  and Am(0) = Am,o > 0.

                        The Disease free Equilibrium

 

Following the approach of [2, 5, 6] the disease-free equilibrium is when the disease is not exiting the population and it is given as

 

Endemic Equilibrium

The endemic equilibrium of system (1) is given as

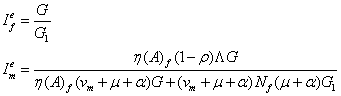
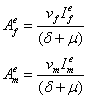
where

 

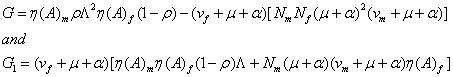
The Basic Reproduction Ratio (Number)

The basic reproduction number (the average number of secondary infection due to introduction of an infected individual into a disease free population).

Let the probability that an infected individual in the incubation period time t has survived to develop AIDS is .

Following the approach of [7,10], if a single newly infected male is allowed into the population at equilibrium, this individual will persist and infect others with probability

 at time

Therefore the number of female this individual will infect over time  will be

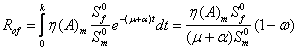
Similarly if an infected female is introduced into the population at equilibrium the number of male this individual will infect at time will be

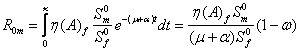
It is expected that the number secondary cases per generation due to an infected male is

 

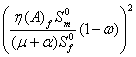
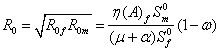
Similarly the number secondary cases per generation due to an infected female is

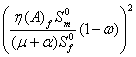
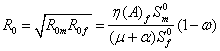
Therefore the reproduction number  is given as;

                                                                                                                                             (2)

 

Equilibrium in () plane

We will base our reasoning on the argument put forward by Baryarama et al (see [1]). Suppose at equilibrium state in (), the number of female susceptible continue to increase and hence both  and  vary. So, on setting the third equation of system (1) to zero we have;

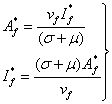                                                                                                                                       (3)

Similarly from sixth equation of system (1) we have

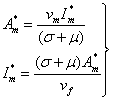                                                                                                                                       (4)

From the second equation of system (1)

Similarly from the fourth equation of system (1) we have

Now, the total population  (say) is given as;

 

Therefore, 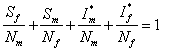, this is so because they are proportions that can only sum to unity.

Using this fact and equations (3)-(6) we have the following result;

 

 

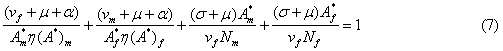
Results and Discussion

            Theorem

Suppose from (1)  Further, suppose that  as an inverse,  Then there exist tA > 0 and εA > 0 such that for all t > tA, |Af(t) - Af(tA)| < εA and |If(t) - If(A)| < εA. More so Sf(t) ® ¥ and t ® tA.

 

 

 

Proof

For convenience let and from (7) let  

So from above equation  we will obtain

 

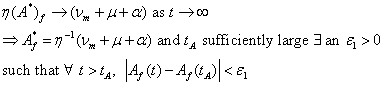
But

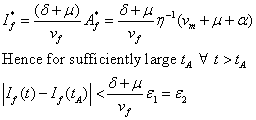
If we choose

Now, since

then

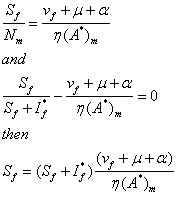
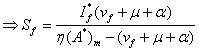                                                                                                          (8)

Since

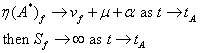
Hence the behaviour of  remains of little consequence to  since  Hence the end of prove for the second part of the theorem. From the theorem above we can express the equilibrium point in () explicitly as  (since we assumed the  is invertible) and  .

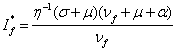More so, we can show that if  is linear, the equilibrium point in () obtained using the theorem is the same with the one obtained by direct method (see [1] for example).

 

Corollary 1

Suppose from (1)  Further, suppose that  as an inverse, Then there exist

Proof

The proof follows from theorem 1.

 

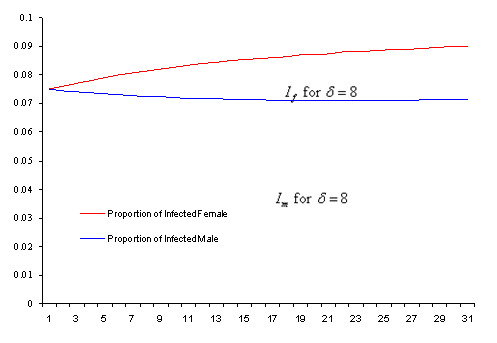
Figure 1. Time Trend of number of Infected male () and female () with Mean life time of HIV/AIDS patient = 8 years.

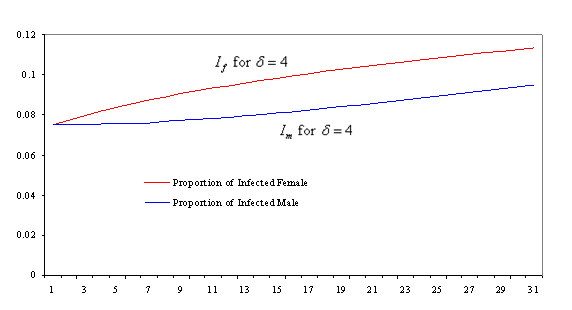
Figure 2. Time Trend of number of Infected male (Im) and female (If) with Mean life time of HIV/AIDS patients = 4 years

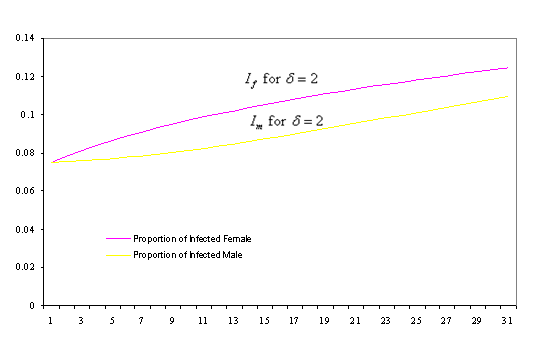
Figure 3. Time Trend of number of Infected male (Im) and female (If) with Mean life time of HIV/AIDS patient = 2 years

 

For our model we were able to show that the Basic Reproduction Number  for the female and male individuals in the population is given as  (from equation (2)). This shows that the Basic Reproductive Number of female proportion in the population due to introduction of infected male into a population is the same as the Basic Reproductive Number of male proportion due to introduction of infected female into a population.

This is similar to the study of Kamali et al (see [9]), in their article they found that there is a relationship between HIV prevalence and sexual behavioural change.

Also from figures 1-3 it could be noticed that the number of infected females in each case are more than that of males, this is due to the fact that the infectivity rate of male individual is higher than that of female (due to high concentration of the virus in sperm), this is a fact that has been alluded to by various authors; see [10].

 

 

Conclusion

 

The model formulated using sex-structure approach show that complacency could lead to high infection rate in a population. It can be seen from figures 1-3 that the lower the expected life time of HIV/AIDS patient in a population the higher the rate of infection, this is due to the fact that more people can embark on high sexual risk since there is an assumption that HIV/AIDS patients do not persist in a population for longer period.

From our findings it will be of great service to nations if the authorities in charge of prevention of HIV/AIDS can find a way to increase life expectancy of HIV/AIDS patients through treatment so has to prevent possible complacency behaviour by the populace.

 

 

Acknowledgements

I am grateful to Dr Tayo D. Olayiwola formally of Federal Medical Centre, Bida, Nigeria for his professional guidance during the conduct of this study. Also I appreciate the effort put in by the referee to review this work and for the observations and comments.

 

 

References

 

1.             Baryarama F., Luboobi L.F. and Mugisha J.Y.T., Periodicity of the HIV/AIDS Epidemic in a Mathematical Model that Incorporate Complacency, American Journal of Infectious Diseases, 2005, 1(1), p. 55-60.

2.             Doyle M.T., Greenhalgh D., Blythe S., Equilibrium analysis of a mathematical model for the spread of AIDS in a two sex population with mixing constraints, J. Biol. Syst., 1998, 6(2), p. 159–185.

3.             Fabiani M., Ble C., Grivel C., Lukwiya M., HIV-1 Prevalence Trend Among Different Risk Groups in Gulu District, North Uganda, Journal of Acquir. Immun. Defic. Syndr., 1998, 37, p. 1180-1186.

4.             Hale J.K., Ordinary Differential Equations, Wiley-Interscience, New York, 1969.

5.             Hethcote H.W, Stech H.W, van den Driessche P., Periodicity and stability in epidemic models: A survey, in Differential Equations and Applications in Ecology, Epidemics and Population Problems, Academic Press, New York, 1981, p. 65-82.

6.             Hethcote H.W., The mathematics of infectious diseases. Society for Industrial and Applied Mathematics, Siam Review, 2000, 42(4), p. 599-653.

7.             Hyman J.M., Li J., An intuitive formulation for the reproductive number for the spread of diseases in heterogeneous populations. Math. Biosci., to appear.

8.             Isham V., Medley G., Models for Infectious Human Diseases, Cambridge University Press, Cambridge, 1996.

9.             Kamali A., Carpenter L.M., Whitworth J.A.G., Pool G., Seven-year Trends in HIV-1 Infection Rates and Changes in Sexual Behaviour Among Adults in Rural Uganda. Journal of Acquir. Immun. Defic. Syndr., 2000, 14, p. 427-434.

10.         Mukandavire Z., Garira W., Age and Sex Structured Model for Assessing the Demographic Impact of Mother-to-Child Transmission of HIV/AIDS. Bulletin of Mathematical Biology, 2007, 69, p. 2061-2092.