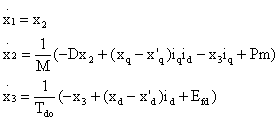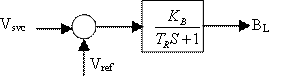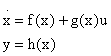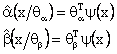Transient Stability Enhancement in Power System Using Static VAR Compensator (SVC)
Youssef MOULOUDI*, Abdellah LAOUFI and Bousmaha BOUCHIBA
Department of Electrical Engineering, Bechar University, Bechar, Algeria.
*Corresponding author E-mail: mouloudiyoussef@yahoo.fr
Abstract
In this paper, an indirect adaptive fuzzy excitation and static VAR (unit of reactive power, volt-ampere reactive) compensator (SVC) controller is proposed to enhance transient stability for the power system, which based on input-output linearization technique. A three-bus system, which contains a generator and static VAR compensator (SVC), is considered in this paper, the SVC is located at the midpoint of the transmission lines. Simulation results show that the proposed controller compared with a controller based on tradition linearization technique can enhance the transient stability of the power system under a large sudden fault, which may occur nearly at the generator bus terminal.
Keywords
Feedback linearization; SVC controller; generator excitation; indirect adaptive fuzzy.
Introduction
An interconnected power system basically consists of several essential components. They are namely the generating units, the transmission lines, the loads, the transformer, static VAR compensators and lastly the HVDC (High Voltage Direct Current) lines. During the operation of the generators, there may be some disturbances such as sustained oscillations in the speed or periodic variations in the torque that is applied to the generator. These disturbances may result in voltage or frequency fluctuation that may affect the other parts of the interconnected power system.
External factors, such as lightning, can also cause disturbances to the power system. All these disturbances are termed as faults. When a fault occurs, it causes the motor to lose synchronism if the natural frequency of oscillation coincides with the frequency of oscillation of the generators. With these factors in mind, the basic condition for a power system with stability is synchronism. Besides this condition, there are other important condition such as steady-state stability, transient stability, harmonics and disturbance, collapse of voltage and the loss of reactive power. Different approaches for excitation control are available in literature such as adaptive fuzzy excitation control of power systems based on input-output linearization technique [1], nonlinear excitation controls based on feedback linearization control (FBLC) concept [2,3], nonlinear SVC control for improving power system stability [4], and coordinated control of generator excitation and SVC [5,6]. Adaptive nonlinear excitation control for interconnected power system is reported in [7].
Stability enhancement is of great importance in power system design. Excitation control and static VAR compensator (SVC) play important roles in stability enhancement of power systems. SVCs are increasingly applied for various reasons by the utilities in modern power systems with long transmission lines and remote sources of generations. Since SVCs can achieve fast and precise regulation of terminal voltage, SVC control schemes attract increasing attention in recent years. In addition to its functions for rapid control of voltage, SVC installations serve to improve the transient stability of power system following a major disturbance to the system [8].
A three-bus system, which contains a generator and an SVC, is considered in this work. The SVC is located at the midpoint of the transmission lines. A nonlinear feedback law for the generator excitation is found which linearizes and decouples the power system model. A new coordinated excitation and SVC control scheme is proposed based on linearized model. The new coordinated controller consists of two controllers, an excitation controller and an SVC controller. The controllers for the generator excitation and SVC are designed separately based only on local measurements.
This paper presents an indirect adaptive fuzzy excitation control based on input-output linearization. The indirect adaptive control use fuzzy logic systems to model the plant and construct the controllers assuming that the fuzzy logic systems represent the true plant, therefore fuzzy IF-THEN rules describing the plant can be directly incorporated into the indirect adaptive fuzzy controller.
Material and Method
To simplify the discussion, a simplified model for a generator and an SVC system, which forms a three bus system shown in Figure 1 (Xl12=Xl23) is considered.

Figure 1. A simplified generator and SVC three bus model
Mechanical equation [1]:
|
|
(1) |
|
|
(2) |
Generator electrical dynamics. The plant model can be written as:
|
|
(4) |
where x1 = ∆δ is the relative rotor position, x2 = w is the relative speed and x3 = Eq' is the transient EMF in the quadrature axis.
The mechanical power input Pm is assumed constant and the electrical power output Pe is given by:
|
|
(5) |
|
|
(6) |
And the direct and quadrature axis currents are given by:
|
|
(7) |
and:
|
|
(8) |
Another variable of interest in power system stability
studies is the generator terminal voltage. The terminal voltage is obtained as:![]() , where
, where ![]() and
and ![]() [7,9].
[7,9].
Static VAR Compensator
The applied SVC is shown in Figure 2, which is a fixed capacitor and thyristor controlled reactor (FC/TCR) type and located at the midpoint of each transmission line. The magnitude of the SVC admittance is obtained by [10,11]:
|
|
(9) |
|
|
(10) |
According to the variations in terminal voltage and angular speed, the susceptance of the inductor BL and then BS can be regulated as shown in Figure 3 [12].
|
|
|
|
Figure 2. FC/TCR type of SVC |
Figure 3. Block diagram of the SVC controller |
The SVC dynamic model can be expressed as follows:
|
|
(11) |
Where BL(t) is the susceptance of the inductor in SVC; BC the susceptance of the capacitor in the SVC; TR the time constant of the SVC regulator, KB, the gain of the SVC regulator and uB(t) is the input of the SVC regulator.
The configuration of the SVC is shown in Figure 2, the fault we will consider in this paper is a symmetrical 3-pahse to ground short circuit fault, which accurse at the transmission lines. λ is the fraction of the faulted line to the left of the fault. If λ = 0 the fault is at the generator bus terminal. λ = 0.5 puts the fault in the middle of the line between bus 1 and bus 2, and so on.
Feedback Linearization
In this section, the design principles using the direct feedback linearization (DFL) technique to design a nonlinear coordinated controller for the power system shown in Figure 1 is considered [13].
The dynamic model given in Equation (1) can be written in the following form [7]:
|
|
(12) |
where:
|
|
|
|
|
|
![]() and
and ![]() .
.
The feedback linearizing and decoupling control is then defined as [14]:
|
|
(13) |
The expressions for α(x) and β(x) are reported in the appendix.
For tracking the output to a desired reference ym, the new input v can be chosen as:
|
|
(14) |
where e is the tracking error defined as e=(ym-y )
and a1, a2, a3 are chosen such that the
polynomial ![]() is strict
Hurwitz and the system has poles at desired locations.
is strict
Hurwitz and the system has poles at desired locations.
The control law given by Equations (13) and (14) results in feedback linearized and decoupled system with the output y converging asymptotically to the desired response.
Consider the SVC model (11) is linear, when a fault occurs, the SVC can help to enhance the stability.
Implementation of this control law requires precise information about the system parameter specifically the transmission admittance yt. However the yt is usually imprecisely modelled or may vary due to faults in the power system. The adaptive fuzzy controller designed next maintains stability and desired performance in the presence of uncertainty or unknown variation in plant parameters and structures.
Adaptive Fuzzy Control
The fuzzy logic systems with centre average defuzzifier, product-inference rule and singleton fuzzifier of the form [15]:
|
|
(15) |
where 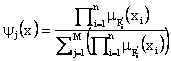
Two main reasons arise for using the fuzzy system (15) as basic building block of adaptive fuzzy controllers.
First, the fuzzy systems in the form of (15) are proven in [15] to be universal approximators, i.e., for any given real continuous function f on the compact set U, there exists a fuzzy system (15) such that it can uniformly approximate f over U to arbitrary accuracy. Therefore, the fuzzy systems (15) are qualified for modelling nonlinear systems.
Second, the fuzzy systems (15) are constructed from the fuzzy IF–THEN rules using some specific fuzzy inference, fuzzification, and defuzzification strategies. Therefore, linguistic information from a human expert can be directly incorporated into the controller [14].
According to the definition in [15], adaptive fuzzy approaches can be classified as indirect fuzzy controller and direct fuzzy controller. An indirect fuzzy controller uses fuzzy logic system as a model of the plant and can incorporate fuzzy descriptions
of the plant directly into itself. From equations (A-1) and (A-2) given in Appendix,
we can see that ![]() and
and ![]() are function of parameters E’q,
are function of parameters E’q, ![]() and w (x1, x2 and x3). These
parameters are difficult to measure, since E’q is physically unmeasurable
therefore the approximations of
and w (x1, x2 and x3). These
parameters are difficult to measure, since E’q is physically unmeasurable
therefore the approximations of ![]() and
and ![]() can be generated
using the basis function expansion as follows:
can be generated
using the basis function expansion as follows:
|
|
(16) |
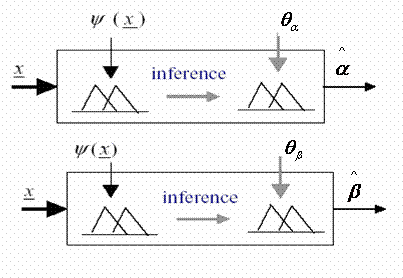
Figure 4. Structure of fuzzy systems
Using the certainly equivalent principle, the control
law (13) can be written in terms of ![]() and
and ![]() as:
as:
|
|
(17) |
where ![]() and
and ![]() with the update law for the parameters:
with the update law for the parameters:
|
|
(18) |
|
|
(19) |
The P matrix is the unique positive defined 3´3 matrix that satisfies the Lyapunov equation.
We use Lyapunov stability theory to drive controllers parameters update laws, which insure stability of the closed loop system and plant output to achieve tracking performance [1].
Results and Discussion
The studied system is illustrated in Figure 1; which applied to a real network in Algeria which contains a generator placed in the node Naama, the SVC is located at the midpoint of the transmission lines and the node Bechar. (Naama and Bechar in southwest Algerian), the parameters used in simulation are as follows:
Pm = 1, D = 5, M = 5.02, Tdo = 6.8, Xd = 2.05, X’d = 0.4, Xq = 1.46, X’q = 0.546,
δ0 = 41°, Xtrf = 0.418, Xl1 = Xl2 = 0.313, Blo = 0.7, BC = 0.7, TR = 0.02, KB = 5.
The following fault sequence is considered:
Stage 1: the system is in a per fault steady-state.
Stage 2: A fault occurs at t = 10 sec.
Stage 3: the fault is removed by opening the breakers of the faulted lines at t = 10.1 sec.
Stage 4: the transmission lines are restored with the fault cleared at t = 12 sec.
Stage 5: the system is in a post fault-state.
We have started the simulation by introducing the
feedback linearization control to enhance transient stability for a power
system. The response of the power angle under different fault location (![]() =0.5, 0.1, 0.08
and 0.05) are given in Figure 5.
=0.5, 0.1, 0.08
and 0.05) are given in Figure 5.
From the result we can see that since the physical limit
of the FDL, when the fault occurs close to the generator terminal (![]() =0.05) the
system cannot maintain the synchronism.
=0.05) the
system cannot maintain the synchronism.
When a large fault occurs, it is very difficult for FDL to adapt the variations in reactance of the transmission lines. For this reason the SVC is taken into consideration, the SVC is located at the midpoint of the transmission line in a power system. The proposed coordinated controller consists of two controllers, a generator excitation and SVC controller.
The response of the reactive power angle (![]() ) with coordinated controller, is given in Figure 6 where the fault
is located nearly at the terminal of the generator bus (
) with coordinated controller, is given in Figure 6 where the fault
is located nearly at the terminal of the generator bus (![]() ).
).
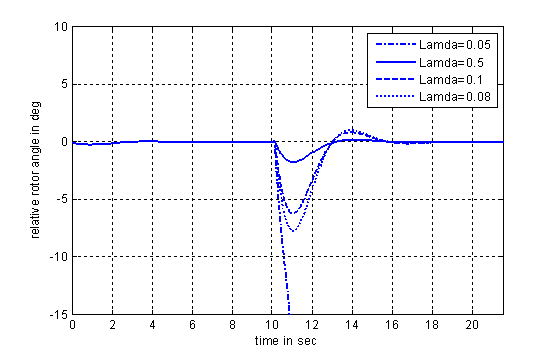
Figure 5. The response of power
angle at (![]() =0.5,
0.1, 0.08 and 0.05)
=0.5,
0.1, 0.08 and 0.05)
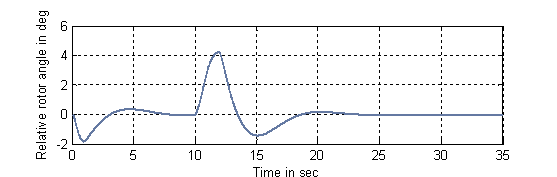
Figure 6. The response of power
angle at (![]() )
)
The simulation result shows that the proposed controller can enhance the transient stability of the power system, under a large sudden fault, which may occur nearly at the generator bus terminal, but local measurements are required.
This work presents an indirect adaptive fuzzy excitation control based on input-output linearization. In indirect adaptive control, the parameters of the plant are estimated and the controller is chosen assuming that the estimated parameters represent the true values of the plant parameters.
The comparison of the response of the relative power
angle (![]() ) under the case
coordinated control with and without indirect adaptive fuzzy controller is
given in Figure 7.
) under the case
coordinated control with and without indirect adaptive fuzzy controller is
given in Figure 7.
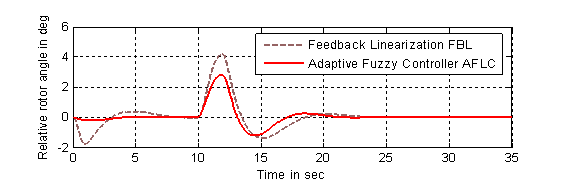
Figure 7. Response of the
relative power angle (![]() ): (1) with adaptive fuzzy controller,
(2) without fuzzy at (
): (1) with adaptive fuzzy controller,
(2) without fuzzy at (![]() )
)
The responses of the relative rotor speed (w(t)) and the
generator bus terminal voltage (Vt(t)) under the case with indirect
adaptive fuzzy controller are given in Figures 8 and 9, where the fault is
located at (![]() ). The steady-state terminal voltage is a function of the reference
operating point. Thus the terminal voltage can be brought to an acceptable
limit by moving the operating point, once the system has settled to a
steady-state operation.
). The steady-state terminal voltage is a function of the reference
operating point. Thus the terminal voltage can be brought to an acceptable
limit by moving the operating point, once the system has settled to a
steady-state operation.
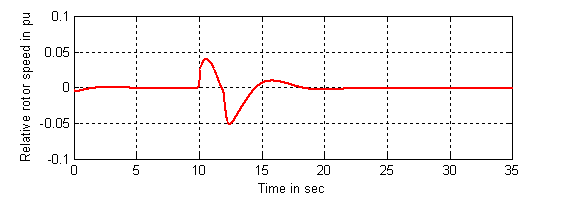
Figure 8. Response of the
relative rotor speed (w(t)) with adaptive fuzzy controller at (![]() )
)
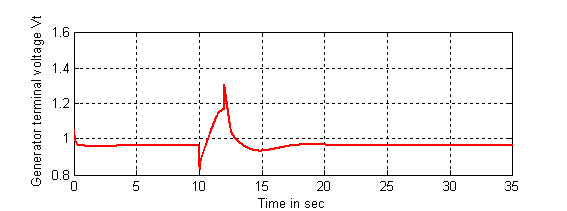
Figure 9. Response of the generator bus terminal voltage (V(t))
The response of the voltage at SVC, the reactance controlled by the SVC (BL(t)) and the response of electric power (Pe) for the system using indirect adaptive fuzzy controller are shown in Figures 10 to 14.
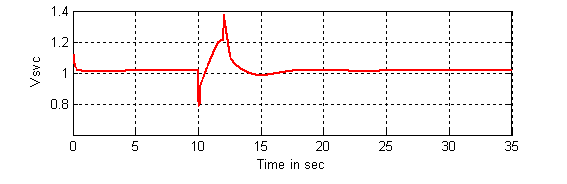
Figure 10. Response of the voltage (Vsvc(t)) at SVC
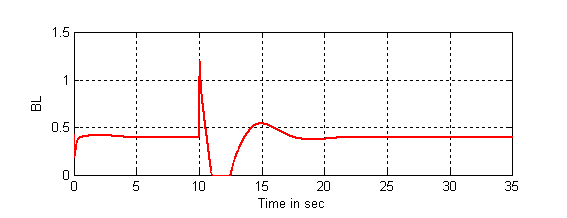
Figure 11. Response of the (BL(t))
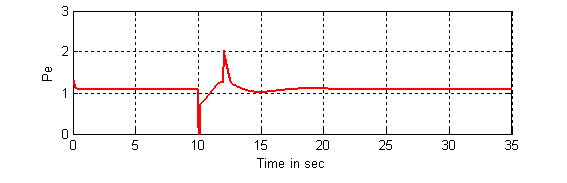
Figure 12. Response of the electric power (Pe)
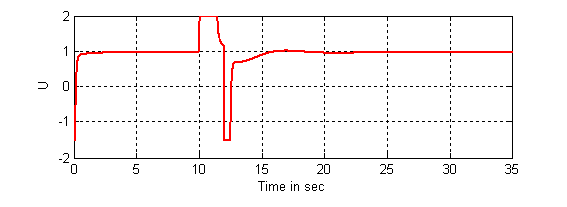
Figure 13. The input control using indirect adaptive fuzzy controller
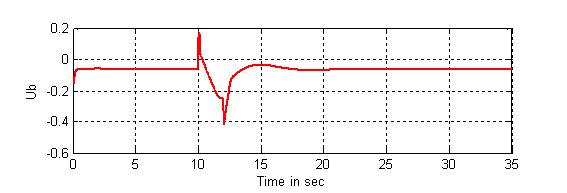
Figure 14. The input of the SVC
Conclusions
In this paper, the dynamic interaction between the generator excitation and the SVC is taken into account in the controller design. It presents an application of adaptive fuzzy control to design a non linear exciter for a power system to enhance its performance when subjected to abnormalities such as three-phase to ground faults. The proposed indirect adaptive fuzzy control is based on input-output linearization.
Simulation results show that the proposed controller can enhance transient stability of the power system under a large sudden fault, even in the case where a fault occurs nearly at the generator bus terminal.
References
3. Mak F.K., Design of nonlinear generator excitations using differential geometric control theories, in Pro. 31th Conference on Decision and Control, Tucson, AZ, Dec. 1992, p. 1149-1153.
4. Ma Y., Chen S., A study on nonlinear SVC control for improving power system stability, IEEE TENCON 93 / Beijing 1993, China, p 166-169.
6. Mahran A.R., Hogg B.W., Coordinated control of synchronous generator excitation and Static VAR Compensator, IEEE Transactions on Energy Conversion, 1992, 7(4), p 615-622.
9. Anderson P.M., Fouad A.A., Power system control and stability, Iowa State University Press, Ames, Iowa, 1977.
12. Milano F., Power System Analysis Toolbox, Documentation for PSAT version 1.0.1, January 16, 2003.
13. Li S., Applied nonlinear control, USA, Prentice-Hall, 1991.
15. Wang L.X., Fuzzy system and control, design and stability analysis, Englewood cliffs, NJ: Prentice Hall, 1991.
Appendix
The expressions
for ![]() and
and
![]() are:
are:
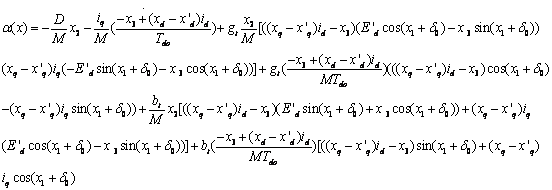 (A-1)
(A-1)
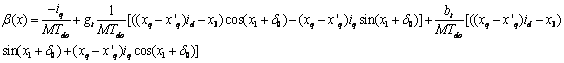 (A-2)
(A-2)
List of Symbols