A Mathematical Model of Complacency in HIV/AIDS Scenario: Sex-Structure Approach
Gbolahan BOLARIN*
Department of Mathematics and Statistics, Federal University of Technology, Minna, Niger State, Nigeria.
E-mail: g.bolarin@futminna.edu.ng
* Corresponding author: +234-80-33-88-31-37
Abstract
In this study we use sex-structure
approach to examine the effect of complacent sexual behaviour (risky sexual
activities) on the rate of infection of HIV/AIDS in a population. We
partitioned the population into two classes (male and female) represented by ![]() to express
our model equation as a set of differential equations. We were able to express
the number of AIDS cases (male and female) as linear functions that depend on
the number of AIDS patient present in the population. We were also able to
determine the equilibra states of the model. We found that the Basic
Reproduction Number (R0, which is the number of secondary
infections due to introduction of infective into the population) of both female
and male partitions of the population is given as
to express
our model equation as a set of differential equations. We were able to express
the number of AIDS cases (male and female) as linear functions that depend on
the number of AIDS patient present in the population. We were also able to
determine the equilibra states of the model. We found that the Basic
Reproduction Number (R0, which is the number of secondary
infections due to introduction of infective into the population) of both female
and male partitions of the population is given as ![]() .
.
Keywords
Differential equation; HIV/AIDS; Sex-Structure; Complacency; Stability; Equilibrium; Basic Reproduction Number.
Introduction
The issue of HIV/AIDS and other Sexually Transmitted Diseases (STD) are no longer just a national or local issue but a global one.
Complacency in this study is used to mean embarking to high risk sexual behaviours such as multiple sex partners, sex with prostitutes and non-condom use or low compliance level or incorrect use of condom when it has been discovered that HIV prevalence in a community has reduced to a very low level, with the number of AIDS cases becoming less in the community. Complacency is used in the context of a community that has registered significant decreases in HIV prevalence [4].
In this study we shall consider a sex structure model involving only male and female as sex partners i.e we shall not consider same sex interaction because that is not legal in most countries and we are considering sexual transmission since it is the principal mode of infection in most countries. To model complacency, it is assumed that behaviour change depends on the number of AIDS patients (HIV infected persons with fully blown AIDS symptoms) in the community. We shall consider three classes or compartments in our model which are, susceptibles, infectives and AIDS partitions, with population numbers in each class denoted as functions of time by Si(t), Ii(t) and Ai(t) where i = f ,m denote female and male populations, respectively. Thus, we define our sex-structured model in the context of a two-sex structure.
Material and Method
Model Formulation
For the purpose of this study we take the total population to be unity and so all the compartments sum up to 1.
We assume that, at any moment in
time, new individuals enter the heterosexually active population at a rate![]() , a
proportion ρ (0 ≤ ρ ≤ 1) of these
individuals are assumed to be female susceptibles (moved to the
, a
proportion ρ (0 ≤ ρ ≤ 1) of these
individuals are assumed to be female susceptibles (moved to the ![]() class)
and the complementary proportion (1 − ρ), are male susceptibles
and they belong to the
class)
and the complementary proportion (1 − ρ), are male susceptibles
and they belong to the ![]() class.
class.
We let ![]() be the natural
death rate for the sexually active adults. The removal rate of susceptible
through infection is the number of new HIV infections per unit time. This rate
is important in calculating HIV incidence which by definition is the number of
new infected persons in a specified time period divided by the number of
uninfected persons that were exposed for this same time period.
be the natural
death rate for the sexually active adults. The removal rate of susceptible
through infection is the number of new HIV infections per unit time. This rate
is important in calculating HIV incidence which by definition is the number of
new infected persons in a specified time period divided by the number of
uninfected persons that were exposed for this same time period.
The rate at
which an individual acquires new sexual partners (contact rate) per unit time
is denoted by ![]() (
(![]() ). Assume that a proportion of these
partners are infected male ie
). Assume that a proportion of these
partners are infected male ie ![]() and at each of
these sexual contacts with infectives male, a susceptible female has a
probability,
and at each of
these sexual contacts with infectives male, a susceptible female has a
probability, ![]() of getting infected. Similarly, if we assume that a proportion of these partners are
infected female ie
of getting infected. Similarly, if we assume that a proportion of these partners are
infected female ie ![]() and at each of these sexual
contacts with infectives female, a susceptible male has a probability,
and at each of these sexual
contacts with infectives female, a susceptible male has a probability, ![]() of getting
infected. Let
of getting
infected. Let ![]() be a function of the number of
AIDS cases resulting from infection by an infected male given by
be a function of the number of
AIDS cases resulting from infection by an infected male given by ![]() and let
and let ![]() be a
function of the number of AIDS cases resulting from infection by an infected
female given by
be a
function of the number of AIDS cases resulting from infection by an infected
female given by ![]() , then the total probability of one
susceptible female getting infected from any of their sexual contacts per unit
time is
, then the total probability of one
susceptible female getting infected from any of their sexual contacts per unit
time is ![]() and
the total probability of one susceptible male getting infected from any of
their sexual contacts per unit time is
and
the total probability of one susceptible male getting infected from any of
their sexual contacts per unit time is ![]() . The number of new HIV infected female
and male per unit time are given by
. The number of new HIV infected female
and male per unit time are given by ![]() and
and ![]() respectively.
respectively.
Upon becoming
infected with HIV, female and male susceptibles enter the classes ![]() and
and ![]() of
infected individuals respectively. Female and male infectives
are recruited through new HIV infections described above and removed through
progression to AIDS at rate
of
infected individuals respectively. Female and male infectives
are recruited through new HIV infections described above and removed through
progression to AIDS at rate ![]() respectively and through natural
death at rate
respectively and through natural
death at rate ![]() . Therefore
. Therefore ![]() (for
(for ![]() ) is
the duration spent in the infective stage and
) is
the duration spent in the infective stage and ![]() is the life expectancy
of the adult population. Both of these rates are assumed constant in the model.
is the life expectancy
of the adult population. Both of these rates are assumed constant in the model.
Individual in AIDS class are
recruited through progression from the infective stage to the AIDS stage and
removed through AIDS accelerated deaths at rate ![]() and natural death rate
and natural death rate ![]() and so
and so ![]() is the
average duration spent in the AIDS stage if natural deaths are assumed constant
in the model. It will be ideal to varying
is the
average duration spent in the AIDS stage if natural deaths are assumed constant
in the model. It will be ideal to varying![]() , since there are advances in health
care there is being provided for individuals living with HIV/AIDS.
, since there are advances in health
care there is being provided for individuals living with HIV/AIDS.
There is a constant emigration rate α > 0 of individuals to other countries except for the AIDS patients. This assumption makes the model more appropriate for Nigeria where a significant proportion of the population emigrates to developed countries for better educational facilities and in search of employment.
The Model Equations
From above assumptions we have the following as our model equation.
![]()
![]()
![]() (1)
(1)
![]()
![]()
![]()
The parameters ![]() with
with ![]() and the initial conditions for system (1) at
time t=0 are,
and the initial conditions for system (1) at
time t=0 are, ![]() for all
for all ![]() with
with ![]() and Am(0)
= Am,o > 0.
and Am(0)
= Am,o > 0.
The Disease free Equilibrium
Following the approach of [2, 5, 6] the disease-free equilibrium is when the disease is not exiting the population and it is given as
![]()
Endemic Equilibrium
The endemic equilibrium of system (1) is given as
![]()
![]()
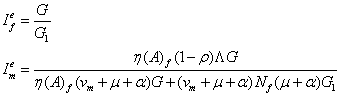
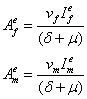
where
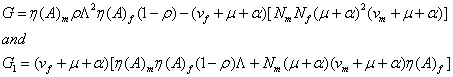
The Basic Reproduction Ratio (Number)
The basic reproduction number ![]() (the average number of secondary infection due to introduction of an
infected individual into a disease free population).
(the average number of secondary infection due to introduction of an
infected individual into a disease free population).
Let the probability that an infected individual in the
incubation period time t has survived to develop AIDS is ![]() .
.
Following the approach of [7,10], if a single newly infected male is allowed into the population at equilibrium, this individual will persist and infect others with probability
![]() at time
at time ![]()
![]()
Therefore the number of female this individual will
infect over time ![]() will be
will be
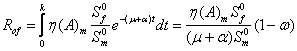
Similarly if an infected female is introduced into the
population at equilibrium the number of male this individual will infect at
time ![]() will
be
will
be
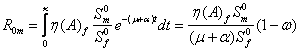
It is expected that the number secondary cases per generation due to an infected male is
![]()
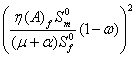
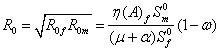
Similarly the number secondary cases per generation due to an infected female is
![]()
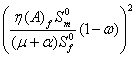
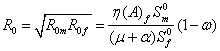
Therefore the reproduction number ![]() is given as;
is given as;
![]() (2)
(2)
Equilibrium in (![]() ) plane
) plane
We will base our reasoning on the argument put forward
by Baryarama et al (see [1]). Suppose at equilibrium state in (![]() ),
the number of female susceptible continue to increase and hence both
),
the number of female susceptible continue to increase and hence both ![]() and
and ![]() vary. So,
on setting the third equation of system (1) to zero we have;
vary. So,
on setting the third equation of system (1) to zero we have;
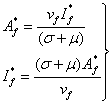 (3)
(3)
Similarly from sixth equation of system (1) we have
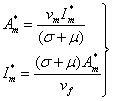 (4)
(4)
From the second equation of system (1)
![]()
Similarly from the fourth equation of system (1) we have
![]()
Now, the total population ![]() (say) is given as;
(say) is given as;
![]()
Therefore, 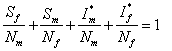 , this is so because they are
proportions that can only sum to unity.
, this is so because they are
proportions that can only sum to unity.
Using this fact and equations (3)-(6) we have the following result;
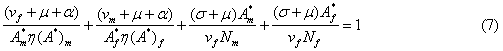
Results and Discussion
Theorem
Suppose from (1)
![]() Further,
suppose that
Further,
suppose that ![]() as an inverse,
as an inverse, ![]() Then there exist tA
> 0 and εA > 0 such that for all t > tA, |Af(t)
- Af(tA)| < εA and |If(t) -
If(A)| < εA. More so Sf(t) ® ¥ and t ® tA.
Then there exist tA
> 0 and εA > 0 such that for all t > tA, |Af(t)
- Af(tA)| < εA and |If(t) -
If(A)| < εA. More so Sf(t) ® ¥ and t ® tA.
Proof
For convenience let ![]() and from (7) let
and from (7) let ![]()
So from above equation ![]() we will obtain
we will obtain
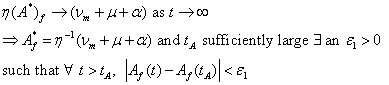
But
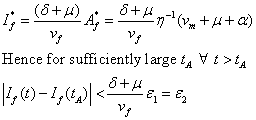
If we choose ![]()
Now, since ![]()
then
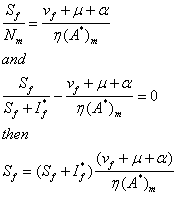
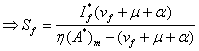 (8)
(8)
Since
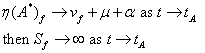
Hence the behaviour of ![]() remains of little consequence to
remains of little consequence to ![]() since
since ![]() Hence the
end of prove for the second part of the theorem.
Hence the
end of prove for the second part of the theorem.![]() From the theorem above we can
express the equilibrium point in (
From the theorem above we can
express the equilibrium point in (![]() ) explicitly as
) explicitly as ![]() (since we
assumed the
(since we
assumed the ![]() is invertible) and
is invertible) and 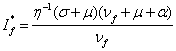 .
.
More so, we can show that if ![]() is linear, the
equilibrium point in (
is linear, the
equilibrium point in (![]() ) obtained using the theorem is
the same with the one obtained by direct method (see [1] for example).
) obtained using the theorem is
the same with the one obtained by direct method (see [1] for example).
Corollary 1
Suppose from (1) ![]() Further, suppose that
Further, suppose that ![]() as an
inverse,
as an
inverse, ![]() Then
there exist
Then
there exist ![]()
![]()
Proof
The proof follows from theorem 1.
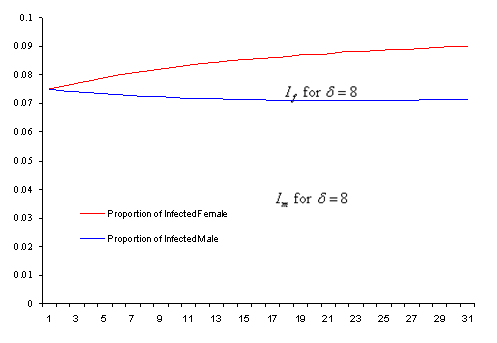
Figure 1. Time Trend of number of
Infected male (![]() ) and female (
) and female (![]() ) with Mean life time
of HIV/AIDS patient = 8 years.
) with Mean life time
of HIV/AIDS patient = 8 years.
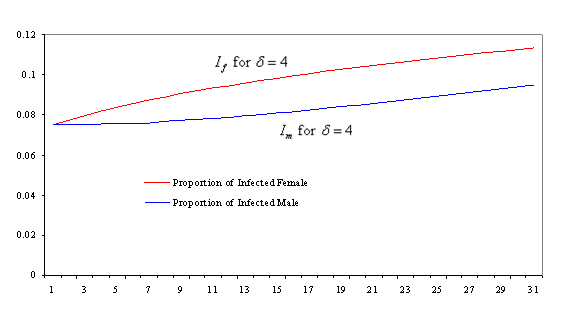
Figure 2. Time Trend of number of Infected male (Im) and female (If) with Mean life time of HIV/AIDS patients = 4 years
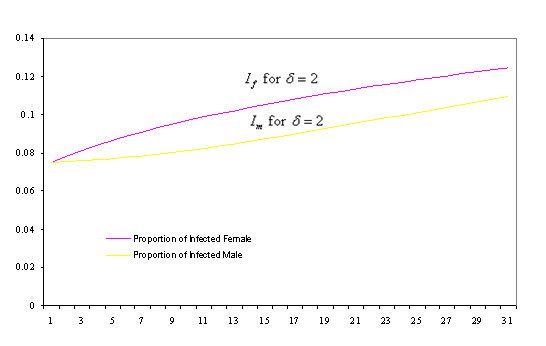
Figure 3. Time Trend of number of Infected male (Im) and female (If) with Mean life time of HIV/AIDS patient = 2 years
For our model we were able to show that the Basic
Reproduction Number ![]() for the female and male individuals in
the population is given as
for the female and male individuals in
the population is given as ![]() (from equation (2)). This shows that
the Basic Reproductive Number of female proportion in the population due to
introduction of infected male into a population is the same as the Basic
Reproductive Number of male proportion due to introduction of infected female
into a population.
(from equation (2)). This shows that
the Basic Reproductive Number of female proportion in the population due to
introduction of infected male into a population is the same as the Basic
Reproductive Number of male proportion due to introduction of infected female
into a population.
This is similar to the study of Kamali et al (see [9]), in their article they found that there is a relationship between HIV prevalence and sexual behavioural change.
Also from figures 1-3 it could be noticed that the number of infected females in each case are more than that of males, this is due to the fact that the infectivity rate of male individual is higher than that of female (due to high concentration of the virus in sperm), this is a fact that has been alluded to by various authors; see [10].
Conclusion
The model formulated using sex-structure approach show that complacency could lead to high infection rate in a population. It can be seen from figures 1-3 that the lower the expected life time of HIV/AIDS patient in a population the higher the rate of infection, this is due to the fact that more people can embark on high sexual risk since there is an assumption that HIV/AIDS patients do not persist in a population for longer period.
From our findings it will be of great service to nations if the authorities in charge of prevention of HIV/AIDS can find a way to increase life expectancy of HIV/AIDS patients through treatment so has to prevent possible complacency behaviour by the populace.
Acknowledgements
I am grateful to Dr Tayo D. Olayiwola formally of Federal Medical Centre, Bida, Nigeria for his professional guidance during the conduct of this study. Also I appreciate the effort put in by the referee to review this work and for the observations and comments.
References
1. Baryarama F., Luboobi L.F. and Mugisha J.Y.T., Periodicity of the HIV/AIDS Epidemic in a Mathematical Model that Incorporate Complacency, American Journal of Infectious Diseases, 2005, 1(1), p. 55-60.
2. Doyle M.T., Greenhalgh D., Blythe S., Equilibrium analysis of a mathematical model for the spread of AIDS in a two sex population with mixing constraints, J. Biol. Syst., 1998, 6(2), p. 159–185.
3. Fabiani M., Ble C., Grivel C., Lukwiya M., HIV-1 Prevalence Trend Among Different Risk Groups in Gulu District, North Uganda, Journal of Acquir. Immun. Defic. Syndr., 1998, 37, p. 1180-1186.
4. Hale J.K., Ordinary Differential Equations, Wiley-Interscience, New York, 1969.
5. Hethcote H.W, Stech H.W, van den Driessche P., Periodicity and stability in epidemic models: A survey, in Differential Equations and Applications in Ecology, Epidemics and Population Problems, Academic Press, New York, 1981, p. 65-82.
6. Hethcote H.W., The mathematics of infectious diseases. Society for Industrial and Applied Mathematics, Siam Review, 2000, 42(4), p. 599-653.
7. Hyman J.M., Li J., An intuitive formulation for the reproductive number for the spread of diseases in heterogeneous populations. Math. Biosci., to appear.
8. Isham V., Medley G., Models for Infectious Human Diseases, Cambridge University Press, Cambridge, 1996.
9. Kamali A., Carpenter L.M., Whitworth J.A.G., Pool G., Seven-year Trends in HIV-1 Infection Rates and Changes in Sexual Behaviour Among Adults in Rural Uganda. Journal of Acquir. Immun. Defic. Syndr., 2000, 14, p. 427-434.
10. Mukandavire Z., Garira W., Age and Sex Structured Model for Assessing the Demographic Impact of Mother-to-Child Transmission of HIV/AIDS. Bulletin of Mathematical Biology, 2007, 69, p. 2061-2092.